CAPITULO QUINTO

 

CONSTRUCTIVISMO LOGICO-HISTORICO:

LA VERDAD MATEMATICA

 

 

Como ya quedó anunciado en la introducción de esta tesis, el problema de la verdad matemática nos sitúa en la "médula" misma de la filosofía de la matemática. Esa prefiguración la constituía por un lado la afirmación que el joven Zubiri hiciera en su tesis doctoral: "[La verdad es] centro de gravitación de todo el pensamiento filosófico"[1] ; y por otro lado la afirmación de Brunschvicg:

"En el momento actual la tarea de la filosofía consiste en organizar, alrededor de la ciencia positiva, una noción positiva de la verdad; y esta tarea debe ser retomada por la base, por el estudio de los problemas que conciernen a la ciencia elemental, es decir a la matemática"[2]

Estas palabras de Brunschvicg abren un programa de investigación: definir una noción positiva de verdad alrededor de la ciencia, y una dirección de búsqueda intelectiva: acometer esta tarea desde la ciencia más elemental, es decir la matemática. Zubiri, en el inicio mismo de su investigación filosófica, toma conciencia de este programa y de su dirección precisa, haciéndolo suyo de tal modo que su obra de madurez, la Trilogía sobre la intelección, viene a ser una respuesta acabada a dicho problema. En efecto, ahí nos ofrece el autor una profunda reflexión sobre el problema de la verdad en la matemática, en la ciencia, en el conocimiento racional y en la intelección. Con esta concatenación de ámbitos, (en la que cada uno se subsume en el siguiente), queremos indicar que la reflexión de Zubiri pudo empezar por la ciencia más elemental: la matemática. Sin duda, ella está en la base de todas sus consideraciones "noológicas". Si vamos a ver cómo define el autor cuestiones claves que giran en torno al problema de la verdad —como son: certeza, rigor, exactitud, evidencia, adecuación, necesidad y universalidad, etc.—, nos encontramos con referencias explícitas a la verdad matemática. Tal es así, que podemos decir que si bien el orden de exposición de la Trilogía de la intelección es desde la intelección a su concreción en la ciencia y en la matemática, el orden de investigación originaria sería el inverso. Esta es nuestra aportación: el problema de la verdad matemática juega un papel crucial en la génesis de la noología zubiriana.

En el problema de la verdad convergen las concepciones del conocimiento matemático y de la naturaleza del objeto. Por consiguiente de la solución a este problema crucial de la epistemología matemática, —perfectamente articulado dentro de una epistemología general y de la "noología"—pende, en gran parte, la valoración que nos merezca la original aportación zubiriana a la filosofía de la matemática: el constructivismo sentiente y transcendental (según atendamos al aspecto epistemológico u ontológico, ambos son congéneres). También anticipamos en nuestra introducción general la importancia que tiene la solución del problema de la verdad matemática en la valoración de la filosofía de la matemática de un autor, lo hacíamos con las palabras de Brunschvicg:

"...si se pide a la inteligencia de la matemática definir un nuevo tipo de conexión entre la deducción racional y el contenido de la experiencia, es decir, un nuevo tipo de verdad, hallamos en la Crítica una filosofía de la matemática que señala una fecha decisiva en la historia del pensamiento humano" [3]

Ahora bien, el planteamiento que hace Brunschvicg, dada la complejidad actual del problema de la verdad matemática, no es suficiente. No basta con definir un nuevo tipo de conexión entre deducción racional y contenido de la experiencia, para que tengamos una nueva concepción de la verdad matemática. Actualmente constituyen un profundo debate las cuestiones sobre la verdad matemática: ¿creación o descubrimiento?, ¿lógica o histórica? Vemos, pues, que es preciso además definir el tipo de conexión entre descubrimiento y creación, entre lógica e historia. De este modo completamos la tesis de Brunschvicg con la nuestra propia (que defenderemos a lo largo de este capítulo): si se pide a la inteligencia matemática definir un nuevo tipo de verdad, esto es, un nuevo tipo de conexión entre deducción racional y contenido de experiencia, entre creación y descubrimiento, entre lógica e historia, hallamos en la Trilogía sobre la intelección una filosofía de la matemática que marca un hito en la historia del pensamiento humano, de fecundidad mayor que la filosofía de la matemática de la Crítica de Kant.

En la época de Kant, la historia no constituye una cuestión capital, y esto lo acusará el autor en su modo "ahistórico" de plantear el problema de la verdad matemática. Como las coordenadas que se le ofrecen en discrepancia son razón (del racionalismo) y experiencia (del empirismo), se debate con ellas hasta alumbrar una conexión entre ambas. De ahí la novedad de su concepción de la matemática, no es meramente conceptual o lógica sino también intuitiva. No nos cabe duda de que si Kant hubiera sido de nuestro tiempo se habría debatido con las nociones de lógica y de historia, y lo mismo entre descubrimiento y creación, hasta establecer un nuevo tipo de conexión entre ellas. Esto le ocurre a Zubiri, su horizonte intelectual (las geometrías no-euclídeas, el Teorema de Gödel, etc.) le fuerza inexorablemente a concebir un nuevo tipo de unidad entre lógica e historia, y entre descubrimiento y creación, que lleva, a su vez, a redefinir con nueva luz la relación entre razón y experiencia.

Zubiri penetra hondamente en este problema y no le satisface ninguna solución disyuntiva. No comparte la opinión de los autores que defienden la matemática como libre creación y producto histórico, pero que niegan su carácter de descubrimiento, de certeza y verdad, y dejan paso a la falibilidad desfundamentadora del conocimiento matemático. Igualmente rechaza la postura de los autores que defienden la matemática como un descubrimiento, atribuyéndole un carácter lógico y de verdad eterna, mas a costa de privarle del carácter histórico y de libre construcción. Podríamos pensar, pues, que el autor aporta una solución conjuntiva[4] o sintética, lo cual no supondría ninguna novedad en el panorama actual de la filosofía de la matemática, y en tal caso ¿en qué estriba su aportación, que hemos señalado como un hito? La solución del constructivismo sentiente y transcendental, como se verá, hay que precisarla en la dirección en la que se establece esta unidad y el carácter esencial de la misma. El tema no puede ser de mayor interés dentro del panorama de la actual filosofía de la matemática.

En la últimas décadas se ha escrito mucho sobre la verdad matemática. Y sin embargo, a nuestro entender, la luz sobre este tema no es mucha. Pensamos que sólo una nueva concepción de inteligencia, de realidad, y, a partir de ellas, de lógica y de historia, de creación y de descubrimiento, permitirá alumbrar una nueva noción de verdad matemática. Su luz se expandirá asimismo a las nociones de certeza, rigor, exactitud y evidencia, vinculadas a la noción de verdad. A estas rivalidades se les viene denominando "nudos" epistemológicos por su aparente dificultad insoluble. Y puede ser que así sea desde una filosofía de la matemática concipiente, sin embargo, nos preguntamos: ¿desde el constructivismo sentiente y transcendental, no serán estos "nudos", más que dificultades insolubles, unidades indisolubles? Este carácter unitario de lógica e historia, y de creación y descubrimiento, nos lleva en este capítulo de la verdad matemática a denominar el nuevo constructivismo matemático de Zubiri: Constructivismo lógico-histórico. Esta es la tercera determinación que completa las anteriores: sentiente y transcendental. Así pues, al concluir este capítulo tendremos trazado completamente el nuevo constructivismo matemático. Sus tres caracteres sentiente (intelección), transcendental (objeto) y lógico-históricoc(verdad), están intrínsecamente unidos. De ahí que el presente capítulo se entienda desde los dos anteriores.

La aportación zubiriana, en este punto, es sumamente actual y, a la vez, clásica, en cuanto que arroja una nueva luz en una dirección que nos permite "experienciar" sus resultados de un modo enriquecedor. De ahí nuestro interés en la concepción zubiriana de la verdad matemática.

 

 

1 Teorema de Gödel y la verdad matemática

 

El Teorema de Gödel abre una nueva crisis del fundamento matemático que pone en grave peligro la noción de verdad matemática. Esta conmoción de la verdad matemática, cimiento de todo el saber matemático, pone a matemáticos y filósofos de la matemática en la encrucijada de decidir si es posible el conocimiento matemático o hay que sustituir esta pretensión por la continua conjetura. El Teorema de Gödel arroja un resultado unánime: La verdad matemática no es pura consistencia formal o deducibilidad que lleva a dotarla de un carácter apodíctico, de absoluta certeza, a priori. Los resultados matemáticos se presentan a la luz de dicho Teorema como falibles, provisionales y aproximados, como lo son los resultados de las ciencias naturales. Así pues, el dogmatismo matemático defendido anteriormente es inviable, esto es, la infalibilidad matemática es un sueño de la razón, no hay un conocimiento adecuado en la matemática. Ahora bien, ¿cómo evitar el escepticismo matemático? Esta es la cuestión.

En este punto nos interesa contrastar la postura de Zubiri con la del matemático y filósofo de la matemática Lakatos. En ambos el Teorema de Gödel juega un papel crucial, les conduce, en cierto modo, a emprender direcciones de pensamiento que, si bien coinciden en su punto de arranque, divergen a lo largo de su desarrollo. En Lakatos supone la sustitución de la certeza absoluta o infalibilidad de la matemática por la falibilidad, y el abandono de la tarea de la fundamentación de la matemática. En Zubiri significa el giro desde su primera concepción de la verdad deductiva, "a priori", apodíctica, infalible de la matemática, a la adopción de la verdad empírica, dependiente de la realidad, y aproximada o parcialmente inadecuada de la matemática; esto conlleva la limitación del conocimiento matemático, pero no, como pretende Lakatos, su imposibilidad.

Una vez expuesta la significación del Teorema de Gödel en Lakatos y en Zubiri, confrontaremos las dos alternativas a la Teoría de la Verdad como Coherencia formal: falibilidad y conjetura continua, o aproximación aspectual a la realidad matemática y conocimiento matemático. Lakatos presenta el primer disyunto y Zubiri el segundo. Esto no es del todo exacto, porque, en cierto modo, veremos que la postura de Zubiri asume la falibilidad y la conjetura continua en su concepción de la verdad matemática como parcial inadecuación, pero desde un nuevo fundamento: la realidad transcendental. Ello le impedirá caer en el escepticismo, que en el caso de Lakatos nos parece inevitable.

Exponemos en primer lugar la interpretación del Teorema de Gödel que hace Lakatos desde el falibilismo crítico de la matemática, y seguidamente la interpretación zubiriana del mismo desde el constructivismo sentiente y transcendental. Al finalizar señalaremos una valoración crítica. Atenderemos también, a continuación, la exigencia gödeliana de conceder a la verdad matemática el mismo estatuto que el que poseen las verdades de las ciencias de la naturaleza, a saber, verdades de realidad y verdades empíricas. A pesar de las convergencias de Lakatos y de Zubiri en este punto, sin embargo sus divergencias también serán objeto de una valoración crítica. Porque, ¿entienden lo mismo ambos autores cuando dicen que las verdades matemáticas no son deductivas sino empíricas ?

 

 

1.1 Teorema de Gödel y Lakatos: principio de Conservación de la Falibilidad.

 

Lakatos encuadra el problema de los fundamentos del conocimiento matemático de finales del s. XIX y principios del s. XX en el problema del fundamento del conocimiento en general[5] ; por consiguiente, es a la luz de éste desde donde debe examinarse. Las dos posturas dadas al problema del conocimiento son: 1. El dogmatismo que defiende que es posible el conocimiento y cuya tarea consiste en encontrar un fundamento "infalible" sobre el cual se construya con certeza todas las verdades, y 2. El escepticismo que considera imposible el conocimiento porque no puede evitarse el regreso al infinito. De estas dos posturas, el escepticismo es la que ha ido ganando terreno en las ciencias empíricas, sin embargo, no ha podido penetrar en el área de la matemática, que permanece como baluarte del dogmatismo. Después de cualquier crisis de fundamentos surgen nuevas "escuelas" que restauran la certeza matemática. Las filosofías logicista y formalista de las matemáticas, nos dice Lakatos, constituyen los últimos eslabones "de la larga cadena de filosofías dogmáticas de las matemáticas". (este es el caso de la filosofía objetivista-ideal de la matemática del joven Zubiri, de ahí que le afecte plenamente la crítica de Lakatos a este tipo formalista de filosofía de la matemática). Este es el reto lakatosiano: poner fin al refugio matemático del dogmatismo.

"...Las matemáticas han constituido la orgullosa fortaleza del dogmatismo. Siempre que el dogmatismo matemático de la época entraba en ‘crisis’, una nueva versión suministraba de nuevo genuino rigor y fundamentos últimos, restaurando con ello la imagen autoritaria, infalible e irrefutable de las matemáticas, ...La mayoría de los escépticos se rindieron ante el carácter inexpugnable de este reducto de epistemología dogmática. Ya es hora de lanzarle un reto"[6]

El Teorema de Gödel es precisamente la lanza de Lakatos contra el dogmatismo matemático (como lo será en Zubiri para batirse consigo mismo). Dicho Teorema significa el fracaso del ideal leibniziano de infalibilidad [7] de la matemática, continuado en la doble dirección: logicista (Frege y Russell), y formalista (Hilbert). Pero ¿necesariamente tenemos que adoptar una postura escéptica que se detiene en la duda permanente? Lakatos trata de evitarlo desde una postura mucho más modesta que la certeza: la falibilidad. Esta postura es la aplicación a la matemática de la concepción que Popper defiende en la ciencia. Nos dice:

"El falibilismo crítico de Popper toma en serio el regreso infinito en las pruebas y definiciones, no se hace ilusiones acerca de su "detención", acepta la crítica escéptica de toda inyección de verdad infalible. En su planteamiento no hay fundamentos del conocimiento, ni en la cúspide ni en la base de las teorías, pero puede haber inyecciones de verdad tentativas e inyecciones de significado tentativas en cualquier punto"[8]

Pero, a diferencia de Popper, señala Lakatos:

"Pero albergo sentimientos muy duros contra la teoría lingüística y convencionalista de Popper sobre la matemática y la lógica... Y, en consecuencia, soy falibilista, no sólo en ciencia, sino también en matemáticas y lógica"[9]

Los popperianos (y Lakatos lo es aunque sea con "gafas kuhnianas", como él se autodenomina) contraponen[10] certeza y profundidad. Por tanto, la certeza sólo puede mantenerse al precio de la trivialidad de los contenidos matemáticos. En cambio, la exigencia de profundidad de contenido (sofisticación) nos hace perder pie en la seguridad de la superficie y no tener certeza alguna. Pues bien, el teorema de Gödel significa, según la interpretación que hace Lakatos del mismo, el triunfo en la Matemática de la sofisticación o falibilidad frente a la trivialidad o infalibilidad.

"En realidad, el primer teorema de Gödel constituye un principio de conservación de la sofisticación, o un principio de conservación de la falibilidad" [11]

Aclaramos a continuación a qué programa aplica Lakatos la trivialidad infalible y cómo a partir de los resultados del Teorema de Gödel se propaga la sofisticación y, consecuentemente, la falibilidad matemática. Recordemos que Lakatos, según el nivel en el que se inyecta el valor-de-verdad y el significado de los términos de la teoría, divide a éstas en dos tipos fundamentales: teorías euclídeas y teorías empiristas. Mientras que el Programa Euclídeo pone los fundamentos en el significado y valores-de-verdad de la cúspide, el Programa empirista [12] los pone en la base. De estos dos programas es al Programa Euclídeo al que denomina el Programa de trivialización del conocimiento, en cuanto que las teorías están formadas por axiomas infalibles que constan de términos primitivos perfectamente conocidos, y el tipo de prueba que emplea para demostrar los teoremas garantiza la verdad y la transmite de arriba-abajo.

"Puesto que el Programa Euclídeo implica que todo conocimiento puede deducirse de una conjunción de proposiciones trivialmente verdaderas que constan sólo de términos cargados de significado trivial, lo llamaré el Programa de la Trivialización del Conocimiento" [13] .

Dos tipos de Programas Euclídeos o de Programas de la Trivialización del Conocimiento son: el programa "logicista" y el programa "formalista" de la matemática. Su fin es fundamentar la matemática frente a la crítica escéptica. La pretensión de verdad infalible, de certeza absoluta, la realizan a costa de la trivialización del contenido. Ahora bien, este intento choca con el Teorema de Gödel que pone de manifiesto, según Lakatos, que el regreso al infinito en pruebas y definiciones no puede evitarse. Esto obliga a logicistas y formalistas a admitir la sofisticación y falibilidad del conocimiento.

a) Regreso al infinito y el logicismo de Russell. Lakatos constata el giro dado por Russell desde el dogmatismo, —manifiesto en su afirmación de 1901: "la matemática constituye una reprobación continua de tal escepticismo; pues su edificio de verdades se mantiene firme e inexpugnable contra todos los proyectiles de la duda cínica"[14]—, a su desconcierto posterior que le lleva a abandonar el euclideanismo, y a decir: "la espléndida certeza que yo siempre había esperado encontrar en la matemática se había perdido en un laberinto desconcertante..."[15] . Lakatos señala que Russell no ha sacado todas sus consecuencias del abandono del euclideanismo, a saber,

"El regreso al infinito en las pruebas y definiciones de la matemática no se puede detener con una lógica euclídea. La lógica tal vez explique la matemática, pero no puede probarla. La matemática conduce a una especulación sofisticada que es cualquier cosa menos algo trivialmente verdadero..."[16]

Por consiguiente, según este autor, la pretendida trivialización lógica de las matemáticas degeneró en un sistema sofisticado.

"La teoría lógica de la matemática constituye una especulación estimulante y sofisticada, como cualquiera otra teoría científica. Constituye una teoría empirista, y en consecuencia si no se muestra que es falsa, permanecerá conjetural para siempre"[17]

b) Regreso al infinito y la meta-matemática de Hilbert. Igual que en logicismo, la pretensión de certeza absoluta de la meta-matemática, nos dice Lakatos, choca ante los resultados de Gödel que nos llevan a admitir la sofisticación y la falibilidad de la matemática.

"El segundo teorema de Gödel supuso un golpe decisivo para esta confianza en una meta-matemática euclídea. El regreso al infinito de las pruebas no desaparece en una meta-teoría ‘finitista’ trivial: Las pruebas de consistencia han de poseer la suficiente complejidad como para hacer dubitable la consistencia de la teoría en la que tales pruebas se llevan a cabo, y por tanto están condenadas a ser falibles" [18]

El primer teorema de Gödel es otra manera de mostrar que la meta-matemática no detiene el regreso al infinito en las pruebas. Señala que la formalización que incluye la aritmética "está irreparablemente enferma", porque siempre hallaremos modelos no pretendidos, esencialmente diferentes al pretendido, es decir que en unos se mostrará una fórmula y en otros la contraria, con lo cual siempre habrá verdades aritméticas que son indecidibles en el sistema formal. La verdad y el resultado de una prueba no son equivalentes. Esto supone el final del ‘formalismo’ hilbertiano, que creía haber proporcionado un concepto claro de lo que es una prueba en matemática. Los post-hilbertianos con sus meta-teorías enriquecidas vienen a confirmar la sofisticación y falibilidad.

En conclusión, el Teorema de incompletitud —en manos de Lakatos— es la afirmación del regreso al infinito que implica: falibilidad y sofisticación. ¿En qué punto nos sitúa frente al dogmatismo y al escepticismo? ¿Qué repercusión tiene para la fundamentación de la matemática? Respecto del dogmatismo, es la victoria frente al reto que inicialmente se había planteado Lakatos: acabar con el refugio matemático del dogmatismo, y en concreto de sus dos últimas fortalezas: el logicismo de Russell y el formalismo hilbertiano. Pone fin a la trivialización del conocimiento no sólo en la ciencia, sino también en lógica y matemática. Nunca llegaremos a tener un conocimiento completo ni último de la matemática. Ha costado este triunfo y, sin embargo, ¿no conduce a la derrota escéptica? Responde Lakatos:

"Pero ello no lleva necesariamente al escepticismo matemático: sólo obliga admitir la falibilidad de una especulación audaz"[19]

Su propósito es mostrar que la matemática es conjetural, pero sin que signifique necesariamente abandonar la razón por completo. La matemática no puede seguir sosteniendo su certeza unida a la trivialidad de su contenido, como ha pretendido, por ejemplo, el Positivismo Lógico, sino que tiene que consistir en conjeturas audaces y profundas a costa de su falibilidad.

El regreso al infinito matemático, según el autor, imposibilita la fundamentación de la matemática, (conclusión que no será compartida por Zubiri, como veremos). Lakatos sustituye esta tarea fundamentalista, por el problema del avance del conocimiento. ¿Pero cómo sabemos que avanzamos? Responde: "lo conjeturamos"[20]. La reflexión de Lakatos a partir del Teorema de Gödel nos deja en una situación que despierta los siguientes interrogantes:

"Pero ¿Por qué empeñarse en pruebas ‘últimas’ y autoridades ‘decisivas’? ¿Por qué buscar fundamentos, si se acepta que son subjetivos? ¿Por qué no admitir honestamente la falibilidad matemática, e intentar defender la dignidad del conocimiento falible contra el escepticismo cínico, en lugar de hacernos la ilusión de que podremos reparar, hasta que no se note, el último rasgón del tejido de nuestras intuiciones ‘últimas’? [21]

A la luz de la filosofía de Zubiri, podemos ver que Lakatos tiene una noción "concipiente" de fundamento: pues éste es principio lógico o intuición evidente. Zubiri dará una nueva noción sentiente que permite una salida distinta.

 

 

1.2. Teorema de Gödel y Zubiri

 

1.2.1 Dogmatismo de Zubiri en su filosofía pre-gödeliana de la matemática.

Hasta mediados del S. XIX la matemática se considera como una Correspondencia con el cosmos. La matemática es ciencia de realidad, y la verdad matemática expresión de la esencia del mundo. Y en esta creencia se seguía fielmente la concepción de corte pitagórica-platónica. Sin embargo, la evolución de la matemática, a partir de este momento hasta principios de nuestro siglo, supone la crisis total de la Teoría de la Verdad matemática como Correspondencia con el mundo real. Zubiri menciona en su tesis doctoral, Teoría Fenomenológica del Juicio, algunos de los descubrimientos que llevan al abandono de la Teoría de la Verdad como Correspondencia con el mundo real. La teoría de los conjuntos, que lleva a una concepción del número desde una relación real hasta una especie ideal (clase). La introducción del concepto de infinito actual aleja a la matemática de la experiencia. El descubrimiento de Hamilton de los cuaternios y su definición de los números complejos, abre a la matemática a un plano de creación total. La noción de función se ha distanciado de una imagen de relación empírica. Las geometrías no-euclídeas (del ángulo agudo y del ángulo obtuso) llevan a una ruptura entre espacio geométrico y espacio físico. Estos cambios revolucionarios desde mediados del s XIX en la matemática llevan a la sustitución de la intuición por el método axiomático, y de la noción de verdad a la noción de "validez formal". El criterio de validez matemática es la coherencia interna dentro de un sistema formal y no su correspondencia con la realidad. Hilbert define la verdad matemática como Consistencia. La Teoría de la verdad dominante en la segunda mitad del siglo XIX y principios del s. XX es, pues, la Teoría de la Coherencia o Consistencia de la Verdad, que desplaza a la Teoría de la Correspondencia. Veremos a continuación que esta es la postura adoptada por el joven Zubiri.

Zubiri en su tesis doctoral hemos visto que sostiene una postura objetivista ideal de la matemática. Desde ella propugna una concepción dogmática de la matemática: su conocimiento es absolutamente cierto, sus verdades son apodícticas, y la conservación de este carácter está garantizada por el método a priori. De forma sintética, pero precisa, queda definido este dogmatismo matemático (y de las ciencias que denomina "ideales") en el texto que transcribimos a continuación:

" Las ciencias ideales son perfectamente autónomas; no implican la existencia de su objeto como su esencia específica. Por esto todas estas ciencias son absolutamente ciertas con evidencia apodíctica y se construyen con arreglo al método a priori. Tal es el caso de las Matemáticas, de la lógica, de la Filosofía de los valores, etc"[22].

Zubiri, como diría Lakatos, conserva la Matemática (y las ciencias ideales) como el reducto del dogmatismo. La suerte de las ciencias físicas es muy distinta: parte de evidencias asertóricas y se desarrolla por un procedimiento inductivo. Las leyes físicas son aproximadas y relativas, mientras que, según el joven Zubiri, "una ley matemática tal como el teorema de Pitágoras no admite los predicados citados" [23]

"En efecto: la Matemática se refiere a objetos que no son hechos, al paso que la Física se refiere a puros hechos. Tal es el resultado de nuestra crítica precedente. Ahora bien, un conocimiento que se refiere a objetos ideales tiene origen en una evidencia apodíctica y se desarrolla completamente a priori por rigurosa vía deductiva. La Física, en cambio, adquiere sus primeros juicios por una evidencia puramente asertórica, y se desarrolla por un procedimiento inductivo, ¿Qué quiere decir esto? Esto quiere decir que la ciencia física es puramente aproximada" [24]

Este carácter de certeza absoluta, de evidencia apodíctica, de verdades a priori, de infalibilidad [25], en definitiva dogmático, que el joven Zubiri otorga a la Matemática, es común a las escuelas "logicista" y "formalista" de la matemática. Es la concepción pre-gödeliana dominante. Y Zubiri la hereda de un modo crítico (aunque desde una perspectiva posterior resulte a-crítica) porque, a finales del s. XIX y principios del s. XX, considera que la crítica de las ciencias y en concreto de la Matemática conduce al abandono del método intuitivo y a su sustitución por el método axiomático (Hilbert)[26]. Rechaza totalmente la Teoría de la Verdad de la Correspondencia con la realidad cósmica. Dado que las matemáticas crean arbitrariamente su objeto según libre sistema de postulados[27] ¿cómo se va a corresponder con el cosmos? Así pues, adopta la Teoría de la Verdad de la Coherencia o Consistencia, no sin mezcla de Pragmatismo.

El Teorema de Gödel conmociona esta primera concepción zubiriana de la verdad matemática. El dogmatismo defendido en el área matemática ya no es posible (y por extensión en ninguna otra ciencia que denominaba "ideal"). El criterio de verdad matemática no puede ser estrictamente formal o lógico. Si la consistencia, según el Teorema de Gödel, no puede probarse dentro del propio sistema ¿cómo puede seguir sosteniéndose la Teoría de la Verdad de la Coherencia o Consistencia ? Eso es lo que veremos a continuación.

 

1.2.2 Consistencia formal versus Coherencia real.

Hilbert identifica la verdad matemática con la consistencia de los sistemas formales. Un sistema de axiomas y postulados matemáticos es posible si es consistente o incontradictorio. Lo posible es lo incontradictorio. No tiene su fundamento en la realidad sino que es independiente y anterior a lo real. El primer Zubiri, como hemos señalado, se une a esta concepción. Pero esto es precisamente lo que pone en cuestión el denominado segundo teorema de Gödel. Hay proposiciones matemáticas que son verdaderas y, sin embargo, no pueden demostrarse como teoremas dentro del sistema formal en cuyo lenguaje son formalizadas. Zubiri (siempre atento a los nuevos descubrimientos de la matemática, en un contacto directo con eminentes matemáticos) recoge este resultado y saca todas sus implicaciones filosóficas, exponiéndolas en su obra Sobre la Esencia[28]

"La verdad es que jamás podrá demostrarse positivamente la no contradicción de un verdadero sistema de notas o conceptos objetivos, ni tan siquiera en el dominio de la matemática (teorema de Gödel)"[29]

Estos resultados son decisivos para que Zubiri abandone su anterior Teoría de la Consistencia de la Verdad y su formalismo de la matemática. Ahora bien, si la consistencia no puede ser demostrada en un sistema finito (que sea mínimamente interesante) ¿cuál es entonces el criterio de verdad matemática? El primer Teorema de Gödel, según señalamos, significa la anterioridad de la realidad sobre la verdad matemática. Pone de manifiesto que los postulados afirman el contenido de lo real. Dicho Teorema impone, pues, un nuevo giro en la Teoría de la Verdad, desde un criterio lógico-formal hacia un criterio realista. Según Zubiri, la realidad matemática funda la verdad matemática. Esto le conduce a su Teoría de la Conformidad de la Verdad matemática, que estudiaremos en el siguiente punto Simplemente puntualizamos que no hay que entenderla como la Teoría de la Verdad de la Correspondencia. La vuelta de Zubiri de los "objetos" a la "realidad" no es a una realidad transcendente sino a una realidad transcendental.

Zubiri, teniendo presente que el objeto matemático es una entidad positiva, que primero denomina cosa objetual y posteriormente realidad "en construcción", se pregunta por el alcance del criterio lógico-formal de la no-contradicción. ¿Puede constituir un objeto matemático? Señala que constituye un límite, pero no puede fundar una entidad positiva. No es lo mismo hablar de ‘incontradicción" referido a conceptos objetivos que a realidad física. Y en matemáticas, en la interpretación que hace Zubiri del teorema de incompletitud, no se trata de conceptos objetivos sino de realidad postulada. Y esto es esencial. La unidad real matemática (como de cualquier otra realidad) es solidaridad física. No es simple incontradicción, sino que hay una versión de cada nota al "estar desde sí misma determinada a formar unidad con las demás". Las notas son nota-de las demás. Hay una "vinculación física como momento intrínseco de la realidad física de cada nota". Cada nota existe físicamente en función de todas las demás, respecto de todas y cada una de ellas.

En la matemática, las construcciones sentientes de objetos no son meras posibilidades objetivas sino posibilidades reales (o posibilidades objetuales) del sistema de axiomas o postulados.[30] Esto carecería de sentido si la naturaleza de la matemática fuera lógica: la mera posibilidad lógica sería posibilidad matemática. Sin embargo, insistimos en que el primer Teorema de Gödel muestra que el objeto de la matemática es real, por tanto, su posibilidad no es mera posibilidad lógica[31], sino que es posibilidad real. La posibilidad de los distintos sistemas geométricos no es una posibilidad meramente negativa, sino que ha de ser una posibilidad real positiva. Y de ahí que no basta con la Coherencia formal sino que se trata de la Coherencia real. En el capítulo del Constructivismo sentiente de Zubiri, vimos que la creación matemática ha de tener una unidad coherencial, pero que no es suficiente; para que sea real tiene que proyectarse en la formalidad campal de realidad, entonces es unidad estructural de realidad.

Ciertamente lo contradictorio no podrá realizarse jamás. Pero la cuestión es ¿cuándo es algo contradictorio? El principio de contradicción que afirma que jamás pueden realizarse en la misma cosa y en el mismo aspecto dos notas contradictorias, es verdadero y evidente. Ahora bien, el principio de contradicción con seguridad sólo lo podemos aplicar "en el orden de lo formalmente concebido en cuanto tal" y no en el orden de la realidad. Sólo si tenemos una cosa con las meras notas objetivamente concebidas podemos comprobar si hay o no contradicción entre alguna de ellas. Pero el primer Teorema de Gödel significa que el objeto matemático por ser realidad tiene más notas de las meramente concebidas y deducidas por el sujeto, ¿puede darse entonces la condición para poder seguir aplicando el principio de contradicción a lo que no sea puramente lógico, y en nuestro caso a la matemática?

"Si lo trasladamos del orden de la objetividad al orden de la realidad, es decir, a las cosas en que los conceptos objetivos están realizados según su propia razón formal, la cuestión cambia de aspecto. Porque la condición para que se aplique el principio de contradicción es que se trata de una cosa que no sea sino lo que formalmente contienen las notas objetivamente concebidas. Y aquí empiezan las dificultades. Porque esta condición, ¿es ella misma posible? No lo creo"[32]

Gödel muestra precisamente que el programa de Hilbert al probar que la matemática carece de contradicción es inviable desde un sistema con número finito de axiomas y postulados, no que sea falso. Si la matemática fuera idéntica a la lógica no sería una objeción. Pero no es así; por estar realizados, las definiciones y postulados tienen más propiedades que las notas objetivamente concebidas (Teorema de Gödel). Y no sólo en el sentido de la implicación, que es evidente, sino de todas las propiedades "com-plicadas", "co-puestas", por el mero hecho de haber sido puestas o realizadas. El contenido que expresan los postulados matemáticos al realizarse se abre al "más" en que consiste la realidad y que no se agota en ningún contenido determinado sino que los trasciende a todos.

"No sólo tratándose de cosas reales, sino de objetos, el mero hecho de que se realicen en aquéllas, o de que realicemos nosotros en éstos, varias notas objetivamente concebidas, lleva inexorablemente aparejado consigo el que eo ipso esas cosas u objetos, tengan más propiedades que las que hemos concebido objetivamente"[33]

Y continúa:

Y esto no sólo en el sentido de la implicación. lo cual es obvio: en efecto, si una cosa tiene N propiedades, tiene también todas las que inexorablemente se deducen de ellas, es decir, tiene más propiedades por implicación. No me refiero a esto, sino a otras propiedades que no están implicadas, sino más bien "com-plicadas" con las iniciales, "co-puestas" al ser "puestas" éstas y por el mero hecho de haber sido puestas o realizadas" [34]

Este es un grave problema para la aplicación del principio de no-contradicción a la matemática. Todas estas dificultades inducen a la conclusión que saca Zubiri: el objeto matemático no es un "ser posible" sino una "realidad postulada".

"La realización, sea en el orden físico o en el objetual, es en cuanto tal, raíz de otras propiedades. En tal caso no es que no sea verdadero para esas cosas el principio de contradicción, sino que su aplicación resulta problemática y vidriosa, dado que el sujeto al que se aplica es complejo y la pureza formal del concepto puede sufrir limaduras importantes"[35]

Hay otras dificultades más graves. La aplicación del principio de contradicción requiere acotar la realidad, pero es artificioso puesto que la realidad está toda ella conectada. Un carácter trascendental de la realidad es su comunicación o ex-tensidad. El dato primario es la unidad de la respectividad de la realidad en cuanto tal, esto es, el mundo. Así pues, para la aplicación del principio de "contra-dicción" adecuadamente tendríamos que tener presente "la totalidad de la realidad en su integridad", como sujeto de atribución del logos. Pero este logos no se da en ningún caso en el ser humano.

"De ahí que muchas cosas que pertinazmente han podido parecer contradictorias, no lo sean en realidad y recíprocamente; no porque no sea verdad el principio de contradicción, sino porque la realidad no realiza el supuesto de la "dicción", a saber, contener sujetos desconectados" [36]

No puede identificarse la posibilidad de "entes" matemáticos y su mero concepto incontradictorio, pues, como hemos visto, son insalvables las dificultades de lograr el supuesto en el que se apoya el principio de no-contradicción[37]. La realidad matemática no se apoya en objetos ideales o en un sistema formal consistente. Los conceptos lógicos, frente a toda concepción de corte racionalista, no son fundamentos de las realidades matemáticas en ningún caso. La realidad matemática es posible por un momento esencial físico de la realidad y no por la consistencia de un sistema formal. Se han invertido los términos: no es lo posible fundamento de lo real sino lo real fundamento de lo posible. La realidad matemática es anterior a la lógica matemática. La no-contradicción es un carácter de la realidad dada antes que una necesidad de un concepto. Zubiri quiere disipar el equívoco que sobre este punto se viene cometiendo de aplicar la necesidad lógica como un "a priori" a las afirmaciones que se hace sobre la realidad. Por el contrario, es la realidad la que es incontradictoria y en toda afirmación o realización de una simple aprehensión en ella, nos fuerza a respetar este carácter suyo. El ámbito del principio de contradicción está pues en la afirmación pero en cuanto afirmado y no en el acto de la afirmación[38].

La repercusión del segundo Teorema de Gödel, que acabamos de analizar en Sobre la Esencia, creemos que no sólo afecta a la matemática, sino que también a la propia concepción de la esencia. Y esto es capital. En la Teoría Fenomenológica del Juicio, la matemática y las esencias eran objetos que se hallaban en el mismo "reino platónico de las Ideas", permaneciendo inmutables e infalibles, y fundantes de la realidad. El giro matemático necesariamente conmueve todo lo que se hallaba en ese mismo reino. La esencia no es algo posible, consistente en sí mismo, y que necesita del acto de la existencia para ser realidad; no es anterior a la realidad y fundante de ésta. Por el contrario, el Teorema de Gödel muestra que no puede definirse la consistencia, sino que algo es consistente está en su propia realidad; la esencia es un momento estructural de la cosa real, es la unidad coherencial primaria de notas, que determina la posición de todas las demás notas; y esta realidad es la que funda la posibilidad real. Esta es una de las dimensiones matemáticas en la propia metafísica del autor, que refleja en la práctica la afirmación zubiriana de que una nueva interpretación de la matemática lleva a una nueva filosofía. En este caso, creemos que una nueva interpretación de la realidad matemática lleva a una nueva concepción de la esencia.

El abandono de la Teoría de la Verdad de la Consistencia significa igualmente el abandono de la concepción de Adecuación de la verdad, sostenido por todo tipo de dogmatismo epistemológico. Si un resultado matemático fuera consistente con un sistema de postulados y axiomas, su verdad sería totalmente adecuada al sistema, y por tanto, definitiva. Vemos a continuación cómo el Teorema de Gödel, precisamente porque significa que la realidad es fundamento de la verdad, muestra que la verdad matemática nunca es adecuada a la realidad matemática.

 

1.2.3 Aproximación aspectual de la verdad a la realidad matemática.

Zubiri distingue dos momentos en la verdad del juicio verdadero: 1. la Conformidad, y 2. la Adecuación. Conformidad significa "que aquello que en el juicio se afirma de la cosa real está realizado en ella". Y "Ad-ecuación" significa que lo que se afirma está realizado en la cosa real en forma tal que hay "un recubrimiento total entre la simple aprehensión, cuya realización se da efectivamente en la cosa, y lo que esta cosa es en realidad". La pregunta que nos sale al paso es la siguiente: en la verdad del juicio matemático ¿se da esta distinción entre conformidad y adecuación ?, ¿no son los juicios matemáticos totalmente adecuados? La respuesta de Zubiri en su primera filosofía de la matemática es muy distinta a la que da en su segunda filosofía de la matemática. Y en este giro es esencial la repercusión del Teorema de Gödel. Analizamos una y otra.

Ciertamente esta cuestión ya vimos que la plantea Zubiri en la Teoría Fenomenológica del Juicio . En esta primera concepción el autor considera que "la ciencia física es puramente aproximada" Pero no las leyes matemáticas que eran absolutas y perfectamente adecuadas a su objeto ideal. De ahí su dogmatismo inicial. Para lo que se muestran inadecuadas es para expresar la realidad cósmica, pero es distinto el referirlas a su propio objeto que a la realidad cósmica.

"Toda ley física es aproximada, relativa y simbólica. Aproximada por el carácter aproximativo que tanto cualitativa como cuantitativamente tiene el experimento. Relativa al grado de afinamiento inductivo que se quiera obtener...Finalmente toda ley es simbólica porque la Matemática no es retrato sino símbolo de la realidad, y toda ley física se formula en términos matemáticos"[39]

Añade a continuación:

Y como siempre hay inecuación entre lo absoluto de una función matemática y lo aproximativo de la realidad, resulta que a una ley pueden responder infinitos hechos respecto de los cuales tiene aquélla un puro valor simbólico. Una ley matemática tal como el teorema de Pitágoras no admite los predicados citados" [40]

El teorema de Gödel pone en crisis esta concepción y responde de manera muy distinta a la cuestión: ¿es la verdad adecuada a la realidad matemática? En efecto, según Zubiri, dicho teorema significa que la verdad matemática es conforme, pero no es adecuada a la realidad matemática; es decir, es una aproximación a su realidad "postulada". De este modo no hay diferencia entre las verdades físicas y las verdades de la matemática, en toda verdad dual se da siempre el momento de conformidad, pero no el de adecuación.

"Para la intelección en movimiento, la adecuación será siempre y sólo una meta lejana. De aquí que todo juicio verdadero, toda verdad dual, sea estructuralmente aproximación: es la aproximación gradual a lo real, una aproximación cada uno de cuyos momentos es una conformidad. Toda verdad dual es por esto intrínseca y estructuralmente aproximada dentro de la realidad, aproximada a lo que tendría que ser una verdad adecuada"[41]

Zubiri sale al paso de la objeción de que la matemática enuncia proposiciones exactas de la realidad matemática, de un número, de una figura, etc; y aclara que esto no quiere decir que sean juicios adecuados, sino que su aproximación es de un tipo distinto del de la inexactitud.

"Hay distintos tipos de aproximación... Toda inexactitud es aproximación, pero no toda aproximación es inexactitud. Y esto es esencial para entender otros tipos de juicios, por ejemplo, los juicios matemáticos, la verdad matemática" [42]

La aproximación de inexactitud es la propia de las cosas que son "dadas" en la aprehensión primordial de realidad. Zubiri pone el siguiente ejemplo, si digo "este papel es blanco", hay conformidad pero no hay adecuación, para que ésta se diera habría que precisar es "blanco en tal o cual grado", y así sucesivamente hasta el infinito.[43] Esto evidentemente no ocurre en la matemática. Si digo "dos más dos son cuatro" no tengo que precisar en qué grado de exactitud es así porque es una respuesta rigurosamente exacta. Por tanto, los juicios matemáticos no son aproximaciones en el sentido de gradual inexactitud como en el caso de las realidades "en y por sí mismas". Las realidades matemáticas no son dadas en la aprehensión primordial, sino que son "puestas" en primer lugar por una "definición" de lo que es esa realidad, y en segundo lugar por un "postulado" de su realidad. De estas realidades, construidas sentientemente, la intelección matemática enuncia juicios que son exactos. Pero, a pesar de su exactitud en orden a la conformidad, vuelve a plantearse Zubiri, ¿son adecuados o son meramente aproximados los juicios matemáticos?.

"Y nuestra cuestión está en saber si esas propiedades rigurosamente conformes a la cosa recubren adecuadamente aquello a que se refieren, por ejemplo, a un número o a una figura. Para esto haría falta saber qué ‘es’ esa figura o ese número" [44]

Todo objeto matemático se define y postula no aisladamente, sino en relación con el conjunto entero a que pertenece, "cada cosa [ente matemático] no es sino un ‘aspecto’ de esta totalidad, es una realización aspectual de lo definido y postulado... Sólo de este carácter aspectual recibe su realidad cada "cosa" matemática"[45]. Si el todo sólo fuera el conjunto de las partes postuladas y definidas, éstas serían conocidas en cuanto aspectos de forma adecuada. No es el caso, el Teorema de Gödel hemos visto que pone de manifiesto que lo postulado y definido por ser contenido de realidad, siempre tiene más caracteres que los meramente postulados y definidos. La conclusión que saca Zubiri, es que "entonces, la intelección adecuada de cada cosa en ese todo se deja, en cada paso, fuera de lo definido y postulado, propiedades a las que no alcanza el movimiento intelectivo" [46]. La intelección adecuada sería la que nos diera el conjunto de todas las propiedades, y cada aspecto pudiera ponerse a su luz. Por tanto, hay una distinción entre conformidad y adecuación en matemáticas. Cada conformidad es una inexorable aproximación a una adecuación que tiene más propiedades que lo definido y postulado. De ahí que aunque no tengamos en la matemática aproximación de inexactitud sí que hay aproximación de aspectualidad.

En la concepción logicista y formalista de la matemática no hay esta distinción entre conformidad y adecuación, ello es debido a que el objeto matemático es idéntico al objeto lógico (es la primera concepción de Zubiri). Por ello, el teorema de Gödel pone de relieve estas dos consideraciones: 1. la "realidad" postulada de lo matemático, y 2. el carácter de aproximación aspectual de la verdad matemática. Transcribimos el texto de Zubiri que, con gran lucidez, plasma la potencia filosófica del Teorema de Gödel que en otros autores resulta un barrunto.

"Si la matemática no fuera más que un sistema de teoremas y demostraciones lógicamente encadenadas, la distinción entre conformidad y adecuación no pasaría de ser una sutileza conceptual. Pero la matemática no es eso; es la intelección de realidades matemáticas, dotadas de estructura propia. Por eso es por lo que a mi modo de ver el teorema de Gödel no sólo remite a la "realidad" postulada sino que muestra que respecto de ella toda verdad matemática es una aproximación aspectual, porque aquella realidad tiene una "estructura" propia translógica"[47]

La conclusión que nos arroja el análisis anterior de la verdad matemática, a partir de la interpretación zubiriana del Teorema de Gödel, es que tan aproximada es la verdad matemática como la verdad física a sus respectivas realidades, en un caso postulada y en el otro dada. Tan aplicable es a la física como a la matemática la consideración del autor de que la conformación se da siempre en la verdad del juicio, mientras que la adecuación no. El origen de la distinción entre conformidad y adecuación está en la diferencia entre aprehensión primordial de realidad e intelección en distancia de lo que es en realidad.

"...la simple aprehensión, y por tanto la afirmación de su realización, aun siendo conforme a lo real no es forzosamente adecuada a lo real. No hay ‘ecuación’: tal es el origen de la diferencia que estudiamos. No se debe a la conexión entre el contenido del predicado y el contenido del sujeto sino al carácter de intelección distanciada de lo que la cosa, ya real, es en realidad. Sólo la diferencia entre aprehensión primordial de realidad y intelección en distancia de lo que es en realidad, es el origen de la diferencia entre conformidad y adecuación"[48]

Son dos momentos distintos de la verdad dual pero articulados: cada conformidad apunta hacia la adecuación, como índice de un camino, pero como tal inalcanzable.

"Todos los juicios verdaderos como conformidad, apuntan a una remota adecuación en lejanía. Este punto jamás se logrará alcanzar por un movimiento intelectivo"[49]

Hasta aquí hemos tratado la adecuación como límite en el dinamismo en que consisten los juicios matemáticos. A continuación veremos la dialéctica de la adecuación en la marcha de la razón.

Según Zubiri, la verdad de la razón es verificación. Verificar es probar el esbozo libremente creado como fundamento de la realidad campal en ésta. La verificación no es una cualidad que se tiene o no se tiene, sino que es siempre un ir verificando. El esbozo no se verifica en sí mismo, pero ha de ser suficiente para ir fundamentando lo campal, ya sea en sus consecuencias, en sus concordancias o en sus convergencias. Para que la intelección racional tenga valor científico la verificación tiene que darse también en la línea de la excedencia de lo esbozado respecto del campo que lleva a descubrir nuevas propiedades verificables. En ninguna de las dos líneas la verificación es absoluta, sino que tiene un carácter meramente provisional. Esta provisionalidad es parcial inadecuación. Verificar es ir adecuándose a lo real. Lo esbozado, en cuanto que es más o menos verificado, es más o menos adecuado.

"Claro está, ni la línea de la suficiencia ni la línea de la excedencia son verificaciones absolutas sino una marcha hacia una verificación en lontananza. Cada momento de ella por sí mismo no tiene por tanto valor absoluto sino una verificación provisional. Aquí provisional no significa que va a ser derogado o absorbido, porque ni la derogación ni la absorción son caracteres formales de la marcha verificante... La provisionalidad no consiste sino en parcial inadecuación. La posible derogación o superación o diversificación en la verificación se inscribe formalmente en la adecuación." [50]

La razón humana en cuanto sentiente es una marcha en tanteo. Siente su marcha en la realidad y en ella intelige la realidad en cuanto "realidad-tanteada". Se va tanteando la adecuación de la verificación.

"La razón sentiente es en última instancia razón que se mueve en tanteo, y lo que tantea es formalmente la adecuación de la verificación. La dialéctica de la adecuación es tanteo progresivo de la verificación" [51]

 

1.2.4 Cuestión crítica: regreso al infinito y respectividad de lo real

Lakatos, como hemos visto, considera que el teorema de Gödel significa que el regreso al infinito en matemáticas (como en el resto de las ciencias) no puede detenerse, de ahí que no haya fundamentos infalibles de la matemática. El propio Zubiri experiencia esta exigencia gödeliana que le determina a abandonar el dogmatismo de su primera concepción de la matemática y profesar un cierto escepticismo en la propia intelección matemática. La verdad matemática es conforme, pero no es adecuada a la realidad matemática. La adecuación es inalcanzable, sólo hay aproximación a ella.

Ahora bien, ¿a qué se debe el regreso al infinito en el conocimiento? Dado que ésta es la piedra de toque para decidir el problema del conocimiento, requiere un tratamiento mayor que el de Lakatos. En Zubiri no aparece explícitamente esta cuestión pero sí hay elementos que nos permiten su análisis. Podríamos aventurar que Zubiri formula en Metafísica un teorema equivalente al de Incompletitud de Gödel en la Matemática; lo denominamos: Principio de ex-tensidad de lo real, es el carácter estructural de la realidad en condición de respectividad. Su formulación es: ningún sistema de notas del contenido de una cosa real agota la realidad de la cosa, sino que toda cosa real por su momento de realidad es "más" que el mero contenido de sus notas, y esto porque está abierta a todo lo demás. Toda realidad en cuanto realidad tiene el carácter metafísico de la respectividad. A la unidad de la respectividad de la realidad en cuanto tal la denomina Zubiri mundo. Pues bien, la respectividad de la realidad en cuanto tal es la clave de la remisión infinita de la realidad actualizada. Cada nota remite a otra y "jamás sabremos la amplitud de esta remisión"[52].

"La remisión, en efecto, se funda ante todo en la respectividad constitutiva de lo real en cuanto real, esto es, se funda en que lo real es constitutivamente mundanal"[53]

La regresión infinita del conocimiento se fundamenta, pues, en la respectividad o remisión infinita de la realidad actualizada y no se debe a la mera limitación de nuestro entendimiento. Zubiri y Lakatos tienen por objeto no la trivialidad sino la profundidad y, como ambos señalan, esta cuestión es infinita. Dirá Zubiri que no es lo mismo profundidad y ultimidad, y mientras que la primera es posible, la segunda no. El conocimiento matemático, frente a todo dogmatismo, resulta siempre un problema abierto.

"La profundidad tiene grados; y esta gradación va hasta el infinito. La profundidad tiene hondura insondable. Conocer algo en profundidad no es conocerlo ya en su realidad última. Más aún, la intelección en profundidad es un hecho; pero el acceso a la ultimidad es constitutivamente un problema siempre abierto hasta el infinito"[54]

Pero, insistimos, esta incompletitud del conocimiento se debe a la incompletitud de la realidad. Es la apertura absoluta de la formalidad de realidad la causa de que nuestro conocimiento nunca pueda ser adecuado sino que siempre tendrá carácter provisional. La adecuación es un límite en el infinito. Un conocimiento sería adecuado si tuviéramos presente la totalidad de la realidad, lo cual es imposible por su carácter respectivo. La inagotabilidad de la matemática es un capítulo de la inagotabilidad del conocimiento en general y esto debido a la propia inagotabilidad de la realidad dada en impresión sentiente.

"La realidad es abierta en cuanto realidad, porque su apertura no es sino su constitutiva respectividad. La tarea de la razón es indefinida no sólo en el sentido de que jamás agotará lo que en concreto se propone inteligir, sino que es indefinida ante todo y sobre todo porque lo inteligido mismo, a saber, lo real en cuanto real, es formal y constitutivamente abierto, y por tanto jamás clausurado. En este ámbito abierto, en este mundo, es en el que acontece la búsqueda intelectiva de la razón: es búsqueda en la realidad"[55]

Lakatos y Zubiri nos ofrecen un nuevo modelo de racionalidad, irreductible a cualquier mecanismo, que va tanteando la realidad profunda entre los dos umbrales cognitivos: dogmatismo y escepticismo. La cuestión es si efectivamente en ambos casos se evitan los extremos que anulan el conocimiento mismo. El regreso al infinito es admitido tanto por Lakatos como por Zubiri; su apoyo matemático es el Teorema de Gödel. Por tanto, el dogmatismo matemático queda refutado por Gödel-Lakatos-Zubiri. ¿Y el escepticismo?

Si aceptamos que falible significa conocimiento "penúltimo" y que crítica es acicate de mayor profundidad en la construcción del contenido, es posible compatibilizar el falibilismo que denominamos sentiente y el rechazo del escepticismo, pero si falible es duda y no poseemos seguridad de ningún tipo ¿cómo es posible evitar caer en el escepticismo? Si no hay nada que nos sea dado de modo inmediato para apoyarnos en nuestra marcha o aventura de la razón, ¿cómo podemos ni tan siquiera construir el contenido sin que sea una quimera?, ¿no nos pasaría como a la paloma kantiana que prefiriera el espacio vacío al aire porque éste le ofrece una resistencia, sin percibir la imposibilidad de su vuelo sin ese medio?, ¿es que podríamos ponernos a pensar sin un principio que nos activara a ello, es decir, sin estar ya en el ámbito de la realidad y en el ámbito de la verdad? La falibilidad del conocimiento si nos atenemos exclusivamente al contenido de realidad nos conduce a un escepticismo. ¿No es el falibilismo lakatosiano un falibilismo concipiente?

Creemos que Zubiri fundamenta desde inteligencia sentiente el falibilismo lakatosiano para salvarlo verdaderamente del escepticismo y sin aproximarse ni remotamente al dogmatismo, pues la razón es búsqueda incesante. Pero la firmeza de la marcha intelectiva está dada por el aspecto sentiente de la razón, sentimos que marchamos en la realidad. La formalidad de realidad es un dato infalible que nos es dado sentientemente y por eso nos lanza hacia lo que eso real sea en "la" realidad, y en ello radica toda la provisionalidad del conocimiento. El fundamento de la matemática, pues, según Zubiri, no es inmutable ni último sino que es el momento transcendental de la formalidad de realidad dada en impresión de realidad en inteligencia sentiente. El báculo del falibilismo para no caer en el escepticismo se halla en la línea de la formalidad de realidad. Ahora bien, Lakatos plantea el tema de los fundamentos de la matemática en la línea del contenido, "resbalando" sobre la formalidad, y le hace desembocar en el falibilismo, que en la línea del contenido es incuestionable; sin embargo, la firmeza se halla en la línea de la formalidad: este dato es infalible. Desde la inteligencia sentiente nos hallamos siempre instalados en la realidad, lo problemático sólo será cuál sea el contenido mundanal de una cosa. Zubiri es filósofo falibilista de la matemática en la línea del contenido no en la línea de la formalidad de realidad. En este sentido, denominamos su falibilismo: falibilismo sentiente, frente al falibilismo de Lakatos que es falibilismo concipiente.

"La razón es sentiente. Lo que tiene de sentiente asegura el que sea realidad aquello que intelige, pero el que ésta realidad sea el ámbito de profundidad, abre y constituye la libertad creadora de la razón. Esta libertad concierne al contenido de la realidad profunda"[56]

Las conjeturas no son creación absolutamente libres como supone Lakatos, sino que, según Zubiri, la realidad se impone a la inteligencia en tres modos distintos: como fuerza irrefragable de la formalidad inmediata, como fuerza exigencial de lo real, y como fuerza coercitiva de la realidad. Esta imposición impide la arbitrariedad de nuestra conjetura. Admitir la falibilidad de la matemática contra el escepticismo sólo es posible si fundamentamos la matemática no lógicamente, ni intuitivamente, sino sentientemente. Sentimos que nos movemos en la respectividad de la realidad, pero sin llegar a abarcarla nunca. En la realidad no se trata de evidencias últimas, ni principios lógicos. Este fundamento cumpliría el deseo de la epistemología de Lakatos.

El constructivismo de Zubiri —con sus dos términos congéneres, realidad e inteligencia sentiente, sugeridos en gran parte por el teorema de incompletitud de Gödel— permite fundamentar la verdad matemática y el conocimiento en general frente al escepticismo, pero no de un modo dogmático sino precisamente dando razón del regreso infinito en el conocimiento. Este es su valor histórico.

 

1.3 Exigencia gödeliana: unificación de la verdad matemática con las del resto de las ciencias.

 

A las verdades matemáticas se les ha dotado de un carácter específico frente a las verdades de las ciencias de la naturaleza. La demarcación entre ambas ha consistido en denominar a las primeras "verdades de razón" y "verdades demostrables", y, por el contrario, a las segundas "verdades de hecho" y "verdades de experiencia". Es la clasificación que, por ejemplo, sostiene Hempel (y el neopositivismo). ¿Es esto así? El Teorema de Gödel supone una fuerte conmoción a esta consideración clásica. A partir de éste, se equipara la verdad matemática a la verdad de las ciencias de la naturaleza. Frente a la logificación pre-gödeliana de la verdad matemática nos encontramos con un movimiento inverso de empirificación gödeliana de la verdad matemática, e igualmente de reificación gödeliana de la verdad matemática. Somos conscientes de la gran polémica que suscita estas afirmaciones, y que por tanto decirlas así sin más lleva a graves equívocos. Para evitarlo tendremos que matizar claramente qué se se está entendiendo por experiencia y qué se está entendiendo por realidad, en cada caso. Porque a pesar de las convergencias entre Lakatos, por ejemplo, y Zubiri, está claro que cuando ambos hablan de experiencia matemática no dicen exactamente lo mismo. Y, por último, habrá que ver si la unificación es mera uniformidad o dentro de la unidad hay algún tipo de distinción. La cuestión es de suma actualidad en la filosofía de la matemática, y la solución de Zubiri es original.

 

1.3.1 Verdad matemática: verdad demostrable versus verdad empírica

Así como la logificación de la matemática llevó a la identificación del método matemático con el razonamiento deductivo, en el tema de la verdad va a llevar a la identificación de ésta con la demostrabilidad. Esto comporta que una afirmación matemática es verdadera si es deducible del sistema de postulados del que se parte. De este modo se afirmará que las verdades matemáticas son verdades deductivas frente a las verdades científicas que son verdades empíricas. Es la postura que mantienen la escuela "logicista", la escuela "formalista" y más concretamente el Positivismo lógico. A continuación caracterizaremos brevemente esta postura, siguiendo en nuestro análisis a Hempel, para después ver la crisis gödeliana de la misma.

Hempel en su artículo "Sobre la naturaleza de la verdad matemática" [57] distingue las ciencias empíricas que tienen como criterio de verdad el experimento, de la matemática y ciencias formales por cuyo criterio de verdad se pregunta. Las dificultades que encuentra para considerar que las proposiciones de la matemática son verdades evidentes por sí mismas o autoevidentes son:

1. Muchos teoremas matemáticos no resultan autoevidentes.

2. Algunos resultados de campos como la teoría abstracta de conjuntos y la topología chocan con intuiciones profundamente arraigadas y con el tipo usual de sentimiento de la autoevidencia.

3. La existencia de conjeturas matemáticas como las de Goldbach y Fermat, muestran que no todas las verdades matemáticas pueden ser autoevidentes.

4. La autoevidencia no puede ser una base adecuada para decidir la validez de las verdades matemáticas porque puede variar lo que una persona tiene por evidente respecto a otra.

Hempel, en su análisis crítico, excluye la posibilidad de que las verdades matemáticas sean autoevidentes o intuitivas y llega a la identificación: verdad matemática = demostrabilidad. El autor justifica la sustitución del concepto de verdad por el de demostrabilidad ya que existen construcciones de varios sistemas de geometría que son incompatibles con la euclídea: la geometría hiperbólica descubierta por Lobatchevski y Bolyai, y la geometría elíptica desarrollada por Riemann. Las proposiciones de geometría pura no afirman nada empírico y por esto mismo no pueden ser autoevidentes. Sus teoremas son meramente analíticos y su verdad es a priori, con carácter de certeza por no hacer referencia, como decimos, a ningún contenido fáctico. De este modo, la naturaleza de la matemática pura y la lógica formal es la misma, no establecen ninguna afirmación sobre materias empíricas de hecho. Sin embargo, según Hempel, nos proporcionan un aparato formal para deducir desde unos supuestos teóricos abstractos consecuencias que son concretas y específicas, de tal modo que puedan ser susceptibles de una prueba empírica. La naturaleza de la verdad matemática la establece el autor según el método que considera propio de la matemática: la demostración. Y en la línea que denominamos "logificación de la matemática", quedan identificados método y lógica. Y correlativamente verdad y demostrabilidad.

Hempel está convencido de la certeza y necesidad de los resultados de la matemática. A diferencia de la provisionalidad de las teorías de la ciencia empírica, las verdades matemáticas son definitivas, pues ningún descubrimiento empírico puede afectarles. Por tanto, la base de la necesidad matemática está en el carácter puramente deductivo de la demostración matemática. La deducción lógica es un mero análisis conceptual. Siguiendo la terminología kantiana, puede decirse que es una operación de análisis y no de síntesis; explicita lo que ya está contenido en un conjunto de premisas dado, pero ninguna conclusión añade nada al contenido en las suposiciones iniciales. Hempel sostiene que un teorema matemático es cierto relativamente al conjunto de postulados a partir de los cuales se deriva, el teorema es verdadero si son verdaderos los postulados. Al carecer de contenido empírico, una verdad matemática es irrefutable. Así todo teorema, por ejemplo, de la geometría, que es el primer modelo histórico de ciencia deductiva, resulta analítico en el sentido lógico, en función de los postulados, y, de este modo, su verdad es a priori. Esto significa que su verdad no depende de los datos empíricos sino que se obtienen a partir de la lógica formal.

¿Es esto así? ¿Es idéntica la verdad matemática a la demostración lógica? Desde el Teorema de Gödel está claro que no. Las palabras de W. V. Quine condensan el significado del Teorema de Gödel como una "sacudida" a la concepción clásica de verdad matemática. Dice:

"El descubrimiento de Gödel constituyó una sacudida a la concepción clásica. Se suponía que la misma naturaleza de la verdad matemática era su demostrabilidad. Pero no es así"[58]

Comprobar que una proposición sea verdadera es distinto a comprobar que sea demostrable. La verdad de una proposición no nos asegura su demostrabilidad. Efectivamente, según ya hemos expuesto, esto se puede concluir del Teorema de Gödel, según el cual hay verdades que no son "deducibles" del sistema de postulados y definiciones. De modo independiente Tarski llegó también en 1929 a la imposibilidad de reducir el concepto de verdad al de demostrabilidad en un sistema deductivo apropiado. Estos resultados matemáticos de Gödel y Tarski apoyan la superación de posturas como la de Hempel y el positivismo lógico. Lo vamos a ver en Lakatos y posteriormente en Zubiri.

El Teorema de Gödel supone[59] para Lakatos el renacimiento del empirismo en la reciente filosofía de la matemática. Lakatos pone de manifiesto que no es un hecho aislado sino que se da en numerosos[60] filósofos de la matemática. De este modo queda invalidada (Zubiri se suma a ello) la siguiente demarcación logicista[61] de las ciencias sostenida, como hemos visto, por Hempel y el positivismo lógico:

 

Demarcación logicista
Ciencias Naturales	Matemáticas
a posteriori	a priori
empíricas	demostrativas
falibles	infalibles

 

 

El reto lakatosiano es mostrar que la deducción no es el patrón de la lógica del descubrimiento matemático del mismo modo como Popper mostró que la inducción no es la lógica del descubrimiento científico[62]. Lakatos reconoce la paternidad popperiana de la metodología empírica; y trata de mostrar, por primera vez, "...hasta qué punto el sistema conceptual popperiano de la lógica del descubrimiento en las ciencias empíricas es aplicable a la lógica del descubrimiento en las ciencias cuasi-empíricas y a la matemática en particular"[63]. Una deducción no aumenta el contenido y, por tanto, es puramente analítica y estéril. Lakatos afirma: "el estilo deductivista, esconde la lucha y oculta la aventura". La sofisticación y la falibilidad destruyen "el mito de la deducción infalible". Esquemáticamente veamos, el giro del ideal euclídeo-demostrativo al ideal cuasi-empírico.

 

Ideal euclídeo	versus	Ideal cuasi-empírico
Busca verdades auto-evidentes,		Busca "hipótesis imaginativas y audaces con una gran potencia explicativa y heurística". Es siempre conjetural.
Lógica infalibilista del descubrimiento.		Lógica falibilista del descubrimiento.
El método es la deducción—prueba demostrativa—de teoremas.		El patrón dialéctico es: conjeturas, pruebas y refutaciones.
La lógica es organon de prueba. El resultado es el desarrollo continuo y acumulativo de verdades eternas		La lógica es organon de crítica. Lucha de teorías competitivas. Revolución permanente y Proliferación de teorías

 

 

Constatamos que este renacimiento post-gödeliano del empirismo en la verdad matemática, del que habla Lakatos, se da también en Zubiri. Pero ya advertimos que esta expresión es peligrosa. Veamos de qué modo esto es así. Zubiri, tras abandonar el logicismo de la verdad de su primera filosofía de la matemática, afirma enérgicamente desde su concepción constructivo-sentiente de la verdad que ésta no se reduce a verdad lógica. Las verdades matemáticas no son meramente verdades deductivas, sino que son verdades idénticas a las de las ciencias naturales: de experiencia. Toda verdad, del tipo que sea, según Zubiri, es verdad de experiencia. Pero ¿Cómo hay que entender el término "experiencia" en el autor? No se trata de experiencia "sensorial". La experiencia matemática, ya lo vimos, consiste en la probación física de realidad postulada. No es algo meramente dado, sino que es un logro de profundización dentro de la realidad dada y sin salirnos de ella. No es un experimento extramental. Sólo desde esta concepción zubiriana de experiencia, es inadmisible la distinción verdades empíricas y verdades demostrables. Las verdades matemáticas son "probación física" de realidad de igual modo que las verdades de las ciencias naturales. En este caso las realidades son dadas y en el primero son postuladas, pero esta distinción no afecta al sentido de experiencia de realidad. Al ser el objeto matemático real y no conceptivo, necesariamente nuestra forma de conocerlo es experiencial y no demostrativa. Precisamente porque el método constructivo-sentiente es vía en la realidad postulada de la matemática, podemos obtener verdad matemática. La verdad matemática es verdad del contenido de la realidad matemática y no está carente del mismo como dice Hempel. Claro que realidad no es realidad "allende" la aprehensión primordial.

Zubiri tiene un concepto de realidad y experiencia distinto del empirismo lógico. Y es fundamental insistir en ello. Como el contenido de la realidad matemática es evidente que no es aprehendido primordialmente, esta constatación induce a la postura que niega el carácter de realidad al objeto matemático, y, consecuentemente, si no es ciencia de realidad tampoco es ciencia de experiencia, y, una última deducción, si no es ciencia de experiencia no puede hablarse de verdad sino meramente de validez. Desde un punto de vista más actual que el del empirismo lógico, el matemático y filósofo de la matemática MacLane, fundador de la escuela denominada por él mismo: "funcionalismo formal", llega a estas conclusiones, contrarias a la empirificación de la verdad matemática.

El Teorema de Gödel ha abierto un "palpitante" debate sobre si la verdad matemática es demostrativa o empírica. Para hacer de Zubiri un interlocutor válido en esta discusión actual hay que esclarecer los términos de realidad y de experiencia tal y como son creados por él, sólo así evitaremos los malentendidos a que puede dar lugar su concepción. Por ejemplo, la postura de Camino Cañón en este punto ¿cómo afecta a la concepción de Zubiri? Consideremos, en primer lugar, sus palabras que aluden de forma concreta en el siguiente texto a Wilder.

"Tampoco nos parece aceptable el situar la Matemática al nivel de las creencias empíricas y su verdad, en continuidad con la de aquellas.

Con Shanker pensamos que "hay una diferencia categorial entre la verdad de las proposiciones matemáticas y la de las proposiciones empíricas’. Aunque nuestro modo de defender este punto de vista no está construido con la argumentación de este autor wittgensteiniano..." [64]

La nivelación que Wilder hace de la Matemática con las ciencias naturales, que le conduce a una total relativización del conocimiento matemático y a una concepción pragmatista de la verdad, rechazado por la autora, ¿es del mismo tipo de la de Zubiri? ¿Y tiene las mismas consecuencias?. Al final del último capítulo de su libro Matemática: descubrimiento y creación, Camino. Cañón hace una conclusión contraria a la que nos lleva el estudio zubiriano:

"Terminamos esta reflexión en la que hemos pretendido ofrecer una concepción de la matemática que no renuncia a la relevancia de la historia en su construcción, sin aceptar por ello tratarla como una ciencia empírica. Es un producto cultural de la racionalidad humana que goza de una especificidad que las modas pueden ocultar, pero nunca destruir" [65]

¿Qué está entendiendo la propia autora por experiencia que le lleva a negarla como vía de encuentro de verdad matemática? ¿No es el mismo concepto que tiene Wilder y por ello lo rechaza? ¿Es lo mismo experiencia en Wilder que en Zubiri? Creemos que no. Zubiri rechaza también la identificación de la matemática con la experimentación física. Pero ello no le lleva a la negación del carácter empírico de la matemática, sino que su ruta es otra: negar la concepción que se está suponiendo sin discusión de lo que es experiencia, y alumbrar otra muy distinta, desde la cual puede afirmarse el carácter empírico de la matemática. Zubiri en esta discusión comenzaría preguntándose ¿quién ha dicho que "experiencia" es lo que entienden Wilder, W.Q. Quine, y en el fondo que sea el concepto de "experiencia" que tiene Mill? Zubiri, como Camino Cañón, rechaza que esta noción de experiencia sea adecuada a la matemática, ahora bien, como hemos dicho, no por ello niega el carácter empírico a la matemática, sino que modifica la noción misma de experiencia, enriqueciéndola de tal modo que resulta adecuada no sólo a la matemática sino a todo tipo de verdad racional. Esta nueva noción de experiencia sólo es posible desde una nueva concepción de inteligencia. No se trata de inteligencia concipiente sino de inteligencia sentiente. Zubiri sustituye la noción concipiente de experiencia por una concepción sentiente de la misma. De ahí la importancia de la noología de Zubiri como presupuesto de su original filosofía de la matemática. Este punto de partida le permite una radicalidad en su planteamiento que no es el usual.

Además en este debate actual, hay que hacerse otra pregunta: ¿De qué tipo de nivelación se trata entre matemáticas y ciencias naturales? ¿Hay una total uniformidad entre las verdades matemáticas y las verdades de las ciencias naturales? El mismo Lakatos llama a las verdades matemáticas: cuasi-empíricas. Ese "cuasi" es indicador de que no hay total uniformidad. Según Zubiri esta uniformidad tampoco se da. Aunque las verdades matemáticas son verdades empíricas, no son exactamente iguales a las verdades de las ciencias naturales. En efecto, el autor tiene un concepto tan rico de experiencia que le permite distinguir cuatro tipos distintos de experiencia: experimento, compenetración, comprobación, conformación. Pues bien, mientras que las verdades matemáticas son verdades de com-probación, las verdades de las ciencias naturales son verdades de experimentación. La distinción entre los modos de experiencia: experimento y comprobación, ha sido totalmente ignorada en la filosofía de la matemática, con consecuencias graves como hemos visto. La pobreza del término experiencia entendido sólo como experimento es lo que ha llevado a negar a la matemática su carácter empírico. O, en menor medida, a darle un carácter empírico que desvirtúa la naturaleza de la matemática como ocurre con la concepción del empirismo "sensualista". Pero ¿cómo vamos a experimentar en la realidad postulada de la matemática? Experimento, consiste, según el autor, en forzar a la realidad campal (sea inanimada o también seres vivos incluido el ser humano) a mostrar al experienciador su índole profunda. La realidad matemática ya vimos que no es en razón de su contenido una parte de la realidad campal, y por tanto no es experimentable. El experimento es una provocación de la realidad desde un esbozo de posibilidades, como modo de intelección; hay una intervención manipulante del experienciador. En la matemática, según Zubiri, no se trata de experimentar sino de comprobar. La prueba matemática no es un "cuasi-experimento" es otra cosa. En la comprobación, ya lo explicamos, se prueba la presencia de la realidad "en" la verdad deducida. Lo real aprehendido es lo que verdadea "con" la afirmación. Es com-probación de la realidad en su verdad.

Como la mente humana, en general, tiende en exceso a asimilar los esquemas nuevos a los esquemas anteriores, podríamos decir que esto es un mero cambio de lenguaje, y, que en el fondo, la distinción entre verdades comprobables y verdades experimentales, es lo que clásicamente se establece entre verdades demostrables y verdades empíricas. Creemos que no es un mero cambio lingüístico sino que responde a un verdadero cambio conceptual, esto es, paradigmático. El estatuto de la verdad matemática es muy distinto al lógico. Esquemáticamente:

 

Empirificación de la verdad matemática
Verdades de razón	versus	Verdades de experiencia
La verdad de razón es a priori		No es verdad a priori
Se identifica con demostrabilidad		Se identifica con experienciación
Se funda en conceptos de nuestra		Se funda en realidad dada

 

 

En conclusión, la nueva concepción de la verdad matemática que arroja el teorema de Gödel, supone para Lakatos y Zubiri la inviabilidad de la logificación de la verdad matemática. Y es un común denominador en los filósofos de nuestro tiempo. Sin embargo, Lakatos (lo mismo que Quine, y en general) incurriría, si se nos permite, en una "empirificación" de la verdad matemática desde la logificación de la intelección o inteligencia concipiente, mientras que Zubiri se une a esta "empirificación" de la verdad matemática pero desde la empirificación de la intelección, esto es, desde la inteligencia sentiente .

Esta postura de Zubiri resulta, pues, que está "a la moda" (como denomina Camino Cañón la corriente de empirificación de la matemática), pero sui generis. Digamos que está "a la altura de los tiempos". Es lo que denominamos en el encabezamiento de este punto: exigencia gödeliana de la unificación (no uniformación) de la verdad matemática con el resto.

 

1.3.2 Disolución de la distinción: verdades de razón (necesarias) y verdades de hecho (contingentes)

La unificación de la que hemos tratado en el punto anterior entre verdades matemáticas y verdades de las ciencias naturales, ¿significa que las verdades matemáticas no son verdades necesarias? [66], ¿son, por tanto, verdades contingentes? Esto es lo que parecen afirmar los autores que señalan que las verdades matemáticas son verdades empíricas. Ahora bien, antes de responder esta cuestión hay que hacerse la siguiente pregunta: ¿Es correcta la distinción leibniziana entre verdades de razón y verdades de hecho, y entre verdades necesarias y verdades contingentes? Pensamos que igual que en el debate actual sobre la cuestión: ¿son las verdades matemáticas demostrables o empíricas? no se ha discutido el significado de experiencia, y si hay verdades que sean meramente demostrables; así en la discusión sobre cuál es el carácter de las verdades matemática ¿necesario o contingente?, ¿de razón o de hecho?, no se ha puesto en cuestión la validez misma de esta distinción. ¿No es una distinción concipiente? ¿Pero es que hay verdades meramente de razón? ¿Hay verdades absolutamente necesarias? Nuestro filósofo vuelve a tocar un tema de suma actualidad e interés en la filosofía de la matemática.

Es clásica, desde Leibniz, la distinción entre verdades de hecho y verdades de razón, y la consecuente distinción entre verdades contingentes y verdades necesarias. Pero ¿son las verdades matemáticas verdades de razón? Actualmente se defiende en filosofía de la matemática tanto una cosa como otra. Por ejemplo, Quine rechaza que exista esta distinción entre verdades contingentes y verdades necesarias. Para este autor la experiencia puede afectar a los resultados matemáticos considerados ciertos, por tanto no son verdades necesarias. Esta postura, a su vez, es criticada por Kneale:

"Quine va demasiado lejos cuando trata de abolir la distinción entre verdades contingentes y verdades necesarias. Por una parte, los enunciados históricos y geográficos no podrán por menos de seguir siendo siempre contingentes, ya que no tendría objeto recurrir a la legislación lingüística con el fin de excluir las posibles alternativas a los mismos; mientras, por otra parte, enunciados tales como "Nada es completamente rojo y verde al mismo tiempo" habrán de ser de entrada necesariamente verdaderos, ya que se hallan garantizados por las reglas que de entrada admitimos y seguimos al tratar de distinguir unos de otros los diversos colores". [67]

La filosofía matemática de Zubiri ¿arroja alguna luz sobre esta cuestión? ¿Es admisible la distinción? Nuestro autor considera que la división entre verdades necesarias y verdades contingentes, o entre verdades de razón y verdades de hecho, es "conceptiva" y como tal inadecuada. Él expone su concepción realista de la verdad matemática al hilo precisamente de su crítica a la postura de Leibniz, uno de los precursores de la escuela logicista de la matemática.

¿En qué se basa la división de Leibniz? Las verdades de razón son verdades necesarias, es decir es imposible pensar otra cosa; se fundan en el principio de contradicción. Y las verdades de hecho son verdades contingentes, es decir no hay contradicción en pensar que pueden ser de otra manera. El autor compara la distinción entre verdades necesarias y verdades de hecho con la de de los números racionales e irracionales. Las verdades necesarias se reducen en último término a verdades idénticas captadas inmediatamente por la mente, pero en las verdades de hecho, como en los números irracionales, se prosigue continuamente hasta el infinito sin hallar una razón última de su verdad. De ahí que la certeza y razón perfecta de las verdades contingentes sólo es conocida a Dios. Son verdades de razón sólo para una mente divina no para la humana. Esta concepción racionalista de Leibniz es insostenible para Zubiri. Dice:

"Para Leibniz la verdad de razón es formal y constitutivamente necesaria: no puede ser de otra manera, es imposible pensar lo contrario. Por esto, la verdad de razón sería verdad eterna. En cambio, la verdad de hecho es verdad sobre algo que puede ser de otra manera; es posible lo contrario de ella. Por eso es verdad contingente.

Pero esta concepción es, a mi modo de ver, insostenible"[68]

Dejando aparte, dice el autor, que la mente humana es finita y como tal sus verdades serán siempre limitadas y que sólo una mente eterna puede aprehender una verdad eterna, lo verdaderamente grave de este error está en su falta de radicalidad, porque la distinción fundamental no está en verdades de hecho y verdades de razón. No se trata de verdades de ser objetivo sino que se trata de verdades de realidad. La verdad no es cuestión de identidad mediata o inmediata de conceptos. Toda verdad, desde la inteligencia sentiente, es primariamente verdad de realidad y no de conceptos objetivos. Y como toda realidad es dada, entonces, nos dice Zubiri, la distinción entre verdad de razón y verdad de hecho, y entre verdad necesaria y verdad contingente, es falsa. Esto hay que entenderlo en el sentido de que la base de toda verdad es el ámbito transcendental de realidad. En éste se construye toda libre creación de la inteligencia. Desde el punto de vista del transcendentalismo matemático, las verdades matemáticas no son verdades de razón, sino verdades de realidad.

"Para Leibniz la verdad es siempre cuestión de ser objetivo, esto es, de conceptos objetivos, y su ser está inteligido en esa forma de afirmación que es la identidad. La verdad es siempre identidad mediata o inmediata de conceptos. Pues bien, esto no es exacto. La verdad no es cuestión de conceptos objetivos sino de realidad. Y la realidad es siempre algo primaria y radicalmente dado, algo meramente actualizado en la intelección. De aquí que la distinción de Leibniz entre verdades de hecho y verdades de razón, entre verdades necesarias y verdades contingentes, sea falsa" [69]

Según Zubiri, la verdad siempre es verdad de realidad. La distinción de tipos de verdades sólo es admisible dentro de la misma línea de realidad. Hay verdades de realidad campal y verdades de realidad mundanal. La primera concierne a las cosas reales en el campo de la realidad, y la segunda al mundo mismo de lo real.

"la diferencia radical no es una diferencia entre hecho y necesidad, sino la diferencia entre realidad campal y realidad mundanal, que es cosa distinta" [70]

Desde la inteligencia sentiente, pues, hay que decir que la cuestión de si la verdad matemática es necesaria o contingente, está mal planteada porque supone una dualidad que no existe. Zubiri es tajante en negarla:

"De aquí que la distinción de Leibniz entre verdades de hecho y verdades de razón, entre verdades necesarias y verdades contingentes, sea falsa"[71]

Basándose en esta distinción, la matemática y la lógica se han considerado verdades necesarias, en cuanto verdades de razón que nada tenían que ver con la experiencia y por tanto irrefutables por ésta. Mientras que las ciencias empíricas se consideraban verdades contingentes, en cuanto que son verdades de hecho y por tanto dependientes de la experiencia. Este criterio lo han defendido racionalistas como Leibniz, y empiristas como Hume. Este es escéptico en cuanto a todo el saber excepto la matemática y la lógica que serían meras relaciones de ideas conformes con el principio de identidad.

"Todos los objetos cuya investigación se propone la razón humana, se dividen naturalmente en dos clases; la primera comprende las relaciones de ideas, la segunda, las cosas de hecho. A la primera pertenecen todas las proposiciones de geometría, de álgebra y de aritmética; en una palabra, todas las que son o intuitivamente o demostrativamente ciertas...

Las proposiciones de este género se descubren por simples operaciones del pensamiento, y no dependen en nada de las cosas que existen en el universo. Aunque no hubiese ni círculo, ni triángulo en la naturaleza, los teoremas demostrados por Euclides conservarían igualmente su evidencia y su verdad siempre[72].

Para Zubiri, la realidad no es sinónimo de contingente, es mera formalidad de lo aprehendido. Y lo sentido por el hecho de ser sentido tampoco es sinónimo de contingente. Según el constructivismo transcendental, las verdades matemáticas (lo mismo las verdades lógicas) no se fundan sólo en conceptos de nuestra mente sino que se fundan en realidad dada. Lo primario es la necesidad física y no la necesidad lógica. La necesidad física es la que nos lleva a la necesidad lógica y no al revés. Las verdades matemáticas, no son absolutamente necesarias sino que su necesidad depende de la realidad construida por postulados. Si cambiamos la realidad postulada cambian las verdades matemáticas. La suposición de que las verdades matemáticas son independientes de la realidad es lo que ha llevado a pensar que son eternas. Pero, según el constructivismo transcendental, no son verdades independientes de la realidad postulada, y no son, por tanto, verdades eternas.

"...las presuntas verdades de razón, ¿son verdades eternas en el sentido de Leibniz? Ciertamente no"[73]

"...se fundan intrínsecamente en realidad ‘dada’. Las verdades matemáticas son ciertamente necesarias, pero su necesidad pende de postulados, por tanto de realidad dada en y por postulados. En última instancia, las verdades matemáticas están ancladas en algo dado. Y por esto, podrían ser perfectamente de otra manera. Los postulados están, en efecto, libremente elegidos. Me bastaría con cambiar los postulados y la verdad matemática sería otra"[74]

La concepción de la verdad matemática hay que entenderla a la luz del constructivismo y transcendentalismo de la matemática. Estos dos aspectos no son contradictorios sino que se concilian en la construcción matemática. Por la inteligencia sentiente estamos en "la" realidad como ámbito transcendental y en él se proyectan los contenidos creados por postulados y axiomas. Esta realidad dada (transcendentalismo) "en y por postulados" (constructivismo) es la que "verdadea" en la intelección. Si cambia el contenido libremente construido del ámbito transcendental de realidad, entonces cambian las verdades matemáticas. Unos postulados nuevos originan un nuevo contenido de realidad transcendental, y, por consiguiente, una nueva verdad matemática. De ahí que las verdades matemáticas no sean necesarias en sentido absoluto, sino meramente relativo a "la realidad dada en y por postulados". El ámbito transcendental es campo de funcionalidad que se nos impone coercitivamente de tal modo que no nos salgamos de la realidad en la libre construcción de su contenido. El esbozo, como vimos, siempre es libremente construido y por eso no es de necesidad absoluta. Más adelante trataremos la cuestión de la historicidad de la verdad matemática, en cuanto realización de un sistema de postulados y axiomas.

Si la verdad matemática no es eterna, tampoco la lógica. El principio de contradicción antes que un principio lógico, nos dice Zubiri, es un principio de la realidad. Es la realidad inteligida que no puede ser de otra manera la que nos impide pensar lo contrario de ella. Aquí hallamos la respuesta zubiriana al texto inicial de Kneale[75]. La verdad de las afirmaciones no depende de unas reglas admitidas o de unos principios lógicos, en este caso del principio de contradicción. El ejemplo que pone Kneale, "Nada es completamente rojo y verde al mismo tiempo" depende de los caracteres de la realidad dada, es la imposibilidad real de esto la que nos lleva a la imposibilidad lógica y no al contrario. Dice Zubiri:

"Las verdades lógicas no son necesidades de conceptos sino caracteres de realidad dada. Si no se puede pensar lo contrario de ellos, no es porque su verdad sea eterna, sino porque la realidad inteligida misma como realidad, esto es, la afirmación en cuanto afirmada, es la que no puede ser de otra manera"[76]

Zubiri ante el equívoco al que se presta el término verdad de razón, puesto que no se trata de verdad de razón propiamente si por tal entendemos verdad de conceptos, sino de verdad de realidad, mundanal y cósmica de lo real campal, prefiere sustituir el término de "verdad de razón" por el de "verdad racional".

"...verdad racional no consiste en ser verdad de razón sino en ser verdad mundanal y cósmica de lo real campal"[77]

Una última aclaración sobre la distinción entre necesario y contingente, ¿niega Zubiri que exista la distinción entre necesario y contingente? Si hablamos de verdades, en efecto, no existe esta distinción entre verdades necesarias y verdades contingentes; sin embargo si hablamos de realidades, por el contrario, se da la distinción entre realidades necesarias y realidades contingentes. Es un problema de metafísica. Por tanto, únicamente puede hablarse de verdades de realidad necesaria o verdades de realidad contingente. La realidad en un caso será contingente y en otro caso podrá ser necesaria, pero no son dos caracteres en ningún modo de la verdad. Las verdades de las matemáticas, en cuanto verdades, son verdades de realidad del mismo modo como lo son las verdades de las ciencias naturales.

"Por tanto, no existen dos tipos de verdad, verdad de hecho y verdad de razón. Toda verdad es siempre y sólo ‘verdad de realidad’. Lo que sucede es que esta realidad es o bien realidad sentida como campal, o bien realidad mundanal y cósmica. Pero en ambos casos se trata de una misma e idéntica realidad en cuanto realidad. La realidad campal nos impele desde sí misma, en su modo de ‘hacia’, a lo mundanal; y lo mundanal está inteligido en lo real campal pero como encuentro y cumplimiento de un esbozo. Y este encuentro es la verdad racional’.[78]

Este texto es difícil de aplicar a la matemática; a nuestro modo de ver, en la filosofía de la matemática de Zubiri, no está claro cómo hay que entender las verdades campales y las verdades racionales en el dominio de la matemática. Si tomamos "lo real campal" como lo dado inmediatamente tanto en su contenido como en su formalidad de realidad, no habría ningún objeto matemático meramente campal, porque el contenido es construido en todos los casos. Luego, sólo podríamos hablar de los objetos matemáticos como realidades mundanales (pensadas transcendentalmente); y las verdades matemáticas serían exclusivamente verdades racionales, no campales. Sin embargo, Zubiri habla, respecto de la matemática, tanto de verdades campales como de verdades mundanales. Esta dificultad puede resolverse si tomamos la noción de "objetos en el campo" aplicado a la matemática no como objetos con un contenido dado inmediatamente, sino con un contenido dado "en y por postulados". La creación y descubrimiento (ya analizaremos más adelante la relación de estos términos) de nuevos objetos matemáticos enriquecen el campo de la matemática. La intelección campal consiste en inteligir un objeto matemático en función de otros objetos dados ‘en y por postulación"; por ejemplo, si intelijo "7+5" entre otros números y afirmo que es "13" y no cualquier otro número, se trata de un tipo de intelección campal o del logos. En la intelección campal o logos no hay propiamente búsqueda (ni encuentro), no hay esbozo (ni cumplimiento), sino un mero movimiento "entre" otras realidades postuladas. Por el contrario, en la intelección racional o mundanal hay una marcha que consiste en búsqueda y esbozo de un libre sistema de postulados y axiomas. Según la interpretación expuesta, el tipo de dinamismo de la inteligencia (movimiento o marcha) es lo que decide el tipo de verdad matemática, si es campal o si es mundanal

Otro criterio también válido en la matemática es la forma de realizarse "lo irreal" en el objeto matemático dado "en y por postulación", si es como nota es intelección campal y si es como fundamento es intelección racional. Pues bien, en estos dos sentidos puede aplicarse las nociones de campo y mundo a la matemática. La dificultad surge cuando queremos aplicarla en el sentido de las cosas sensibles, y exigimos a todas las cosas campales que tengan un contenido sensible. Esto nunca se da en la matemática en sentido primario, sí por "sensibilización" del contenido (según vimos en el constructivismo sentiente). Lo mundanal matemático está inteligido en lo real campal, pero no en unos contenidos sentidos concretos (un color, un sonido...), sino en la funcionalidad del campo (que nos es dada inmediatamente por las cosas "en y por sí mismas"), y es inteligido en el campo de funcionalidad de la realidad como encuentro y cumplimiento de un esbozo.

Pensamos que la dificultad planteada en la matemática, a propósito de los términos, "intelección campal" e "intelección mundanal", también se resuelve, en parte, si los sustituimos por "razón campal" y "razón mundanal". Puede resultar contradictorio decir "razón campal", sin embargo, Zubiri utiliza este término,

"Ahora bien, sentir algo como real es justo intelección sentiente. La intelección de la que la razón campal es modo, es la intelección sentiente. Sentiente no significa (ya lo vimos), que su objeto propio, primario y adecuado es sensible."[79]

 

2. Teoría de la Conformidad de la verdad matemática con lo real

 

En el constructivismo transcendental de la matemática, señalamos que la interpretación zubiriana del primer Teorema de Gödel consiste en la anterioridad de la realidad sobre la verdad. Y en el punto anterior hemos visto que el segundo Teorema de Gödel lleva a Zubiri al abandono de la Teoría de la Verdad como Consistencia, puesto que no es posible su probación en un sistema formal. Supone también un giro desde su concepción de la verdad matemática como verdad de razón, a priori, demostrativa, necesaria... a una concepción de la verdad matemática como verdad de realidad y de experiencia, dependiente de la postulación de realidad. Todo ello induce a la concepción de que la realidad funda la verdad matemática. Ya quedó esta cuestión más o menos adelantada en la comparación de la filosofía de la matemática de Zubiri y la de Lakatos, a propósito del problema sobre el fundamento de la verdad matemática.

A continuación veremos de qué modo la realidad puede fundar la verdad matemática, la aportación zubiriana a la concepción de la verdad matemática consistente en la teoría de la Verdad como Conformidad de la verdad matemática con la realidad matemática, y cómo hay que entenderla para evitar equívocos. Tratamos la cuestión en tres apartados:

1. La verdad real como fundamento de la verdad de Conformidad.

Toda verdad de conformidad envuelve la verdad real. Ahora bien, ¿Cuál es la verdad real de los objetos matemáticos? Esta cuestión es capital.

2. La verdad de Conformidad en la intelección matemática campal.

Ya apuntamos que el Teorema de Gödel nos lleva a la distinción entre conformidad y adecuación en la verdad campal matemática. Teniendo esta distinción en cuenta, podremos referirnos a los caracteres de la conformidad del logos matemático: evidencia, rigor, exactitud y certeza, sin que creamos que esto significa una total adecuación del juicio con la realidad matemática. Hay conformidad en los juicios matemáticos, adecuación no. Por otra parte dilucidaremos si estos caracteres de los juicios matemáticos (que Zubiri no niega a diferencia de los filósofos de la matemática que señalan el carácter empírico de las verdades matemáticas) se deben al modo de intelección propio de la matemática, o si los juicios matemáticos los tienen porque son propios de toda intelección campal en cuanto tal, sea del tipo que sea. Esta cuestión es crucial para decidir si la matemática es un modelo canónico de saber o no. La nivelación de la matemática con las ciencias de la naturaleza ha puesto en primer plano las cuestiones: ¿Hay evidencia en la verdad matemática? ¿Hay certeza de la verdad matemática? ¿Es posible hablar de rigor y exactitud matemáticas? La respuesta es que el carácter empírico de las verdades matemáticas lleva a negar estas cuestiones (por ejemplo Lakatos); o bien, si se quieren admitir hay que negar que las verdades matemáticas sean verdades de realidad y experiencia (por ejemplo Mac Lane). El planteamiento actual en términos incompatibles radica en que se supone, sin cuestionarse críticamente, que las verdades de las ciencias naturales no son evidentes, ni exactas, ni rigurosas, ni de certeza. ¿Es esto así? Lo primero que habrá que preguntarse es qué significa cada uno de los términos. Una vez más Zubiri llevará a cabo una conversión de estos términos desde una definición concipiente a su definición sentiente. El resultado es un enriquecimiento mayor, que permitirá aplicar estos mismos atributos a las verdades de las ciencias de la naturaleza con el mismo derecho a la aplicación de las verdades de la matemática. Sólo desde la inteligencia sentiente puede mantenerse el carácter empírico e histórico de la verdad racional matemática y, a la vez, las cualidades de evidencia, exactitud, rigor y de certeza de los juicios campales de la matemática. Y no sólo de la matemática sino de cualquier otra verdad del tipo que sea. La verdad matemática como tal verdad no conserva en la filosofía de la matemática zubiriana ninguno de sus "privilegios" anteriores, no es canon o paradigma de ningún otro tipo de saber. La aportación de Zubiri veremos, pues, que es sumamente original.

3. La verdad de Conformidad en la intelección matemática racional.

La conformidad de la verdad racional matemática a diferencia de la verdad campal es conformidad en encuentro y en cumplimiento, por ello más propiamente es verdad de confirmación. En esta cuestión está encerrado el debate también de suma actualidad de si la matemática es decubrimiento o creación, y si la verdad racional matemática es lógica o histórica Aunque esta última cuestión la haremos objeto de un apartado distinto.

 

2.1 Verdad real: fundamento de la Verdad de Conformidad.

 

La filosofía clásica, nos dice Zubiri, ha conceptuado la verdad desde inteligencia concipiente y ha pensado que la verdad se constituye en la referencia desde lo concebido o afirmado a una cosa real. Zubiri llama a esta idea clásica de verdad, verdad dual. Ciertamente, piensa el autor, la realidad es "verdadera" sólo respecto a una inteligencia. Pero ¿es radical y primariamente un respecto a la inteligencia en cuanto ‘concipiente’? La respuesta, nos dirá Zubiri, pende de cuál sea la función primaria y radical que se atribuya a la inteligencia. Y, según él, es aprehender las cosas reales como reales. Formar conceptos, concebir o idear, es una función ulterior. En la inteligencia sentiente, la verdad se halla en esa forma primaria que es la impresión de realidad. A esta verdad la denomina Zubiri verdad real. En ella no salimos de la realidad meramente actualizada. Una modalización de esta verdad radical es la verdad dual (en sus diferentes modos), pero que se funda en la verdad real. Caracterizamos, pues, en primer lugar la verdad real, base de todo el conocimiento en general y de la matemática en particular.

En el marco del constructivismo sentiente de la matemática, que se nos ha mostrado como un realismo transcendental, es perfectamente válida la afirmación noológica de Zubiri de que la realidad es el fundamento de la verdad. Esta consideración refleja el realismo de la verdad. Ya nos referimos a la realidad como donación, pues bien, la realidad se da a sí misma y da su verdad. La realidad se nos da junto con su verdad. En este aspecto el sujeto o la intelección es sentiente, esto es, receptivo. Esto es crucial. La realidad es lo que "da verdad a la intelección", Zubiri lo expresa diciendo que la realidad "verdadea" en la intelección.

"La realidad funda la verdad. La realidad es lo que da verdad a la intelección, al estar meramente actualizada en ésta. Y esta actualización es verdad porque envuelve la realidad. La realidad, pues, es lo que da verdad, y a este "dar verdad" es a lo que he solido llamar "verdadear". La realidad verdadea en intelección"[80]

Y, un poco más adelante, vuelve a insistir en el carácter real de la verdad, que permite no caer en un escepticismo,

" Verdad es realidad presente en intelección en cuanto está realmente presente en ella" [81]

Puede parecernos entonces que Verdad y Realidad son idénticas, y no es así porque hay realidades que no son verdades puesto que no están actualizadas en la intelección. La verdad es cualidad de la intelección, si bien no le añade nada distinto a lo real, por ello dice Zubiri que es mera ratificación del "de suyo" en que consiste lo real.

"La realidad es formalidad de la cosa, pero la verdad es cualidad de la intelección en cuanto en ella está presente lo real. Esta y no otra es la diferencia entre realidad y verdad: verdad real es ratificación de la realidad" [82]

La verdad real es real, en cuanto que en la ratificación tenemos lo real mismo, y es verdad, en cuanto que la ratificación es actualizante. Conviene recordar aquí que no se trata de la realidad allende la aprehensión sino que se trata de la realidad como formalidad del "de suyo" en que queda el contenido aprehendido. Zubiri define del modo siguiente lo esencial de la verdad real:

"He aquí la índole esencial de la verdad real: lo real está "en" la intelección, y este "en" es ratificación. En la intelección sentiente la verdad se halla en esa primaria forma que es la impresión de realidad. La verdad de esta actualidad impresiva de lo real en y por sí misma es justo la verdad real" [83]

LLegados a este punto nos haremos la siguiente pregunta: ¿Hay verdad real de los objetos matemáticos? Nos vemos obligados a hacer una serie de precisiones para ver cómo puede aplicarse la verdad real a la matemática. Cuando Zubiri habla de verdades reales es posible que tenga presente en su mente sólo las realidades "en y por sí mismas", únicas dadas en aprehensión inmediata de realidad, y, por consiguiente, que no esté aludiendo a los objetos matemáticos, puesto que no nos son dados de modo inmediato en aprehensión primordial de realidad. Entonces ¿cómo podemos hablar de verdades reales de los objetos matemáticos si no los aprehendemos por aprehensión primordial? Es admisible la verdad real de este vaso de agua que estoy aprehendiendo primariamente, sin embargo, no resulta claro cuál es la verdad real de un número imaginario que es una realidad no dada "en y por sí misma" sino que es una realidad postulada. ¿Cómo se puede hablar de verdad real de realidades postuladas? Esta pregunta con ser crucial ya no reviste suma gravedad, porque depende de esta otra: ¿cómo puede haber impresión de realidad de los objetos matemáticos? Y a esta ya le dimos respuesta en el sensismo de la matemática. Así pues, si hay impresión de realidad matemática no es ningún problema afirmar que hay verdad real matemática.

Explicitamos, no obstante un poco más cómo hay que entender la verdad real matemática. Este punto en Zubiri se halla implícito. Según nuestra interpretación, cabe decir que del mismo modo cómo el autor afirmaba que los objetos matemáticos son reales porque se postulan constructivamente en la impresión de "la" realidad campal dada por cualquier cosa real; así tenemos que afirmar que los objetos matemáticos tienen verdad real porque se postulan constructivamente en la verdad real de "la" realidad campal. La campalidad nos es dada en la aprehensión primordial de realidad junto con la impresión del momento individual de lo real. Y sólo porque es "más" que el contenido individual puede autonomizarse. El campo de realidad autonomizado es un ámbito transcendental, y en cuanto tal abarca las cosas reales concretas, por lo que se constituye en "medio". Según el autor, el medio es la verdad real del campo. Teniendo en cuenta que el campo es ámbito transcendental de realidad, su verdad, la verdad real del campo, es verdad real transcendental o es ámbito transcendental de verdad. Aquí está, según nuestro parecer, la verdad real de las matemáticas. A esta conclusión llegamos al constatar que Zubiri habla explícitamente no sólo de la verdad real de lo individual sino también que la realidad campal tiene su verdad real.

"...el medio no es, repito, sino un momento de la actualidad misma de lo real en cuanto real. El medio no es sino la verdad real del campo. El medio, pues, tiene por un lado, carácter fundado: está fundado en las realidades individuales; pero es por otro lado fundamento de esa unidad diferencial que llamamos "entre". El "ámbito transcendental", el campo, cobra así el carácter de "medio"[84]

Y un poco más adelante, insiste en que el medio es verdad real, verdad que tiene su origen en la aprehensión primordial de realidad, debido a que la verdad real de lo inmediatamente aprehendido compete no sólo a la verdad de su momento individual sino también a la verdad de su momento campal. Por tanto, la verdad real es indivisible, pero podemos hablar de dos momentos: la verdad real del momento individual de la cosa real "en y por sí misma", y "la verdad real de ‘la’ realidad del campo de ‘la’ realidad". Este segundo momento hay que tenerlo en cuenta para hablar de la verdad real de los objetos matemáticos.

"A su vez, el medio mismo es la actualidad física del momento campal de esa cosa real, de la aprehensión primordial, esto es, tiene su propia verdad real. Esta verdad real del medio no es sino la expansión de la verdad real del momento campal de la cosa aprehendida como real para poder juzgar de ella lo que es (en) realidad. De donde resulta, como ya dije, que el medio es verdad real: es la verdad real de "la" realidad del campo de "la" realidad".[85]

Dando el mismo tratamiento al tema de la verdad real matemática que Zubiri da a la realidad matemática (en este punto sí que lo hace explícitamente), creemos que puede afirmarse que la verdad postulada de la matemática se inscribe en la verdad real del medio de la realidad o verdad real de la realidad del campo de realidad. La razón, repetimos, es que la realidad matemática se inscribe en la formalidad de realidad dada en impresión de realidad en su momento campal, y consecuentemente la verdad matemática se inscribe en la verdad real de la formalidad de realidad en su momento campal, esto es, en la verdad como ámbito transcendental. Lo matemático es real, su realidad es la misma que la de cualquier cosa dada en aprehensión primordial; y lo matemático tiene verdad real, la misma que cualquier cosa aprehendida en aprehensión primordial. Lo que es distinto es el contenido de la verdad real. La condición de posibilidad de lo matemático no tiene nada que ver con el sujeto, por el contrario, es la realidad como ámbito y la verdad real como ámbito, y de los dos momentos el primario es la realidad como ámbito, es ésta la que funda la verdad como ámbito.

Aún es preciso otra matización en la verdad real de lo matemático equivalente a la del plano de la realidad. Veíamos que la realidad matemática se constituye en la formalidad de realidad en su momento campal, pero una vez realizada, por postulación constructiva, es algo "de suyo", tiene su propia realidad; tan es así que hay propiedades no deducidas ni puestas por mí que se me imponen y ello en cuanto que son algo "de suyo", son reales. En el plano de la verdad, que no es sino la actualización intelectiva de la realidad, es exactamente igual. En la verdad real como ámbito se constituye la verdad real de lo matemático; ahora bien, hay que decir que una vez constituido lo matemático, las nuevas propiedades reales nos dan su propia verdad real en la que nos movemos en toda ulterior intelección.

Aclarada la verdad real de la matemática veremos cómo es fundamento de la verdad dual. En primer lugar recordamos que para Zubiri la verdad dual se diferencia de la verdad real o verdad simple en que sale de la realidad, estableciéndose desde el concepto, la afirmación o la razón a la cosa real. Así tenemos respectivamente la verdad dual como autenticidad, como conformidad y como cumplimiento.

"Si volvemos a la cosa real desde su concepto, es la verdad como autenticidad. Si volvemos a la cosa real desde una afirmación, es la verdad como conformidad. Si volvemos a la cosa real desde su razón, es la verdad como cumplimiento" [86]

Zubiri considera que la verdad real es el fundamento de toda verdad dual. Y en este sentido lo real, en cualquier caso, da su verdad a la intelección, sea ratificando (verdad real), autentificando (verdad de autenticidad), veridictando (verdad de conformidad), o verificando (verdad de razón).

"Toda verdad dual se halla fundada en verdad real. En la verdad real, lo real está ratificando. En la verdad de autenticidad, lo real está autentificando. En la verdad de conformidad, lo real está veridictando; esto es, lo real está dictando su verdad. En la verdad de razón, lo real está verificando"[87]

Y continúa:

"Autenticar, veridictar, verificar son tres formas de modalizar dualmente la verdad real, es decir, la ratificación. Por esto, esta verdad real es, como veremos en su momento, el fundamento de de la verdad dual" [88]

La verdad de los juicios matemáticos (en la intelección campal) es, por un lado, coincidencia de los conceptos con lo real (en algunos casos será más que coincidencia porque se tratará de la propia constitución de los conceptos en la realidad, pero aún así será coincidencia con lo real como ámbito), y, por otro lado, es coincidencia de la afirmación con la realización de algo en la realidad de lo matemático ( también aquí en algunos casos será más que coincidencia propiamente constitución en el ámbito de lo real). En la intelección racional, la verdad dual es desde la razón a la cosa real. Es encuentro de algo que se busca, forjado ya intelectivamente y no un encuentro azaroso que fuera algo así como un choque o tropezón con lo real. El encuentro en cuanto tal es cumplimiento de lo que "podría ser", del fundamento, en lo que "realmente es". Es actualidad en cumplimiento, por ser algo buscado; si no fuera buscado no habría cumplimiento sino mera conformidad.

Por todo lo anterior queda puesto de relieve que las verdades matemáticas se fundan en la realidad, si bien es una realidad no dada en su contenido sino una realidad postulada en su contenido. En la verdad real se funda la verdad dual matemática. La verdad real consiste meramente en la ratificación del "de suyo" de lo real. La ratificación es la fuerza con la que se me impone impresivamente la realidad. No salimos de la impresión de realidad. En cuanto la realidad está aprehendida, está ratificada en la impresión misma, es verdad real. La verdad real nos tiene poseídos por la fuerza de la realidad, y no somos nosotros quienes la poseemos. Esta verdad real, dirá Zubiri, nos determina y, más enérgicamente, especifica que esta determinación es "un arrastre", la verdad real nos arrastra a ulteriores intelecciones.

"No poseemos la verdad real sino que la verdad real nos tiene poseídos por la fuerza de la realidad. Esta posesión no es mero estado mental o cosa semejante, sino que es la estructura formal de nuestra intelección ulterior misma. Toda forma de intelección ulterior a la intelección primaria y radical está determinada por lo real mismo: la determinación es entonces un arrastre. Estamos poseídos por la verdad real y arrastrados por ella a ulteriores intelecciones" [89]

La concepción zubiriana de la verdad matemática es la Teoría de la Conformidad de la verdad. Pero ¿significa esta Conformidad lo mismo que la Correspondencia o Adecuación de un enunciado con la realidad?, y, en consecuencia ¿se opone a la Teoría de la Coherencia (o Consistencia) y la Teoría pragmática de la verdad? Aplicar sin más estas concepciones a la postura zubiriana es muy peligroso porque su planteamiento es radicalmente distinto, y esto es lo que hay que aclarar.

El tema de la verdad se plantea tanto en la Teoría de la Correspondencia o Teoría de la Adecuación como en la Teoría de la Coherencia y Teoría Pragmática, partiendo de que la inteligencia y la realidad se hallan una "fuera" de la otra. Según la primera concepción esta separación es salvable; y según las otras esta separación es insalvable, es preciso, pues, sustituir la verdad como correspondencia por la verdad como mera consistencia en el propio pensamiento o por la utilidad en las consecuencias. Pero este planteamiento es, según Zubiri, radicalmente erróneo. Entre inteligencia y realidad, no hay exterioridad, no hay separación, no hay ruptura... sólo hay distancia "en" la realidad. La inteligencia está ya en la realidad. Zubiri parte de que la inteligencia está ya en lo real; la distancia no es distancia de la realidad sino distancia en la realidad. Por ello la coincidencia de la verdad dual consiste en salvar la distancia "en" la realidad misma. He aquí la concepción de la verdad en Zubiri: verdad como coincidencia, pero insistimos "en" la realidad en la que están inteligencia y realidad. Es coincidencia en la línea de la intelección misma, de la actualidad intelectiva de lo real en distancia. En palabras del autor:

"...la coincidencia es la unidad de la inteligencia y de la cosa en ese medio que es "la" realidad. La verdad como coincidencia es ante todo coincidencia de la afirmación y de la cosa "en" la realidad". [90]

La coincidencia entre la afirmación y la cosa real se establece en el medio de "la" realidad, que es la verdad real de la realidad campal. Afirmar es, según Zubiri, afirmar algo en la realidad, o "en verdad". No se afirma ni la realidad ni la verdad sino que se suponen.

" Contra lo que mil veces se ha dicho, hay que darse cuenta de que afirmar no consiste en afirmar la realidad, ni por tanto en afirmar la verdad, sino en afirmar algo "en la realidad", en afirmar algo "en verdad". Realidad y verdad son el supuesto medial e intrínseco de toda afirmación en cuanto tal. La coincidencia entre la inteligencia y lo real es una coincidencia que se establece en "la" realidad en que ambos términos son realidad verdadera: en la verdad real del medio. La verdad real del medio es así medio de coincidencia". [91]

Zubiri considera que la verdad como coincidencia es fásica, mientras que "la conceptuación clásica de la verdad no es fásica"[92] Esta sería pues una diferencia fundamental de su concepción respecto de la filosofía usual. Las fases de la verdad dual son, según el autor, tres:

1. La primera fase es la verdad de autenticidad que consiste en la conformidad de lo actualizado con la simple aprehensión:

"La autenticidad es la actualidad coincidencial como conformidad de lo real con mi simple aprehensión" [93]

2. La segunda fase es la verdad de conformidad de juicio, que consiste en la conformidad de la intelección afirmativa con la cosa real. Pero la cosa real, ya lo hemos dicho, no es para Zubiri una realidad externa o realidad transcendente a la intelección sino que es una realidad transcendental en la intelección misma. De otro modo, no podría haber conformidad de la inteligencia y lo real.

"No se trata, pues, de una conformidad entre una intelección ‘mía’ y una cosa que ‘por su cuenta’ anda por el cosmos. Esto sería dar lugar a una coincidencia ‘material’ y a lo sumo azarosa; pero la conformidad de que aquí nos ocupamos es en cambio una coincidencia constitutiva y formal... La coincidencia no se da formalmente más que en la actualidad intelectiva de lo real. Y esta actualidad no sólo no es ajena a lo real, sino que lo incluye"[94]

3. La tercera fase, es la verdad de cumplimiento, consiste en la conformidad de lo real con lo esbozado intelectivamente. Por eso no es mera conformidad como algo que se da sino que se ha ‘buscado’ intelectivamente.

"En este caso la confomidad no es mera confomidad sino cumplimiento, conforme a lo que se ha buscado y según se ha buscado... Es un tipo distinto de verdad: la verdad como cumplimiento. Es la tercera fase de la verdad". [95]

Comparando la Teoría de la Conformidad con las teorías clásicas, podríamos decir que de algún modo las incluye si bien desde la perspectiva original de Zubiri. La Conformidad, como la Correspondencia, es una coincidencia de la intelección con la cosa real, pero no al modo de una correspondencia única; por ejemplo varias geometrías incluso contrarias pueden coincidir con la realidad, porque no se trata de realidad transcendente. La Conformidad exige una unidad coherencial intelectiva, como la Teoría de la Consistencia, pero no exclusivamente al modo de la consistencia lógica sino unidad coherencial que hay que realizar y como tal es coherencia real (de ahí derivará la consistencia y no al revés). Y, por último, la Conformidad en la verdad de los esbozos racionales, como en la Teoría pragmática de la verdad, se logra por la verificación, en la casi totalidad de los casos, de las consecuencias, convergencias, y concordancias; pero a diferencia del pragmatismo no se verifica recurriendo al sujeto o comunidad científica, sino que es la realidad la que verifica en primera instancia.

Antes de finalizar este punto abordamos la cuestión ¿es posible el error?, ¿cómo se discierne el error de la verdad? Dice Zubiri que en la verdad real no es posible el error. La verdad, en este sentido, sería anterior al error. "Sólo respecto de la verdad dual es posible el error"[96]. El error en la verdad real vendría de identificar lo real en la aprehensión con lo real allende la aprehensión. Zubiri distingue entre la verdad como ámbito y la verdad como valencia. La primera es la verdad real del campo y es el medio de toda afirmación. La segunda es la cualidad en particular de cada afirmación en orden a la verdad como ámbito. Tanto la verdad como el error como valencias se fundan en la verdad como ámbito.

"La valencia de toda afirmación lo es en orden a la verdad como ámbito: la verdad medial es el fundamento de la propia verdad como valencia. Hay pues una diferencia entre la verdad como ámbito y la verdad como valencia. Como valencia se opone al error, pero como ámbito es el fundamento medial de la verdad y del error en tanto que valencias... el juicio verdadero envuelve la verdad como ámbito y la verdad como valencia". [97]

Creemos que esta consideración es válida igualmente para los juicios matemáticos. Su verdad dual se constituye en el medio de la verdad real del campo de realidad. Sólo habría que añadir que en este medio están incluidas además de todas las verdades de realidades tanto "en y por sí mismas" también las ya postuladas constructivamente por el pensamiento matemático en la realidad. Es un medio que se enriquece progresivamente.

Las dos valencias de la verdad en el juicio, fundadas en la verdad como ámbito, son la verdad y el error. Hay verdad cuando la actualidad exigencial de lo real en una dirección determinada, lo que Zubiri denomina parecer, coincide con la propia exigencia de repulsa o admisión de la cosa real respecto del parecer. Es la coincidencia entre la dirección intelectiva de lo que lo real "sería" en realidad y la dirección de exigencias de la actualidad de lo que lo real es "en realidad".

"La vía de la verdad es la vía según la cual es lo real lo que fundamenta el parecer. La vía del error es la vía según la cual el parecer fundamenta la realidad: la realidad sería lo que nos parece"[98]

La actualidad que la inteligencia intelige en la coincidencialidad es actualidad de lo real en sus dos momentos de estar presente y de prius (siendo "de suyo" lo que presenta). De ahí la posibilidad de comparar el juicio con lo real. El momento del prius en la actualidad "coincidencial" es decisivo para discernir la verdad del error.

"He aquí el fundamento de la discernibilidad del error y de la verdad: la actualidad coincidencial del prius en cuanto tal"[99]

 

2.2 Conformidad de la verdad del logos con lo real.

 

La conformidad del juicio matemático (y de cualquier tipo) consiste, como hemos visto, en la conformidad de la intelección afirmativa con la cosa real. Para que así sea la conformidad tiene que tener los caracteres de evidencia, rigor, exactitud y certeza. Examinamos cada uno de estos caracteres de la verdad del logos.

 

2.2.1 Evidencia matemática: ¿Es apodíctica?

Las verdades matemáticas en la filosofía clásica se consideraban generalmente como verdades apodícticas, frente a las verdades del resto de las ciencias que eran verdades asertóricas. El modelo de rigor y racionalidad era los Elementos de Euclides. A partir de unos axiomas, verdades evidentes, y unas leyes lógicas se iban deduciendo todos los teoremas con absoluta certeza. Con el descubrimiento de las geometrías "no-euclideas", el criterio de evidencia entró en crisis.

Actualmente está generalizada la actitud intelectual de cuestionarse: ¿las verdades matemáticas son evidentes? ¿qué tipo de evidencia: intuitiva o racional? ¿son evidencias inmediatas o mediatas?, ¿son verdades apodícticas?, ¿la evidencia matemática es el canon de toda evidencia?, ¿es más evidente el juicio matemático "dos más dos igual a cuatro" que el juicio "este libro está sobre la mesa"? Zubiri da respuesta, desde su perspectiva de inteligencia sentiente, a cada uno de estos interrogantes, empezando por ¿qué es evidencia?

¿Qué es evidencia? Esta es una cuestión clave[100] en la oposición y controversia entre las escuelas de fundamentación de la matemática: el formalismo (Hilbert) y el intuicionismo (Brouwer). La discusión consiste en decidir si la naturaleza de la evidencia matemática es racional (Hilbert) o intuitiva (Brouwer). Pero ¿qué es? Resulta escandaloso constatar que siendo tan importante esta noción en la delimitación de las dos escuelas, sin embargo, no se haya analizado más detenidamente en qué consiste. Zubiri llama la atención sobre la concepción errónea de la que se parte en la discusión de este problema epistemológico, y esclarece este término, desde su concepción constructivo-sentiente o realista transcendental.

La evidencia, nos dice, se ha venido considerando como un momento de la intelección, como un modo de inteligir algo. Y no es así. El determinante de la evidencia es la realidad. La evidencia es un momento de la realidad concreta actualizada en la intelección campal. La realidad funda la evidencia.

"... lo real de la aprehensión primordial de realidad es el determinante de la afirmación: esta determinación es e-videncia, es un ex. La evidencia es formalmente un momento de lo real actualizado en movimiento intelectivo"[101]

En el campo epistemológico de la matemática, se habla igualmente de evidencia intuitiva y de evidencia racional. Pero ello es señal de una idea vaga de evidencia. Según Zubiri, decir "evidencia intuitiva" es una especie de contradicción. La evidencia no es jamás un momento de la intuición, ni de lo que en sentido más riguroso llama el autor "aprehensión primordial de realidad", sino que es exclusivamente un momento del juicio, de la afirmación. Y es así porque la evidencia lo es de realización de simples aprehensiones en la cosa real aprehendida primordialmente. Supone pues la distancia entre la cosa real y las simples aprehensiones, porque lo que es evidente es que la cosa real sea esto o lo otro en realidad. La evidencia se funda en la exigencia de la cosa real aprehendida. Es un momento de la actualización de la realidad en el logos.

"sólo en el juicio hay evidencia. La evidencia es el principio determinante de la intelección mediada, del logos. ...Esta determinación lo es de la realización de la simple aprehensión en una cosa ya aprehendida como real. Y esa intelección es formalmente juicio y sólo juicio."[102]

La evidencia es la "visión exigencial" de lo que acontece en el juicio. Por ello sólo es posible por la dualidad entre simple aprehensión y cosa real, en definitiva por ser la inteligencia sentiente. En la aprehensión primordial no se da esta dualidad, sino que lo que está presente es la cosa real, tenemos la actualidad de la cosa real misma en su propia realidad. Es en el logos donde se da la dualidad: la cosa real ya aprehendida determina la intelección. Mientras que la evidencia es determinación, la aprehensión primordial es actualización . Y es imposible pretender que la actualización sea un modo de la determinación. En la aprehensión primordial de realidad no tenemos, pues, e-videncia (que sólo se da en el juicio) sino videncia, que es mucho más.

Esta definición zubiriana de evidencia, le lleva a admitir que todos los juicios son evidentes, en cuanto juicios, y no sólo los juicios matemáticos. En efecto, todo juicio tiene como momento suyo un determinante evidencial. Usualmente la evidencia de la realidad matemática se ha tomado como el canon exigencial de cualquier otro tipo de realidad, así lo ha entendido el "matematismo". Es preciso liberarse de la tiranía de este modelo paradigmático.

"No puede confundirse la evidencia de un orden con la de otro, y llamar inevidente a todo lo que no entra en la evidencia de un orden canónicamente establecido".[103]

La evidencia más que una propiedad es una línea en la que se está. De este modo, según Zubiri, el juicio no tiene evidencia sino que juzga en evidencia: la evidencia es exigencia videncial, y esto sólo es posible en un marco de libertad.

"La evidencia es una línea exigencial necesaria, pero trazada dentro de un ámbito de libertad; porque la intelección en movimiento es constitutivamente libre. Es una línea trazada en un espacio de libertad". [104]

La concepción clásica identifica evidencia y necesidad. Así cuando se afirma que la verdad matemática es evidente, se afirma que es necesaria y por tanto no puede ser de ningún otro modo. Zubiri, en cambio, además de mantener que es una vía o línea, nos dice que se traza en libertad. Es evidencia "cualificada por una orla de libertad". Es libre la referencia elegida, es creación libre el campo de simples aprehensiones, cuya realización en la cosa se va a afirmar con evidencia. También es libre la trayectoria que en orientaciones distintas puede conducir a la intelección. La determinación no tiene el sentido asignado por el determinismo ni tan siquiera en la matemática, que se tomó en esta concepción como el modelo canónico.

La filosofía clásica suele conceptuar los tipos de verdad en función de la conexión entre el predicado y el sujeto. Si la mente ve por simple inspección que el predicado pertenece al sujeto, la evidencia es inmediata. Si la conexión del predicado con el sujeto requiere de un tercer término distinto, la evidencia es mediata. Este término medio puede ser racional, y entonces la evidencia mediata se denomina verdad de razón. Y puede ser también que este tercer término sea de experiencia, entonces son las verdades de hecho. Zubiri considera inaceptable esta concepción, y aporta sobre la evidencia una concepción sentiente en lugar de ésta concipiente.

"Pero siempre se piensa que en una o en otra forma, todas estas evidencias mediatas se retrotraen a ciertas evidencias fundamentales, y en este sentido primeras. Y de éstas se nos dice que son evidencias inmediatas. No lo pienso así: no hay en el rigor de los términos ninguna evidencia inmediata" [105]

Se confunde, según Zubiri, el concepto de término intermediario y el concepto de medio. Y aunque no toda evidencia tiene un término intermediario sí que está apoyada constitutivamente en el medio de la realidad. En este sentido, no toda evidencia es mediata, pero sí que toda evidencia es mediada. No hay evidencias inmediatas.

"En primer lugar, nos habla de verdades de evidencia inmediata y de evidencia mediata. Y esta diferencia es inaceptable. Suele entenderse por evidencia inmediata aquella cuya verdad se funda en la simple inspección del predicado y del sujeto. Y esto no es así. Desde el momento en que la intelección es distanciada, su presunta conexión es esencialmente y constitutivamente una conexión que se da en un medio de intelección... La inmediatez se refiere a la carencia de un tercer término que establece la conexión; pero hay un medio y una mediación en la que esta conexión se establece. Haber confundido la inmediatez con la inmediación es un error cardinal"[106]

No hay pues diferencia entre verdades de evidencia inmediata y de evidencia mediata, todas hallan su verdad de la prioridad de lo real (momento del prius ) en su momento coincidencial con la afirmación de lo que sea en realidad la cosa ya aprehendida.

"Los llamados juicios primeros reciben su verdad de aquello mismo de que la reciben todos los demás juicios: de la actualidad coincidencial del prius, de la prioridad de lo real respecto del parecer en una misma actualidad intelectiva" [107]

La evidencia nunca nos es dada inmediatamente. Sólo nos son dadas las cosas reales, y lo son en aprehensión primordial. La evidencia siempre es un "esfuerzo". La evidencia no es del ser sino que es evidencia exigencial de lo real. La evidencia se funda en la realidad. Zubiri insiste continuamente en que la evidencia no es algo que se dé en el sujeto sino que es una exigencia que lo real mismo impone a la intelección. La cosa real es la que exige la realización de la simple aprehensión. En la evidencia Descartes y Husserl, según Zubiri, emprenden el camino desde la claridad hacia la cosa, y se trata de todo lo contrario de ir desde la cosa hacia su claridad. Lo propio de la evidencia es ser "visión exigida", es visión de lo que la realidad exige.

"... la evidencia es siempre noérgica, y es una exigencia impuesta por lo real, por la fuerza impositiva de la impresión de realidad." [108]

Por último, veamos la respuesta de Zubiri a la cuestión de si el juicio matemático "dos más dos igual a cuatro" es una evidencia apodíctica. Y, en general, ¿son evidencias apodícticas los juicios matemáticos? ¿Hay verdades apodícticas y verdades asertóricas? La discusión actualmente de estos problemas se plantea meramente en el plano lógico, pero hay que verlos desde el momento de "aprehensión de realidad de lo matemático". Esta es la perspectiva Zubiriana.

Antes de entrar en la distinción entre evidencia apodíctica y asertórica es preciso aclarar dos momentos de la evidencia que Zubiri denomina evidencia constituida y evidencia constituyente. La evidencia constituida es resultado, es la cualidad de lo inteligido o de lo visto. La evidencia constituyente es el momento radical y fundante; es dinamismo, sentiente, exigencial constituyente: es "evidenciación". La constitución de la evidencia no es un modo de actuidad sino que es un modo de actualidad.

Desde el punto de vista de la evidencia constituyente, ¿hay alguna diferencia entre evidencia asertórica y apodíctica? Zubiri lo niega. No hay evidencias asertóricas y evidencias apodícticas. La evidencia constituyente es en cualquier caso necesitante. Pero necesitante no es lo mismo que necesario. Sólo en el orden de las realidades "en y por sí mismas", esto es, de la "actuidad", pueden ser las realidades apodícticas o asertóricas; por ejemplo, es necesario que el fuego queme y, por el contrario, es contingente que este libro esté sobre la mesa. En la evidencia no se trata de actuidad sino de actualidad, y, por tanto, no se trata de necesario sino de necesitante. Del mismo modo que veíamos que no hay verdades necesarias y verdades contingentes sino que la verdad siempre es algo dado, y lo único que hay son verdades de realidades necesarias y verdades de realidades contingentes; así también no hay evidencias apodícticas y evidencias asertóricas, sino que todas las evidencias son necesitantes, y únicamente puede hacerse la distinción entre evidencias de realidades necesarias y evidencias de realidades contingentes.

"En cuanto evidencia no hay diferencia ninguna entre evidencia asertórica y apodíctica. La diferencia no se halla en la evidencia sino en la realidad de la cosa" [109]

Zubiri insiste en esta afirmación a través de un ejemplo que tantas veces se ha utilizado precisamente para marcar la diferencia entre los juicios matemáticos (apodícticos) y los juicios de hecho (asertóricos). ¿Es más evidente inteligir que "dos más dos son cuatro" que inteligir que "este libro está sobre la mesa"? Zubiri contesta que la evidencia de los juicios matemáticos no es apodíctica a diferencia de la evidencia de los juicios de las cosas reales "en y por sí mismas" que sería asertórica. En cuanto evidencias no se trata de necesidad sino de carácter necesitante. Y tan necesitante es la evidencia del juicio matemático como la del juicio de hecho. La aprehensión de "dos más dos" exige la realización del cuatro con idéntica necesidad a la aprehensión de que "este libro sobre la mesa" exige que sea afirmado así.

"La evidencia es siempre necesitante. Por muy fáctico que sea el que este libro se encuentre sobre esta mesa, es absolutamente necesario inteligir que está en esta mesa, tan necesario como inteligir que dos y dos son cuatro. La exigencia con que la intelección de dos más dos constituye la intelección de la realización del cuatro, no es una exigencia formalmente distinta de la exigencia con que este libro que está sobre la mesa exige que sea afirmado así. Es lo necesitante. [110]

Por último, hay que esclarecer que el carácter necesitante de la evidencia matemática, o del tipo que sea, nada tiene que ver con la relación lógica entre sujeto y predicado. En la concepción clásica se ha identificado la afirmación con el juicio predicativo, S es P, y se ha considerado necesario o apodíctico el juicio en el cual el sujeto lleva al predicado o viceversa. Ahora bien, además de que la afirmación no es siempre logos predicativo, Zubiri señala que el carácter necesitante de las afirmaciones no es conexión entre sujeto y predicado sino que la necesidad con la cosa actualizada en mi intelección nos lleva a la afirmación de ella. La exigencia de la propia realidad actualizada es la que confiere el carácter necesitante a toda e-videncia. Los polos del carácter necesitante de la evidencia están claros, pues, no se basan en la estructura lógica entre un sujeto y un predicado; necesitante no es necesidad lógica. El carácter necesitante se establece entre la realidad actualizada y la realización que llevamos a cabo determinada por ella; necesitante es la exigencia de la realidad actualizada para afirmarla de un modo u otro.

"Toda exigencia evidencial es constituyente, y la constitución misma no siempre es necesaria, pero es siempre necesitante. No se trata de la necesidad con que un predicado lleva a un sujeto, o de la necesidad con que un sujeto lleva a una predicado, sino que se trata de la necesidad con que una cosa real concreta (necesaria o contingente) actualizada medialmente en mi intelección, determina mi afirmación de ella"[111].

 

2.2.2 Rigor y exactitud matemáticas: ¿Es modelo canónico?

La división de ciencias exactas y ciencias naturales es clásica. En esta denominación ya va implícita la concesión de exactitud y rigor a la Matemática y su negación a las otras ciencias.

Actualmente los epistemólogos de la Matemática se cuestionan si la Matemática es la ciencia del rigor y de la exactitud, o más bien carece de ambos atributos como el resto de ciencias. Exactitud y rigor son dos cuestiones capitales que han jugado un papel fundamental en el dogmatismo, por eso mismo la necesidad de alejarse del dogmatismo parece implicar la negación de ambos. ¿Pero necesariamente el no admitir el dogmatismo matemático conlleva el rechazo de exactitud y rigor matemático? La respuesta depende, en primer lugar, de cómo se entiende estas nociones. Normalmente en esta discusión se sobreentiende sus significados y lo que se hace es conceptualizarlo concipientemente. Zubiri, desde inteligencia sentiente, arroja nueva luz sobre estos términos. Una vez examinada la cuestión ¿cuál es el carácter formal propio de la exactitud y del rigor?, podrá responder a estas otras preguntas: ¿son exactas y rigurosas las verdades matemáticas? Lo exacto del saber matemático, ¿cobra su fuerza de que sea matemático? ¿Son las evidencias matemáticas las únicas evidencias exactas? ¿Consiste la exactitud matemática en su rigor lógico? ¿Puede la matemática constituirse en canon de exactitud de las otras intelecciones?, ¿Puede seguir admitiéndose la distinción de ciencias exactas y ciencias naturales? ¿Es compatible el carácter empírico y el carácter de exactitud? Hemos visto que Zubiri considera las verdades matemáticas como verdades empíricas, pero ello no le lleva a negar el carácter de exactitud y de rigor, (como ocurre entre los filósofos actuales de la ciencia), al contrario enriquece y expande estas notas al dominio de cualquier verdad empírica. Si las verdades fueran relaciones de conceptos no podría hablarse de exactitud y rigor, porque son notas determinantes de la realidad actualizada en el logos, igual que veíamos en la evidencia.

La exactitud es propia del logos. Es resultado de la exigencia, digamos que es la imposición exigencial de la realidad ya aprehendida primordialmente. Por tanto, sólo la actualización diferencial, según Zubiri, tiene el carácter de ser "ex-acta", y no lo tiene, sin embargo, la aprehensión primordial de realidad.

"La exactitud es la cualidad de estar exigido. Es lo que no tiene la aprehensión primordial de realidad. Si se me permite el latinismo, diré que la aprehensión primordial no es "ex-acta"; sólo la intelección diferencial es ‘ex-acta’" [112]

Y continúa Zubiri haciendo hincapié en que el modo de intelección no es determinante de la exactitud de lo inteligido, sino que es justo lo contrario: es la cosa real la que determina la exactitud de su intelección. Y lo hace a través de sus exigencias en la intelección distanciada en "la" realidad. El realismo transcendental de la matemática sostenido por el autor le lleva a afirmar, pues, que la cosa real es fundamento de la exactitud de la intelección. Este giro en la epistemología matemática nos parece fundamental.

"En la incompacta oquedad de sus exigencias, la cosa real determina la exactitud de su intelección"[113]

La exactitud no es resultado del método seguido por el matemático sino que es resultado de la exigencia de la realidad. La cosa real nos da, en aprehensión primordial de realidad, junto con sus notas, un sistema de exigencias que en aprehensión diferencial se discriminan, en esto consiste la evidencia, y no en distinguir las notas.

"Porque la aprehensión diferencial no sólo está fundada en la aprehensión primordial sino que está formalmente exigida por ésta. La cosa real inteligida no es sólo un sistema de notas sino también un sistema de exigencias. Y el término formal de la evidencia es discriminación de exigencias, no distinción de notas"[114]

Pues bien, exactitud es atenerse a lo exigido, es estar contenido en los límites estrictos de la exigencia. Precisamente por estar la evidencia determinada por exigencia constrictiva, es por lo que toda evidencia es exacta. Rigor y exactitud son dos términos indisociables. La exactitud es rigor que viene exigido desde la cosa real. Sin rigor no hay exactitud.

Cada cosa y cada aspecto de ella tiene sus propias exigencias articuladas de un modo sumamente preciso. Al ser discriminante de exigencias, la evidencia queda contenida en los límites estrictos de lo exigido. Y en esta constricción es en lo que consiste la exactitud: es el rigor exigido por la realidad"[115]

Ahora bien, esta constricción que determina la evidencia matemática (o cualquiera), este rigor matemático (o del tipo que sea) se ha identificado con "rigor lógico". Es un signo más del logicismo de la matemática (y de la intelección en general). Según Zubiri esto es incorrecto en general, y lo es igualmente en la matemática. Cuando se habla en matemática de la revolución del rigor se refiere al rigor lógico. Las escuelas formalista y logicista sustituyen la intuición, que consideran vaga y sujeta a error, por el rigor lógico, único que puede proporcionarnos la verdad sin engaño. Desde la postura constructivista sentiente de la matemática vemos que efectivamente en la intuición (mejor sería decir en la aprehensión primordial de realidad) no hay rigor y exactitud, pero ella es la determinante del rigor y exactitud de la aprehensión diferencial y no el pensamiento lógico. No es correcto, pues, decir que en Matemática la exactitud es rigor lógico, lo que significa rigor es "constricción exigencial". A la logificación de la exactitud y rigor, Zubiri responde con el proceso inverso reifica la exactitud y el rigor. Son términos de un proceso sentiente: sentimos la constricción exigencial. Lo lógico es un mero procedimiento que constriñe la exigencia.

"Esta exactitud no significa, pues, ni tan siquiera en la matemática ‘rigor lógico’ sino ‘constricción exigencial’. Lo lógico es simplemente un procedimiento para constreñir la exigencia, y no al revés como si ser exacto fuera ser lógico"[116]

El constructivismo sentiente de Zubiri no es mero logicismo-formal, pero tampoco es mero intuicionismo; tanto la aprehensión primordial (intuición), como el logos (lógica) son momentos de la construcción matemática. Por eso, igual que hemos visto que niega toda reducción al logicismo, niega también toda reducción al intuicionismo. Y, en concreto, va a afirmar, en oposición a los intuicionistas, que el rigor y la exactitud no son un empobrecimiento de la intuición. Tan necesario es en el conocimiento contar con la riqueza de la intuición como con la exactitud de la evidencia, esto es, la intelección constrictivamente exigida por lo real. En Matemática (y en general) no basta con la intuición (aprehensión primordial), es preciso la exactitud y rigor de la intelección campal.

"El rigor no es la precisión, sino que la precisión es a lo sumo una forma de rigor. El rigor propio de la evidencia no es precisión sino exactitud: intelección constrictivamente exigida por lo real. La evidencia será y es más pobre que el contenido de lo intuido. Pero es inmensamente superior en exactitud. La intuición más rica jamás constituirá la mínima exactitud que necesita la intelección de una cosa "entre" otras. Por tanto la intelección ha de ser rica pero también exacta" [117]

Las cuestiones que nos formulamos al principio hallan, respuesta en este original enfoque de Zubiri. Nos preguntábamos si el saber matemático es saber exacto. No hay duda de que los juicios matemáticos son exactos, puesto que son juicios de realidad postulada, y como tal realidad tiene un sistema de notas y de exigencias que constriñen la intelección matemática. El resultado de este rigor es la exactitud. Rigor y exactitud son caracteres efectivamente de la intelección matemática. Pero su exactitud no estriba, por lo que se ve, en ser resultado de un tipo especial de intelección, como, en general, se ha considerado. No es el modo de intelección matemático el que determina la exactitud y el rigor, sino lo real actualizado en inteligencia sentiente. En palabras de Zubiri,

"La exactitud así entendida no se modela sobre ningún tipo especial de intelección que sirviera de canon para las demás. Por ejemplo, lo exacto del saber matemático no cobra su fuerza de que sea matemático, sino de que la evidencia es siempre exacta, esto es, de ser un saber en que lo sabido está estrictamente determinado por lo exigido" [118]

Frente al escepticismo que niega que la matemática sea ciencia exacta, hay que afirmar, desde la inteligencia sentiente, que toda ciencia es exacta, más aún cualquier intelección diferencial es exacta. Hay distintos tipos de exactitud y lo que no se puede hacer es medir todos por uno sólo, como así se ha hecho históricamente con la matemática. Hay que librarse del equívoco aceptado durante tiempo de tomar el saber matemático como canon de exactitud. Esto es lo que sugiere la aspiración de Husserl de hacer de la filosofía una ciencia estricta, como ya lo intentó uno de sus precursores, Descartes. Ahora bien, ser estricta ¿es seguir el canon matemático? No, cada saber y cada intelección, sea matemática o del tipo que sea, tiene su peculiar exactitud. Es inválida la distinción que planteábamos al inicio de este punto: ciencias exactas / ciencias naturales (y cualquier intelección diferencial no matemática). Tan exacta es la historia o la filosofía como la matemática. Todas las ciencias son exactas. Esta idea es auténticamente revolucionaria, mientras que en la epistemología matemática es un auténtico problema seguir afirmando que la matemática es ciencia exacta, Zubiri no sólo dice que la matemática es exacta sino que igualmente, sin titubeos, sostiene que cualquier intelección campal es exacta. Ahora bien, insistimos en que el término "exactitud" desde inteligencia sentiente no significa lo mismo que desde inteligencia concipiente. Y aclararlo es fundamental para no desviar la verdadera aportación de Zubiri.

"Por todo esto, todo saber, sea o no matemático, tiene su propia exactitud. La historia misma tiene su tipo de exactitud propia. Más aún, no sólo la ciencia es exacta sino que toda intelección diferencial, por elemental que sea, es exacta. Y justo por esto es por lo que la ciencia puede ser y es exacta: lo es por ser intelección diferencial" [119]

¿No nos lleva esta concepción a un dogmatismo ? Zubiri se adelanta a esta objeción haciendo notar que no se trata de algo que ya se posee definitivamente sino que es una línea por donde se camina. Hay aproximación.

"Naturalmente, vuelvo a recordar, la exactitud como la evidencia misma, es solamente una línea, la línea de exactitud. La intelección de la realidad "entre" está formal y constitutivamente en la línea de la exactitud. La intelección de la realidad "entre" está formal y constitutivamente en la línea de la exactitud"[120]

Y lo que es fundamental, Zubiri pone el rigor y la exactitud, implícitamente, en la línea de la conformidad, no en la adecuación. En efecto, si la verdad dual es coincidencial o conforme, creemos que se debe a que es rigurosa y exacta. Ahora bien, esto no dice nada respecto de la adecuación que es momento distinto del de la conformidad, como ya señalamos. El rigor y la exactitud no significan adecuación; es algo más modesto. Por tanto, no podemos confundir la afirmación de que los juicios matemáticos son exactos con la de que son adecuados. La adecuación es recubrimiento total de la realidad postulada y vimos que esto no es posible porque siempre surgen propiedades nuevas que las meramente definidas y postuladas (Teorema de Gödel), que alteran la estructura de lo real considerado en el conjunto total. Ahora bien, el conjunto fásico de los juicios exactos o con conformidad exacta constituyen momentos hacia la adecuación con la realidad postulada.

En definitiva, afirmar el rigor y exactitud matemática no supone aferrarse al "reducto dogmático", pero desde luego salva al conocimiento matemático de la confusión escéptica. Pensamos que puede decirse que en la intelección campal matemática (y en general) no conocemos lo real dado en impresión adecuadamente, porque la intelección campal es respectiva y este carácter siempre es abierto, sin embargo los caracteres que se inteligen son conformes con lo real. No inteligimos todo, mas lo que inteligimos lo hacemos exactamente. Por eso decimos que "dos más dos siempre será cuatro". Sí (dentro del mismo sistema de referencia). Pero cuatro no es una realización que recubra todas las exigencias de "dos más dos". Y de todos modos, cuanto hemos dicho, insistimos, se refiere a la intelección campal. En la intelección racional de la matemática no hay exactitud, aunque envuelve los juicios exactos.

 

2.2.3 Certeza matemática: ¿Se debe a su modo de intelección?

Zubiri, al ser consciente de que emprende una nueva vía o dirección en la filosofía de la matemática, analiza todos los conceptos claves de ella no admitiendo sin "conversión" a su marco conceptual constructivo-sentiente ninguno de ellos, puesto que le llegan de la tradición filosófica con una carga conceptual concipiente, o viciados por lo que denomina: logificación de la intelección. Esto lo hemos constatado ya con los términos: evidencia, exactitud y rigor; ahora lo veremos con el término certeza.

En la epistemología las nociones de duda, probabilidad y certeza son cuestiones claves, pues sobre ellas se constituye toda la controversia entre dogmáticos y escépticos que, según Lakatos, es "el tema básico de la epistemología". Ahora bien, ni el mismo Lakatos que se debate entre una postura y otra, para lograr establecerse en el falibilismo, se ha hecho cuestión de qué significan estas nociones, ni por tanto si falible es una noción del mismo orden que las nociones de duda, probabilidad y certeza.

Duda, probabilidad y certeza se han venido entendiendo como estados subjetivos de las afirmaciones sobre lo real. Esto es erróneo; según Zubiri, no son primariamente estados de seguridad o de inseguridad en mayor o menor medida, sino que son modos de afirmación que vienen determinados por los diversos modos de actualización de rasgos de la realidad en orden a la realización de las simples aprehensiones o a lo que es en realidad. Y esto es fundamental.

"En el modo-duda, no se trata primariamente de un estado de inseguridad en que quedamos afectados por la ambigüedad, a diferencia de otros posibles estados, como por ejemplo la seguridad, No se trata de estados, sino de modos formales de intención afirmativa. No se trata de que al afirmar lo ambiguo yo quedo en estado de duda, sino de que duda es la afirmación ambigua misma de lo ambiguo en cuanto ambiguo....Duda es pues un modo de afirmación, no un estado consecutivo a la afirmación"[121]

La diferencia entre los distintos modos de afirmación está en la firmeza con que actúa la fuerza de realización, que nos lleva desde la simple aprehensión a la actualidad de la realidad. El logos es sentiente porque siente la fuerza de realización y siente la distinta firmeza con que se realiza la posición, complexión o conexión de un juicio. Las diferencias de firmeza es lo que constituye los diferentes modos de afirmación. Pero la modalidad no es lo que lógicamente se ha conceptuado como diferentes modos de conexión del predicado con el sujeto: contingente, necesaria, etc. (logificación de la intelección). Es la realidad reactualizada en orden a las simples aprehensiones la que determina los distintos modos de afirmación. No es cuestión de lógica.

"... toda afirmación es en sí misma modal. Claro está, esta modalidad no tiene nada que ver con lo que en lógica se ha llamado clásicamente modalidad, a saber, la diferencia de la conexión del predicado con el sujeto según sea por ejemplo contingente, necesaria, etc. Aquí no se trata de la conexión de un predicado con el sujeto, sino del modo como afirme y según sea la actualización de las notas de lo real".[122]

Los distintos modos de afirmación están estructuralmente, no psicogenéticamente, apoyados entre sí. Así la estructura de la certeza se apoya en la estructura de lo que es la duda. Exponemos de modo gráfico los modos de afirmación o realización según los modos de actualización de lo real en orden a las simples aprehensiones. Nos centraremos sólo en la duda, la probabilidad y la certeza. Queda de manifiesto que los modos de firmeza penden de los modos de lo real actualizados diferencialmente.

 

La actualización		Los modos de afirmación o realización
indeterminación			ignorancia
	clarescencia	vislumbre
indicial	borrosidad	confusión	barrunto
	indicación	sospecha
ambigua			duda
	clinamen		sospecha
preponderante	gravedad	probabilidad	opinión
	vencimiento	convicción
obvia			plausibilidad
efectiva			certeza.

 

 

La duda es el modo de afirmación cuando la cosa real se actualiza con ambigüedad (no que pueda ser una cosa u otra , sino que a la vez se presenta como una cosa y otra, es modo del tanto-como).

"Duda es formalmente la afirmación de lo real ambiguo en cuanto ambiguo"[123]

La duda no es vacilar entre dos afirmaciones sino "un modo de afirmar lo que la cosa real es ambiguamente en realidad". Es saber que la cosa es ambigua en realidad respecto de mis simples aprehensiones.

"Vacilamos porque hay afirmación dudosa, pero no hay afirmación dudosa porque vacilemos. La duda es un modo de afirmación no es un conflicto entre dos afirmaciones"[124]

La probabilidad es otro modo de afirmación. Es un modo de opinión. La opinión es un modo de afirmación que consiste en afirmar preponderantemente lo que la cosa es en realidad. La probabilidad es un modo de afirmar en realidad lo real cuyos rasgos actualizados "cargan" de un lado más que de otro.

"La intención afirmativa de lo gravemente preponderante es la probabilidad".[125]

Por el contrario, si la cosa se actualiza no ambiguamente, ni preponderantemente, sino con efectividad unívocamente determinada, tenemos la afirmación cierta. Igual que en la duda hay que insistir en que: la certeza no es un estado subjetivo, lo que llamamos estar seguro, es algo referido a la cosa aprehendida y es que es así con firmeza total. Certeza pues no es estar seguro sino acertar, dar en el blanco. Este es el grado supremo de firmeza de la intención.

"La certeza es así el grado supremo de firmeza de la intención. Por lo mismo, podemos decir que es firmeza sin más, a diferencia de otros modos de afirmación tales como la duda o la probabilidad. La certeza no es la máxima probabilidad, como a veces suele decirse, sino que es otro modo de afirmar de distinta firmeza. En la certeza tenemos la firmeza por excelencia" [126]

Corrientes moderadas del positivismo lógico han querido identificar certeza con el máximo de probabilidad, pero esto es incorrecto. La probabilidad, ya lo hemos visto, es otro modo inferior de firmeza. La certeza, dice Zubiri, sólo se da en el juicio, no se da en la aprehensión primordial. El juicio cierto es una "confirmación" de lo que era la firmeza de la aprehensión primordial.

Este análisis zubiriano de los modos de afirmación según los modos de actualización de lo real, muestra que la certeza es el modo firme de realización de la simple aprehensión en la cosa real actualizada con efectividad unívocamente determinada. Y esto es aplicable tanto a los juicios matemáticos como a los juicios "físicos". Por ejemplo, si queremos inteligir el color que en realidad tiene esta cosa, y este color se me muestra en el movimiento intelectivo de mi aprehensión con efectividad unívocamente determinada como azul, afirmo con total firmeza que es azul, esto es, tengo certeza de que es azul. La diferencia, pues, entre las verdades de los juicios matemáticos y las verdades de los juicios "físicos" no consiste en decir que los primeros son ciertos y los segundos probables. Si los juicios matemáticos son modos de afirmación ciertas no se debe a ningún rigor lógico, o a que los predicados estén contenidos en el sujeto, o a que sean "a priori" o deductivos..., no, se debe a que la realidad postulada se presenta de modo efectivamente unívoca respecto de las simples aprehensiones. Pero esto no es exclusivo, ya lo hemos dicho, de los juicios matemáticos. Y, por supuesto, es errónea la tesis, compartida tanto por los neopositivistas como por los popperianos y Lakatos, de que la certeza es incompatible con el significado de los juicios. Según Zubiri, la certeza es una carácter del contenido de la intelección campal, (si bien no es del contenido de la realidad mundanal o realidad profunda). Es falsa, pues, en la intelección campal, la alternativa que pone Lakatos en boca de Kappa:

"si tu quieres que las matemáticas sean significativas, debes prescindir de la certeza. Si tu quieres certeza, elimina el significado. No puedes tener ambos. Gibberish está a salvo de refutaciones, proposiciones con significado son refutables por ampliación de conceptos". [127]

En conclusión, los modos de afirmación pueden ser la duda, la probabilidad, la plausibilidad... pero también la certeza. Este análisis original de Zubiri nos permite ver que las posturas epistemológicas: escéptica, falible y dogmática, responden a un planteamiento concipiente de los juicios. Por un lado los juicios se han entendido como conceptualización y por otra parte se ha partido de la ruptura de la cosa real y la intelección, y se ha entendido lo real como zona de cosas "allende" la aprehensión. Todo esto ha confluido en el planteamiento erróneo del problema de la certeza del conocimiento.

 

2.3 Conformidad de la verdad racional: en encuentro (momento lógico) y cumplimiento (momento histórico)

Hemos visto que la evidencia, rigor, certeza, carácter necesitante y exactitud, son caracteres de la verdad del logos. En ellos no hemos hecho intervenir el carácter histórico. No porque Zubiri niegue que la verdad matemática sea verdad histórica. Ni mucho menos puede entenderse su postura como ahistoricista. Pero la historicidad no es un carácter de la verdad del logos sino que es un carácter, según veremos, exclusivamente de la verdad de la intelección racional. La verdad racional matemática no es específicamente exacta, evidente, rigurosa y cierta, sino en cuanto que envuelve verdad del logos. La verdad racional matemática es específicamente verdad histórica.

Ahora bien, la historicidad de la verdad matemática ¿imposibilita el recurso a un fundamento del conocimiento? ¿Es incompatible con el carácter lógico de la verdad matemática? ¿Hay que sustituir la pregunta sobre el fundamento del conocimiento por la pregunta sobre el avance[128] del conocimiento?

En la actualidad hay una clara ruptura entre la concepción de la racionalidad meramente lógica de la matemática (ahistórica), y la racionalidad meramente histórica de la matemática (alógica). Ante esta grave situación intelectual, Hegel diría que se le impone a la filosofía inexorablemente una tarea: ¿cómo reconciliar el carácter lógico y el carácter histórico en la verdad racional matemática? Esta cuestión pasa por la unificación del carácter de libre creación y del carácter de descubrimiento de la intelección racional matemática. En la medida en que se subraya la concepción de la matemática como descubrimiento se acentúa su carácter necesario y universal, independiente del sujeto y de la historia, y por el contrario si se considera la matemática como libre creación, se le atribuye a la verdad un carácter histórico y contingente. Así lo expresa Camino. Cañón, quien en su obra La matemática: creación y descubrimiento, ofrece su concepción de la verdad matemática como verdad lógica y verdad histórica. A esta solución subyace la concepción que la autora tiene sobre la intelección de la matemática: es a la vez creación y descubrimiento. A modo de contextualización actual previa a nuestro análisis de la solución zubiriana, y dada la convergencia, en parte, que tiene con ésta, recogemos el planteamiento que hace la autora en la citada obra.

"Un modo fecundo de abordar el tema de la verdad de manera sintética es intentar responder a la pregunta ya analizada: "la Matemática ¿creación o descubrimiento?" Si la contestación a la pregunta es "descubrimiento", surgen inmediatamente cuestiones como: "Descubrimiento, ¿de qué?", ¿de un mundo de objetos preexistentes, de la estructura misma del mundo natural, de ideas innatas a la mente humana? Cada una de estas posibilidades de respuesta conlleva tratamientos diversos del tema de la verdad matemática.

Si la respuesta es "creación", el tema de la verdad requiere una fundamentación diferente. Pero las respuestas exclusivas dadas al dilema"creación o descubrimiento" no agotan las posibilidades"[129]

De forma esquemática presentamos la relación de estas dos cuestiones a la que alude en otros autores, y también su concepción.

 

Creación / Descubrimiento	Lógico /histórico
1. Platonismo: Las verdades matemáticas se descubren. Son verdades de objetos ideales y su carácter es eterno e inmutable. (Frege, Russell, Cantor, el primer Zubiri)	La verdad no depende de la historia y del sujeto.
2. Pitagórica. La verdad matemática se descubre no en un mundo ideal sino en la realidad	La verdad no depende de la historia y del sujeto
3. Innatismo. La verdad matemática se descubre en la medida que se toma conciencia de que está en la mente. (Leibniz)	La verdad no depende de la historia y del sujeto
4. La postura de Kant subraya la creación, pero "a priori"	Las verdades matemáticas no son independientes del sujeto humano pero no son históricas.
5. La concepción empirista: los objetos de la matemática son abstracciones de la mente, a partir de datos empíricos, son creaciones. ( J. S. Mill, W.O.Quine)	Las verdades matemáticas son históricas y contingentes. La experiencia puede refutar sus resultados.
6. La Matemática es simultáneamente descubrimiento y creación. Sólo cobran existencia al ser pensados, pero la construcción no es arbitraria. (C. Cañón)	La verdad matemática es lógica y es histórica.

 

 

La conciliación entre el carácter de descubrimiento y de creación de la matemática, le permite a la autora conciliar el contexto socio-histórico de la verdad con su expresión en un lenguaje que sigue unas reglas independientes de este contexto. Señala tres aspectos de la verdad: imposición de la realidad, necesidad lógica y carácter histórico (veremos que los tres aspectos son considerados por Zubiri, si bien con una unidad más radical). Dice Camino Cañón:

"La Verdad en matemáticas tiene tres caras: a) la propia de las relaciones entre los objetos (necesidad), b) la de las expresiones del quehacer matemático, histórico y falible, c) la verdad lógica —validez o consistencia— exigida en las teorías maduras"[130]

Nuestro interés en esta introducción, como ya hemos dicho, está en poner de manifiesto la enorme actualidad de la filosofía de la matemática de Zubiri, y la originalidad de la contribución que la línea de pensamiento abierta por el Constructivismo sentiente y transcendental, ofrece al problema de la verdad racional matemática. En su obra Inteligencia y razón (1983), laten estas dos cuestiones[131] fundamentales, apuntadas por Camino Cañón:

1. La primera que se plantea es la verdad racional de la matemática ¿es creación (libre construcción del sujeto) o descubrimiento (dado e impuesto al sujeto)?

2. Y, una vez contestada la anterior pregunta y en función de ella, en la última parte de su obra se cuestiona: la verdad racional de la matemática ¿es lógica o es histórica?.

La concepción zubiriana no es disyuntiva, sino que señala con total claridad el carácter indiviso de las dos perspectivas. En efecto, vamos a ver que para Zubiri la verdad racional tiene dos momentos: es encuentro de algo que se busca (Lógico) y es cumplimiento de un esbozo construido libremente (Histórico).

"La verificación es el verdadear de lo real en una intelección inquiriente, esto es en un esbozo. Verificar es encontrar lo real, es un cumplimiento de lo que hemos esbozado que lo real podría ser: en este encuentro y en este cumplimiento se hace actual (facere) lo real en la intelección (verum). Y en ello consiste la "veri-ficación’" [132]

Analizamos a continuación esta postura que consideramos de sumo interés para la actual epistemología matemática (y en general), primero atendemos a cada uno de los distintos momentos de la verdad: 1. La verdad como encuentro, 2. La verdad como cumplimiento, y seguidamente veremos la unidad de la verdad que es "pro indiviso" encuentro y cumplimiento, y, por consiguiente, su carácter "pro indiviso" es lógico e histórico.

 

2.3.1 Conformidad en encuentro de algo que se busca : carácter lógico.

La verdad racional, según hemos visto, es la tercera forma de verdad dual o verdad coincidencial (las otras dos son autenticidad y veridictancia). Su esencia es el encuentro. La realidad, en la verdad racional, está actualizada y verdadea en encuentro. La verdad racional envuelve, además de la verdad real, la verdad de autenticidad y la de veridictancia, pero en su modo peculiar de ser en encuentro. Así, pues, el encuentro es un modo irreductible a cualquier otro modo de verdad, y es un momento intrínseco de la intelección racional.

"La verdad coincidencial es ahora verdad en encuentro. Lo real está actualizado y verdadea en forma de encuentro. Esta verdad abarca ciertamente la autenticidad y la veridictancia, al igual que la veridictancia abarca la autenticidad. Pero esta intelección no es meramente autenticidad ni veridictancia, sino que consiste formalmente en ser autenticidad y veridictancia en encuentro"[133]

La verdad racional es siempre encuentro, según Zubiri, porque la razón, en cuanto sentiente, tiene carácter inquiriente. Inquiriencia es marchar inteligiendo o inteligir marchando. Y marcha es, a su vez, búsqueda intelectiva en la apertura de la realidad mundanal. Esta apertura es absoluta, de ahí que ninguna intelección la agote y que todo punto de llegada sea forzosamente nuevo punto de partida, como ya expresó bellamente S. Agustín y suscribe Zubiri.

"La inquiriencia, y por tanto el encuentro, pertenecen, pues, intrínseca y formalmente a la verdad en encuentro. San Agustín nos decía (De Trin., IX, 1): "Busquemos como buscan los que aún no han encontrado, y encontremos como encuentran los que aún han de buscar, porque cuando el hombre ha terminado algo no ha hecho sino comenzar’ " [134]

El carácter inquiriente de la razón tiene una importancia capital, y Zubiri insiste en ello, para comprender el carácter de encuentro de la verdad racional. Precisamente por no haber reparado en ello, la filosofía clásica, nos dice Zubiri, ha ignorado esta tercera forma de verdad, identificándola con la verdad de la afirmación. Y no es lo mismo conformidad sin más (autenticidad y veridictancia) que conformación en encuentro, la primera se da en la intelección campal y la segunda en la intelección mundanal.

"No es así; la inquiriencia es un modo de intelección, el modo de intelección racional, y la verdad es entonces no sólo conformidad sino encuentro. No es lo mismo afirmar algo sobre lo que está en el campo, que encontrar lo que eso que está en el campo es mundanalmente. No es lo mismo inteligir lo que algo es ‘en realidad’ que lo que algo es ‘en la realidad’. Es toda la diferencia entre conformidad y encuentro " [135]

La intelección inquiriente especifica cuál es la naturaleza del encuentro en la que consiste la verdad racional. Pone de manifiesto que el encuentro no es mero descubrimiento, entendiendo por tal un hallazgo de carácter fortuito, con el que nos hemos tropezado. No se trata en la intelección racional de este tipo de descubrimiento, sino que el encuentro es sólo y siempre encuentro de algo que se ha buscado. La verdad en encuentro es el mero término de la intelección en búsqueda. Por eso dice Zubiri que verdad racional es lo encontrado en búsqueda. Sin la búsqueda no habría encuentro, y esto es esencial. Por eso creemos que el autor prefiere el término encuentro al de descubrimiento. Al encuentro se le puede llamar descubrimiento porque es algo en cierto modo "dado", pero ya hemos advertido que no de un modo totalmente gratuito sino que exige el esfuerzo del intelecto. Por eso, más que "dado", lo exacto es decir que es logrado en lo dado. Si queremos hablar de diálogo, el encuentro es la voz de lo real dada a mi esbozo inquiriente. La dialéctica de la verdad racional es búsqueda y encuentro. En la apertura de la realidad mundanal la razón busca y encuentra. Lo encontrado es algo dado (con el matiz señalado) por la realidad misma. Recordemos que la realidad, según Zubiri, es algo que "de suyo" da, y da en cuanto que es abierta. La dimensión de la donación de las cosas es doble:

1. Las cosas dan que pensar. Es el momento de búsqueda.

2. Las cosas nos dan la razón de sí mismas. Es el momento de encuentro.

Dice Zubiri:

"Este momento positivo del ‘por-qué’ en cuanto encontrado es lo que precisa y formalmente constituye el ‘dar’. Que las cosas nos den la razón significa formalmente que su actualidad es actualidad encontrada en ellas mismas. Porque no se trata de un encontrar como algo azaroso, esto es, como si se tratara de un ‘tropezón’, sino que se trata del carácter formal de algo buscado, esto es de algo encontrado en búsqueda. Este carácter positivo es, por tanto, constituyente formal de la razón de las cosas: es justo el ‘dar’ de ellas" [136]

Si la intelección racional fuese un movimiento arbitrario o caprichoso de la razón, independiente de las cosas, no se explicaría cómo podría llegar a encontrar la verdad. En efecto el resultado al que llegan las concepciones que parten de que el pensamiento matemático es autónomo de la realidad, pura creación, es que no puede hablarse de verdad sino más bien de validez o coherencia formal. De ahí la importancia de insistir, desde el punto de vista zubiriano, en que la intelección en búsqueda (razón) no es una marcha espontánea, sino es un modo de intelección impuesto o dado por las cosas mismas. Su propio origen hace que la búsqueda esté orientada a ser encuentro en las cosas mismas. Como señalaba Camino Cañón, sólo una concepción realista de la matemática permite una concepción de la verdad como encuentro. Esto es lo que dice Zubiri: si no se parte de la realidad nunca se podría llegar a ella. ¿En virtud de qué? Para Zubiri, es la realidad aprehendida campalmente (sentientemente) en su modo de "hacia" la que desde y en ella lanza a la intelección "hacia" lo allende, esto es lo que constituye la intelección en búsqueda, en inquiriencia. La razón siente la realidad constrictivamente, y en ella marcha buscando y buceando lo que son las cosas en la realidad.

"En su virtud, la marcha es un movimiento dentro de la realidad para descubrir lo que lo real es en la realidad mundanal precisamente por la fuerza coercitiva de la realidad. Esta fuerza consiste en constreñirnos a que lo real que la razón busca sea inteligido como un contenido que no nos saque de la realidad" [137]

La búsqueda de la razón desde luego no consiste en lanzarse a la apertura mundanal a la expectativa de ver con qué se encuentra, esto sería tanto como "bracear en el vacío", y totalmente estéril. No se trata de esto sino que se marcha en búsqueda de algo muy concreto. La razón sí sabe lo que busca, lo ha forjado a modo de esbozo en su concepción intelectiva. Por eso el ¡eureka! significa ¡Al fin he encontrado lo que buscaba! y nuestra exclamación es más de júbilo que de sorpresa. En el encuentro lo real se actualiza verificando (o no) el esbozo de lo que "podría ser" lo real mundanalmente. Esto significa verificación: encuentro de lo buscado.

"Y como lo que se encuentra es o no es lo que se buscaba, resulta que lo real tiene ahora un modo de verdadear propio, un modo propio de actualización: es verificación" [138]

La conformidad en encuentro, según Zubiri, no es un acuerdo entre la afirmación esbozada y lo real. Es confirmación de lo inquirido y lo esbozado por lo real. No se tiene intelección racional independientemente del encuentro de lo esbozado. En la verdad racional lo real con-firma en encuentro la a-firmación del esbozo de lo que "podría ser".

"Toda verdad racional es búsqueda, es inquiriencia de algo que se ha esbozado. Y el encuentro no es simple conformidad de la afirmación esbozada con lo real, sino la "confirmación" del esbozo por lo real. Si no hubiera esbozo, no habría encuentro, ni por tanto intelección racional. Por esto es por lo que el encuentro es algo distinto del simple acuerdo de la simple conformidad" [139]

Lo real da firmeza a lo esbozado. Lo esbozado, recíprocamente, es firme "con" lo real encontrado. El encuentro, dice Zubiri, es confirmación constituyente de lo esbozado en y por lo real. Así la verificación matemática o com-probación consiste en la con-firmación del esbozo por la realidad. Es encuentro de "la realidad al hilo del "cum" de la verdad", aprehendemos la "realidad en verdad".

La con-firmación envuelve a-firmaciones, y si tenemos en cuenta que las afirmaciones son propias del logos, entonces, dice Zubiri, la verdad racional puede considerarse verdad de un logos, y en este preciso sentido, es verdad lógica. El autor aclara, encarecidamente, que no se trata de que la verdad racional matemática, o de otro tipo, esté fundada en la lógica (el Teorema de Gödel choca con este sentido). La esencia del logos matemático (y en general) no es afirmación predicativa, el considerarlo así ha sido resultado de la logificación de la matemática. El logos es un modo de actualización de lo real en el campo de la realidad. Hecha esta importantísima aclaración, dice Zubiri:

"En tal caso, verdad lógica significa verdad de lo real actualizado en logos. Entonces, evidentemente, la verdad racional es verdad lógica porque la verificación es un modo de verdadear dualmente que envuelve logos". [140]

Pero la verdad racional matemática no se reduce a verdad lógica, éste sólo es uno de los dos aspectos de la verdad racional matemática (o cualquiera), por el cual, según hemos visto, la intelección matemática envuelve afirmaciones, esto es actualiza lo real en logos. Este es el único aspecto tenido en cuenta en la filosofía de la matemática. Ahora bien, la verdad matemática, además de ser encuentro confirmante, tiene intrínsecamente otro aspecto: es cumplimiento de lo esbozado.

Vemos a continuación el segundo momento de la verdad racional de la matemática.

 

2.3.2 Conformidad en cumplimiento de lo real esbozado: carácter histórico.

En la verdad racional matemática (y en general) lo real da razón cumpliendo lo esbozado. La intelección del esbozo ya dijimos que es "construcción" de posibilidades posibilitantes, esto es, de lo que lo real "podría ser" en su realidad profunda. En cuanto libremente construidas, son posibilidades apropiadas en una libre opción. Lo encontrado es cumplimiento del esbozo. La verdad como cumplimiento consiste en la actualización de lo real en la intelección racional según mis posibilidades esbozadas. Lo real verdadea cumpliendo lo apropiadamente esbozado por la intelección. No es exacto hablar de la verdad como creación, porque verdad es el cumplimiento de esa creación. Zubiri no utiliza el término "creación" para designar la verdad como cumplimiento (como vimos que no utiliza el de "descubrimiento" para designar la verdad sino el de encuentro). Lo que impropiamente se dice verdad como descubrimiento y creación, Zubiri lo denomina verdad como encuentro y cumplimiento. No se corresponden unívocamente encuentro con descubrimiento, ni cumplimiento con descubrimiento. A cada término zubiriano le corresponde "a una" descubrimiento y creación. El cumplimiento es realización cumplida del esbozo.

"Este cumplimiento mismo consiste en realizar las posibilidades esbozadas y apropiadas. Por tanto esta actualización es lo que con todo el rigor semántico y etimológico del vocablo, debe llamarse actualización cumplida." [141]

La actualización cumplida, igual que la verdad en encuentro, no es mera conformidad (como la autenticidad y la veridictancia) sino que es confirmación. Este carácter de cumplimiento de la verdad es importantísimo, y sin embargo, no se ha tenido en cuenta en la filosofía de la matemática. Así, por ejemplo la afirmación de Lakatos: "lo que hay de interesante en matemáticas tiene carácter conjetural"[142], es verdad "a medias". Ciertamente toda verdad racional matemática es un esbozo libremente construido (si se quiere una conjetura) de lo que lo real en profundidad podría ser; pero el momento de verdad no está en la conjetura como tal, éste es otro momento del método distinto del de la verdad. El esbozo ha de conducir en su término al cumplimiento (o no) en la realidad, esto es a la verdad. Recordemos que el método del conocimiento, según Zubiri, tiene tres momentos distintos:

1. sistema de referencia

2. construcción libre de un esbozo

3. verificación: encuentro y cumplimiento de lo esbozado.

Lakatos, siguiendo a Popper, propone su método heurístico: conjeturas-pruebas-refutaciones. Según él la verificación es imposible. Sustituye en la matemática, al igual que Popper hizo en las ciencias empíricas, la verificación (hay que matizar que tal y como es entendida por el neopositivismo lógico) por la falsación. Lo único que podemos hacer es buscar refutaciones y mejorar nuestras conjeturas. Zubiri estaría de acuerdo con Lakatos en que es imposible verificar que un esbozo de posibilidades sea el único y que se verifique en sí mismo (y no más bien sus consecuencias, concordancias y convergencias); nunca llegamos a una verificación absoluta que detenga el regreso al infinito (todo punto de llegada sería un nuevo punto de partida). Admitido esto, no hay porqué negar la verificación, sino que se pone en evidencia que la verificación es de una razón sentiente, que como tal es inquiriente y esbozante, y la forma de actualizarse la realidad en ella es siempre actualidad problemática. Contando con todas las limitaciones de una inteligencia que es sentiente, pero ¿por qué no llamar verificación a la actualización cumplida como realización de las posibilidades esbozadas y apropiadas?.

Cumplimiento es realización de posibilidades posibilitantes y en este preciso sentido dice Zubiri que la verdad racional tiene carácter histórico. Abrimos un pequeño paréntesis para ver qué entiende el autor por historia, de modo que nos permita comprender el carácter de historicidad de la verdad racional. Veamos.

Esta cuestión es capital en el pensamiento de Zubiri. La conceptuación errónea de historia ha tenido graves consecuencias para el problema de la verdad matemática (y en general). La primera conceptuación[143] ha sido entenderla como un paso del no ser al ser. Esta noción como ruptura o discontinuidad, ha generado escepticismo e irracionalismo que se han aliado con el pragmatismo. Zubiri, paralelamente a la noción de potencia aportada por la metafísica de Aristóteles para solucionar el problema del movimiento, introduce la noción de posibilidad para dar cuenta de la novedad ontológica de la historia. Esta categoría le permite hacer la distinción entre hecho y suceso. Hecho es un acto, es la actuación de unas potencias. Suceso es la realización de unas posibilidades o de un proyecto por una libre opción, y, recíprocamente, opción es realización, cuando menos incoativa, de posibilidades. La raíz de la historia es la libertad. Se determina optando entre diversas posibilidades. La historia se hace por invención optativa. Inventar, dice Zubiri, es elegir. Realizar posibilidades es hacerlas mías, y en este sentido es una "apropiación". Toda opción tiene un momento físico de apropiación. La apropiación de posibilidades o actualización realizada de posibilidades es lo que constituye una acción en suceso. La historia está tejida no de hechos sino de sucesos. Es la actualización, el alumbramiento u obturación de puras posibilidades. El curso histórico no es simple "movimiento" sino "acontecimiento". La dialéctica histórica es dialéctica de posibilidades. La historia está próxima al acto creador, es cuasi-creación, porque consiste en producir la realidad, produciendo previamente su posibilidad. La historia está radicada en la inteligencia sentiente. Por ella el hombre es una esencia abierta al todo de la realidad. Y por serlo sentientemente, su apertura es procesual. Respecto a la matemática pensará Zubiri que es una posibilidad que nos hemos apropiado para entender la naturaleza. El éxito de esta apropiación no permite dudar de su valor positivo. Pero jamás sabremos si no hemos obturado con ello la apropiación de otras posibilidades que nos descubrieran aspectos insospechados de la naturaleza.

Pues bien, volviendo a la cuestión de la verdad racional caracterizada como cumplimiento, esto es, como realización de posibilidades esbozadas libremente, se entiende que Zubiri diga que la verdad racional es intrínsecamente histórica. La verdad racional no es un hecho sino que es un suceso. No se trata meramente del acto de nuestra facultad de inteligir, sino de una actualización media la posibilidad posibilitante.

"Como en la realización de posibilidades es en lo que consiste formalmente la esencia de lo histórico, resulta que, el carácter de la verdad racional en cuanto suceso es lo que constituye formalmente la esencia misma de lo histórico de esa verdad" [144]

Y continúa señalando que la verdad racional en cuanto actualidad cumplida es verdad histórica:

"Pues bien, la intelección racional por ser cumplimiento es formalmente histórica, puesto que cumplimiento es realización de posibilidades. La verdad racional tiene ese carácter de historicidad. La historicidad es un carácter intrínseco de la intelección racional, de la verdad racional"[145]

Zubiri sostiene que la verdad racional matemática es histórica en tres sentidos distintos, sin embargo hay que subrayar que los dos primeros le parecen obvios, y su aportación original está en el tercer sentido que es el que se refiere al carácter de la verdad racional esencial e intrínsecamente histórica (lo cual no ha sido señalado por la filosofía usual, por tener un concepto de historia extrínseco a la verdad misma). Veamos:

1. Afirma que la verdad matemática tiene historia. Esta consideración de que la verdad matemática pertenece a la historia le parece al autor una evidencia trivial. Se opone, pues, radicalmente al "ahistoricismo" característico del neopositivismo lógico. Éste es ahistórico precisamente porque es ciego para la dimensión creadora del conocimiento. Al limitarse a los enunciados lógicos de la intelección, el neopositivismo lógico olvida que la intelección es una construcción de un esbozo de posibilidades y que su realización es actualidad cumplida o histórica. Zubiri, desde su propia perspectiva, se une así a las voces antilogicistas y antiformalistas, que ponen de relieve la dimensión histórica de la matemática. Perfectamente suscribiría la crítica que Lakatos, con tono irónico, hace al formalismo ahistoricista.

"El formalismo desconecta la filosofía de las matemáticas de la historia de las matemáticas, puesto que, de acuerdo con la concepción formalista de las matemáticas, éstas no tiene propiamente historia.(...) Ninguno de los períodos "creativos" de las teorías matemáticas, y difícilmente alguno de los "críticos", habrían de ser admitidos en los cielos formalistas, donde las teorías matemáticas moran como los serafines, purgados de todas las impurezas de la incertidumbre terrestre"[146]

2. Afirma que la verdad matemática además de tener historia está socio-históricamente condicionada. Esto también es obvio para Zubiri, a pesar de que haya autores, es el caso de Karl Mannheim[147] (1893-194), que niegan[148] este carácter a las ciencias exactas (Matemáticas y Ciencias Naturales) a diferencia de las ciencias sociales. A continuación creamos la situación de un hipotético[149] diálogo cuyos interlocutores son Manheim y Zubiri.

Manheim expone su concepción de la Matemática como un producto intelectual totalmente desvinculado de su contexto socio-histórico a diferencia, por ejemplo, de la Historia.

"Del conocimiento de una proposición matemática no es posible leer cuándo y dónde fue pensado; en cambio, cualquier conocedor de la historiografía estará en condiciones de constatar cuando se le presenta cualquier dato de la historia, en qué época, desde qué punto de vista, desde qué voliciones culturales concretas, fue escrita la presentación puramente objetiva que se le presenta"[150]

Zubiri a este planteamiento respondería señalando que la Matemática, como cualquier otra ciencia, no escapa a su condicionalidad histórica. Que se considere extra-histórica y extra-mundana es la ilusión creada por el hecho de que sus verdades, a pesar de su condición socio-histórico, no son relativas sino objetivas. Pero son dos cosas distintas la condición y el valor de verdad.

"Olvidan que la función intelectual viene inscrita en un mundo, y que las verdades, aun las más abstractas, han sido conquistadas en un mundo dotado de preciso sentido. El hecho de que puedan flotar, sin mengua de su validez, pasando de un mundo a otro, ha podido llevar a la impresión de que nacen también fuera de todo mundo. No es así. La matemática misma se puso en movimiento, en Grecia, por la función catártica que le asignó el pitagorismo; más tarde fue la vía de ascenso del mundo a Dios y de descenso desde Dios al mundo; en Galileo es la estructura formal de la naturaleza. (...) Ninguna ciencia escapa a esta condición. Por esto, el hecho de que las ciencias adquieran un carácter extrahistórico y extramundano es índice inequívoco de que el mundo se halla afectado de interna descomposición" [151]

Respecto del avance de la Matemática, Manheim diría que es un proceso inmanente a la propia Matemática, según su desenvolvimiento lógico.

"Dos períodos cualesquiera de la historia del conocimiento humano sólo se distinguirían entre sí, por el hecho de que en el período anterior ciertas cosas eran todavía desconocidas y ciertos errores persistían aún, lo cual fue completamente corregido por el conocimiento posterior"[152]

Zubiri, en su turno de réplica, reafirmaría que en el desarrollo de los problemas matemáticos no se trata de una trayectoria inmanente, cuya coordenada consistiera en la mera lógica interna de la propia matemática, sino que para dar cuenta del desarrollo matemático hay que analizar la estructura total en que está situada la inteligencia humana.

"Aun en las más objetivas de las ciencias es innegable esta condicionalidad histórica. Hay problemas que tan sólo se plantean en ciertas épocas; inclusive problemas, planteados y resueltos, tal vez por azar, en una época, quedan aislados en la ciencia porque su estado histórico no permite darles sentido. El sistema de preguntas nace de la estructura total de la situación de la inteligencia humana"[153]

Hay muchos ejemplos que dan la razón a Zubiri, a la vez que se la quitan a Manheim. Uno de los más recordados por los distintos autores es el condicionamiento histórico que obstaculizó a Saccheri (1667-1733) la solución del "problema de las paralelas" o al quinto postulado de la Geometría de Euclides. A este ejemplo recurre Camino Cañón[154] para apoyar la misma tesis que ahora nos ocupa:

Los trabajos de Saccheri fueron realizados en el siglo XVIII bajo los criterios culturales y epistemológicos de que la Geometría de Euclides era el modelo único y perfecto del mundo físico, y que sus postulados y teoremas eran absolutamente verdaderos. Saccheri, leído retrospectiva-mente, nos ofrece el ejemplo de alguien que, habiendo tocado un resultado genial, lo rechazó porque las condiciones epistemológicas de las que él participaba le hacían imposible aceptarlo como correcto" [155]

3. Zubiri, además de señalar que la verdad tiene historia y que está históricamente condicionada, señala que la historicidad es un carácter intrínseco y formal de la verdad matemática misma. Esta es su aportación original: introducir la historia en la esencia misma de la verdad. La verdad racional matemática (y en general) es constitutivamente histórica. Y esto porque es actualización cumplida, esto es, realización de posibilidades esbozadas. No porque su objeto sea histórico o porque sea un acto intelectivo. Según Zubiri:

I. Es falsa la concepción de que la verdad racional histórica es verdad de algo histórico. No toda realidad en cuanto tal es histórica. Si así fuera la matemática no sería histórica porque su objeto en sí mismo no es histórico, como tampoco lo es un astro.

"Unas galaxias, un astro, un objeto matemático no son realidades históricas en cuanto realidades. Por tanto cuando lo real es histórico la vedad racional es doblemente histórica: es histórica porque lo real en este caso es algo histórico y es además histórica por ser una actualización racional. Sólo esto segundo es lo propio de la verdad racional en cuanto verdad" [156]

II Es falso que las verdades son históricas porque son actos que dependen del inteligir mío propio. Zubiri afirma que la intelección no tiene porqué ser histórica y aunque así fuera esta historicidad sería extrínseca al contenido de la propia verdad. No se trata para el autor de historicidad de nuestras acciones de inteligir sino de historicidad como modo de actualidad de la verdad.

Concluyamos insistiendo en que historicidad, según Zubiri, es actualidad cumplida. Esta definición constituye una pieza clave en la epistemología matemática zubiriana. Arroja nueva luz sobre el problema de la relación Verdad— Historia, y como vamos a ver entre Lógica— Historia en el problema de la verdad matemática.

 

2.3.3 Unidad de la verdad racional matemática.

Hasta aquí hemos analizado por separado los dos aspectos de la verdad matemática (y en general): 1. La verdad es encuentro: verdad lógica, y 2. La verdad es cumplimiento: verdad histórica. En este punto pondremos de manifiesto en qué consiste,según Zubiri, su unidad. Del mismo modo como la intelección racional de la matemática no es a la vez sino a una creación y descubrimiento — es lo que indica el término construcción sentiente —; y que su objeto no es a la vez sino a una realidad y construcción —es lo que indica el término construcción transcendental —; así la verdad no es a la vez sino a una encuentro y cumplimiento —es lo que indican los términos encuentro cumplido y cumplimiento encontrado —, y, por último, la verdad no es a la vez sino a una lógica y histórica —es lo que indican los términos lógica históricamente y histórica lógicamente—. Por tanto, no se trata de disyunción, pero tampoco de conjunción, sino de unidad "pro indiviso". Esta es la diferencia entre la solución zubiriana al problema de la verdad y la que, por ejemplo, nos ofrece la autora de Matemáticas: creación y descubrimiento, Camino Cañón, quien dice:

"¿Lo crea o lo descubre? Encontraríamos razones para justificar ambas respuestas. ¿No será entonces que este modo de plantear las cosas es un falso dilema? ¿No será entonces que este modo de plantear las cosas es un falso dilema? ¿No será más bien que la "creación matemática" sólo es creación cuando puede ser a la vez descubrimiento?"[157]

Desde la perspectiva zubiriana ésta no es errónea, pero no es exacta. Esta postura de Zubiri, que puede parecer mera sutiliza, no lo es y lo cierto es que abre una vía que a nuestro juicio es totalmente original. Su novedad del modo más simple la exponemos esquemáticamente:

 

Autores	Naturaleza de la Verdad matemática	Carácter de la Verdad matemática
Lakatos:	Creación	histórica
Frege:	Descubrimiento	lógica
C. Cañón:	Creación y Descubrimiento	lógica y histórica
Zubiri:	Encuentro cumpliendo Cumplimiento encontrando	lógica históricamente histórica lógicamente

 

 

2.3.3.1 Verdad: Encuentro cumpliendo y Cumplimiento encontrando.

 

La verdad racional matemática es "pro indiviso", "a una", encuentro y cumplimiento. Son dos momentos codeterminantes. La unidad recae en la propia realidad que es fundamento de la verdad racional. Lo real es "encontrado cumpliendo" y, recíprocamente es "cumplido encontrando"; lo real "confirma posibilitando" y, recíprocamente, lo real "posibilita confirmando". En la verdad racional, en definitiva, lo real verdadea de un modo peculiar: en "confirmación posibilitante" e idénticamente en "posibilitación confirmante".

"Como verdad de intelección inquiriente, la verdad racional es verdad en esbozo. Y la verdad de un esbozo es verificación, esto es, consiste en que lo real verdadea, en que lo real da verdad, en intelección esbozante. Esta verificación es encuentro y cumplimiento. Pero no según una "y" copulativa, sino de un modo radical en cada uno de esos dos momentos" [158]

Y sigue exponiendo la unidad indivisa de los dos momentos de la verdad:

"Lo real en esbozo es encontrado cumpliendo, y es cumplido encontrando. Encuentro es confirmación, y cumplimiento es posibilitación. Por tanto, se confirma posibilitando y se posibilita confirmando. Lo real verdadea en confirmación posibilitante y en posibilitación confirmante. En la identidad de ambas fórmulas consiste la unidad de la verdad racional" [159]

 

2.3.3.2 Verdad: Histórica lógicamente y Lógica históricamente.

 

La unidad de encuentro y cumplimiento determina la unidad de logicidad y historicidad. En efecto, logicidad y historicidad son dos momentos indivisibles y codeterminantes mutuamente en la verdad racional matemática. Cada término envuelve al otro pro indiviso. Lo lógico de la verdad matemática consiste en cumplimiento histórico y, viceversa, lo histórico de la verdad matemática consiste en encuentro lógico. La verdad racional es "lógica históricamente" y es "histórica lógicamente". Es lógica cumpliendo y es histórica encontrando.

" La verdad racional, es como hemos visto lógica y histórica. Pero esta "y" se presta a un fatal equívoco. Porque podría pensarse que la verdad racional es "a la vez" lógica y histórica. La "y" sería en tal caso una "y" copulativa. Esto no es del todo falso pero no es exacto. Porque la verdad racional no es "a la vez" lógica y histórica, sino que es pro indiviso, esto es "a una" verdad lógica y verdad histórica. Logicidad e historicidad son los dos aspectos no solamente indivisibles, sino mutuamente codeterminantes de la unidad de la verdad racional. La "y" significa pues unidad intrínseca indivisible" [160]

Y un poco más adelante insiste en este carácter codeterminante de los dos momentos de la verdad racional. La verdad racional matemática (y en general) es lógica históricamente y es histórica lógicamente.

"Cada uno de los dos términos (historicidad y logicidad) envuelve intrínseca y formalmente al otro pro indiviso. Esto es, la verdad racional es lógica históricamente (cumpliendo), y es histórica lógicamente (encontrando). Tal es la unidad intrínseca y formal de la verdad racional" [161]

¿Dónde hay que buscar la raíz última posibilitante de la unidad intrínseca, "pro indiviso" lógico-histórico y histórico-lógico de la verdad racional? Tocamos con el dedo toda la diferencia entre una razón concipiente y una razón sentiente. La unidad intrínseca de razón-sentiente es la que justifica la unidad lógico-histórica (o histórico-lógico) de la verdad racional. Toda verdad racional, matemática o de cualquier tipo, es lógico-histórica porque la propia razón es lógico-histórica o histórico-lógica. Y la razón es lógico-histórica por ser razón inquiriente y esbozante, y esto, en último término, se debe al carácter sentiente de la razón. La unidad de la razón sentiente es la que justifica la unidad lógico-histórica de la verdad racional. En la razón sentiente la realidad siempre se actualiza como pro-blema, esto es como actualidad campal "hacia" lo profundo; y este carácter problemático de lo real actualizado ( y no meras cuestiones mentales) es lo que determina el esbozo inquiriente de la medida de lo real en el mundo de la realidad, y precisamente por esto es lógico-histórica. En la actualidad de lo real como "pro-blema" en la razón sentiente es en lo que consiste la identidad lógico-histórico de la verdad racional. Sólo una filosofía sentiente de la matemática nos conduciría a estos resultados.

"En su virtud, la intelección racional es intrínsecamente lógica y histórica, precisa y formalmente porque es intelección de razón sentiente, esto es porque es la actualidad de la realidad mundanal como problema" [162]

Gráficamente:

 

 

 

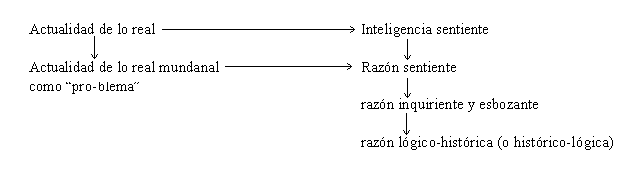
2.4. Constructivismo matemático: Historicismo lógico o Logicismo histórico

 

La unidad de la verdad nos aboca a la tesis zubiriana de que el constructivismo matemático (o cualquier intelección racional) es, intrínseca y formalmente, lógico-histórico, o histórico-lógico.

Ahora bien, afirmar que el constructivismo matemático es lógico-histórico ¿desemboca en un historicismo? El historicismo es un relativismo en tanto que considera que el conocimiento y su verdad es más o menos relativa al momento del decurso histórico en que tiene lugar. ¿Pero son contradictorias la verdad y la historia como pretende el historicismo? Zubiri considera inadmisible este punto de vista. Siempre rechazó el historicismo como tal. En Cinco lecciones de filosofía reconoce la condición histórica de la matemática, pero no le lleva a la renuncia de la verdad objetiva.

"Toda ciencia, incluso la matemática está sometida a una condición histórica de hecho pero la verdad de las teorías matemáticas no pende de esa condicionalidad histórica. Recíprocamente, el estudio de esta condicionalidad jamás podrá arrojar la menor luz sobre la verdad objetiva. De razones históricas sólo pueden resultar consecuencias históricas."[163]

En Inteligencia y razón vuelve explícitamente a alejarse del historicismo.

"Por tanto, afirmar que todo conocimiento es intelección lógico-histórica no es ni remotamente lo que suele llamarse historicismo"[164]

En primer lugar hay que precisar el sentido que se da a la historia, porque, según hemos visto, en el pensamiento de Zubiri no se trata de la historicidad del conocimiento y de la verdad como decurso sino como un carácter intrínseco del propio conocimiento y verdad en cuanto son actualidad cumplida. Además, es actualidad cumplida en encuentro, esto es, tiene carácter lógicamente verdadero. La intelección matemática es histórica en cuanto es lógicamente verdadera. La verdad más alta no queda empañada de arbitrariedad o relatividad, como en el fondo parece sugerir la postura de Lakatos. La historicidad no anula la verdad. Zubiri resuelve el problema de historicidad-verdad, historicidad-lógica de una forma original y fecunda, que va a la raíz misma: historicidad-razón.

Camino Cañón también defiende en Matemáticas: creación y descubrimiento, la historicidad del conocimiento matemático, pero compatibilizándolo con la verdad lógica del mismo. Y una concepción similar es la que el filósofo Eduardo Nicol sostiene en su obra Principios de la Ciencia. Para este autor la verdad y la historia no son contradictorias. La verdad de la ciencia es verdadera e histórica a la vez : histórica como creación, verdadera como representación objetiva.

"La verdad de la ley es verdadera y es histórica a la vez; histórica como creación, verdadera como representación objetiva"[165]

Zubiri no diría "a la vez" sino "a una". El conocimiento matemático es a una "histórico y lógico". Esta noción del conocimiento nos lleva a denominar su constructivismo lógico-histórico y histórico-lógico. Se opone a dos concepciones opuestas:

1. Al logicismo a-histórico (neopositivismo lógico, logicismo, formalismo, etc.) dominante en la primera mitad del S. XX, y

2. Al historicismo a-lógico (Lakatos, Wilder, etc.) dominante en la segunda mitad del S. XX.

En Matemáticas (y en general), según Zubiri, no se trata de una racionalidad lógica (que imposibilita la historia) ni tampoco de una racionalidad histórica (que imposibilita la verdad) sino de racionalidad lógico-histórica, esto es, racionalidad sentiente. Desde razón sentiente, es posible una filosofía de la matemática que evita tanto el puro logicismo: logicismo-ahistórico, como el puro historicismo: historicismo-alógico. El constructivismo sentiente y transcendental de la matemática es un logicismo-histórico y un historicismo-lógico. Mientras que el logicismo (porque desconecta de la realidad) y el historicismo (porque desconecta de la necesidad lógica y real) imposibilitan la verdad y generan un cierto escepticismo[166] perjudicial para el conocimiento entero, el nuevo constructivismo matemático, por el contrario, la posibilita eliminando el puro arbitrio.

El constructivismo sentiente y transcendental de la matemática es, pues, un logicismo cumpliendo y es un historicismo encontrando. Utilizando las categorías kantianas, podría decirse que el logicismo histórico (en cumplimiento) no es un logicismo vacío, ni el historicismo lógico (encontrando ) es un historicismo ciego. El verdadero avance del conocimiento matemático puede entenderse desde el Logicismo histórico o del Historicismo Lógico del conocimiento. Y esto mismo da cuenta de la Incompletitud de la Matemática.

Según nuestra interpretación de Zubiri, podemos decir que la resistencia que la realidad matemática ofrece al hombre le posibilita y fuerza a entenderse a sí mismo, a darse cuenta de "donde está". Es el auténtico choque con la realidad la que lleva a examinar las concepciones desde las que parte para aprehenderla. Y en este proceso, según sea la índole del choque, así es también el tipo de posibilidades que al hombre presente se le convierten en problema. No todo choque presenta la misma gravedad. Por ejemplo, Gödel intenta probar la completitud de la aritmética. No puede ser, la realidad aritmética se le resiste; este choque es de tal gravedad que conmociona la concepción lógica de la matemática, y Gödel se ve forzado a abandonarla. La insuficiencia de nuestros conceptos se hace patente. Al vernos obligados a superar la concepción anterior de la matemática podemos pensar que lo anterior era erróneo y sin valor para el presente. Sin embargo, esta manera de conceptuar la historia es concipiente. Lo cierto es que la intelección que nos lega el pasado nos procura un brinco más eficaz al futuro.

La historia de la matemática desde inteligencia concipiente resulta un tejido de hechos teóricos, pero vemos que desde inteligencia sentiente no se trata de esto sino de un tejido de sucesos teóricos. No se trata de hechos y de movimientos, sino de sucesos y sucesiones, acontecimientos y aconteceres. Por opción libre realizamos un sistema de posibilidades o un esbozo de lo que lo real "podría ser". Su apropiación es lo que constituye una acción en suceso. El hombre, en virtud de su inteligencia sentiente, tiene que optar por alguna posibilidad para probar si se realiza en la realidad campal. Las verdades matemáticas, por ser históricas, alumbran u obturan posibilidades. La dialéctica de la historia de las matemáticas es la dialéctica de posibilidades. La historia matemática no es un desarrollo lógico inmanente o un des-velamiento progresivo sino que es cuasi-creación.

La historia matemática es una continuidad[167] de posibilitación. Es un proceso porque cada momento no sólo viene después del anterior, sino que está apoyado en él, y, segundo, es un proceso de posibilitación; un proceso en que cada posibilidad se apoya en la anterior. Cada momento procede-de y precede-a, son los momentos constitutivos de todo proceso. La historia es un momento procesual.

Nuestros conceptos matemáticos tienen su propia historia. Recordemos que para Zubiri, son intelecciones constructivas. Un concepto es una construcción sentiente. Podría pensarse que la construcción del concepto tiene un carácter acabado en su propia génesis constructiva y en adelante se trataría de la aplicación del concepto constructo a nuevos objetos. Es lo que pensó Kant, desde su constructivismo sensible. Según Zubiri eso no es así. Precisamente porque los conceptos no son "puros" y "abstractos" sino "sentientes", es por lo que están en apertura continua a las realidades. La dialéctica de los conceptos no es una simple aplicación ni una ampliación a diversas regiones de objetos, sino una progresiva constitución del ámbito mismo del concepto, posibilitada, a su vez, por el progresivo descubrimiento de nuevos objetos o regiones que obligan a rehacer ab initio el sentido mismo de los conceptos, conservándolos y a la vez absorbiéndolos en una unidad superior.[168] Los conceptos matemáticos al ser realidades en concepto están sumidos en la dialéctica de la realidad igual que lo están los conceptos metafísicos. De este modo cuando se descubre (o se construye sentientemente) un nuevo objeto matemático se descubre (o se construye sentientemente) una nueva ratio entis, esto es, una idea previa que da pie para formar el nuevo concepto. En la constitución del concepto se conserva el contenido del concepto, pero subsumiéndolo en una ratio nueva y más amplia. Nos parece que es correcto aplicar a la matemática la afirmación zubiriana "La dialéctica ontológica es, ante todo, la dialéctica de estas rationes" [169] Si bien los vocablos "ontológica" y "ratio" no los conserva Zubiri posteriormente en la Trilogía de la intelección, pensamos que el sentido de lo expresado sí. La realidad en concepto matemática tiene su propia dialéctica que fuerza a re-construir los propios conceptos. No están los conceptos en un plano puramente lógico que les resguardara de estas modificaciones necesarias que se dan en su respectividad con las realidades. A la luz de una nueva ratio entis todo adquiere nuevo sentido, sin dejar de ser lo que era antes.

Conceptos, proposiciones y expresiones, afirma Zubiri, no son algo lógicamente determinado. Para que podamos conocer no basta con enunciados de sentido unívoco, porque en el conocimiento no se trata de llegar a una constatación "unívoca" con conceptos y expresiones precisos y exactas sino de emprender una dirección "fecunda" hacia lo real mundanal. Y es posible que con conceptos y expresiones que no están unívocamente realizados en una representación tracemos no obstante una dirección fecunda. Los conceptos y expresiones tienen como función principal lanzarnos hacia una creación nueva.

" El conocimiento no es un sistema de conceptos, proposiciones y expresiones. Esto sería un absurdo conceptismo, mejor dicho un logicismo en el fondo meramente formal. Y además sería intelección campal pero no conocimiento. El conocimiento no es sólo lo que concebimos y lo que decimos sino que es también, y en primera línea, lo que queremos decir. El lenguaje mismo no es, para los efectos de la intelección, algo meramente representativo"[170]

A la matemática se le atribuye frecuentemente un sistema conceptual y lingüístico excesivamente rígido. Pero el dogmatismo conceptual y lingüístico obstaculiza la creación matemática (y de cualquier tipo). Es necesario la flexibilidad para que conduzca a la gran riqueza creativa de la matemática.

"Lo he subrayado siempre muy enérgicamente: es menester la reconquista de la exactitud y de la precisión en los conceptos y en las expresiones. Pero esto no significa ni remotamente que esta analítica de la función lógica, precisa y exacta, sea la estructura del conocimiento. Porque el mundo no tiene una estructura lógica sino una respectividad real. Y sólo por esto es el conocimiento lo que es: la marcha hacia el sistema de la realidad"[171]

Los conceptos y las expresiones lingüísticas, para Zubiri, tienen una evolución histórica. Camino Cañón nos ofrece un ejemplo que da razón de esta constitución histórica de los conceptos matemático frente a la postura ahistórica de Kant (también de los neopositivistas lógicos y el dogmatismo matemático): el importantísimo concepto de función [172] .Dice:

"Como veremos, el concepto de función tiene una génesis rastreable históricamente. Su configuración es fruto de un proceso laborioso en el cual el lenguaje matemático del momento juega un papel decisivo. Creación de un nuevo lenguaje o afinamiento en su uso, es requisito para el avance de la configuración conceptual. Condición necesaria, aunque como veremos no suficiente. La audacia en extender el lenguaje matemático a las descripciones de nuevas realidades físicas observadas, será el motor decisivo para la consolidación definitiva del concepto" [173]

Maurice Loi en su artículo "Rigor y ambigüedad"[174] trata también del concepto de función mostrando cómo ni históricamente ni en la actualidad ha sido un término unívoco, sino por el contrario ambiguo, y sin embargo ninguno como él es tan fecundo en la matemática. El autor alude a Russell quien nos dice en 1910: " El problema de la naturaleza de una función no es, en modo alguno, una cuestión fácil... Este tipo de ambigüedad constituye la esencia de una función", y en The Principles of Mathematics: "La variable es quizás la noción más matemática de todas las nociones de las matemáticas; y también es, por cierto, una de las más difíciles de comprender". Opinión que es compartida por Hermann Weyl: "Nadie puede decir lo que es una variable". M. Loi, tras su análisis de la riqueza y ambigüedad de la noción de función, acaba señalando que es un peligro para la matemática el prejuicio, común entre los profesores de matemáticas, de exigir que los términos o conceptos matemáticos tengan un sentido único sentido, fijado desde su creación y que siempre permanezca exactamente idéntico a sí mismo. Y lo refuerza con la convicción de Heyting: "Una lengua matemática fundamentalmente unívoca es imposible".

Lakatos ofrece algunos análisis heurísticos[175] de algunos conceptos matemáticamente importantes generados por la prueba: convergencia uniforme, variación acotada, y la definición de Carathéodory de conjunto medible. Opone su método heurístico, que muestra la "lógica" que ha dado a luz al nuevo concepto, "al estilo deductivista [que] desgaja las definiciones generadas por la prueba de sus "pruebas-antepasadas" y las presenta aisladamente de un modo artificial y autoritario. Oculta los contraejemplos globales que han llevado a su descubrimiento"[176] Sin algún tipo de continuidad los conceptos nuevos aparecen como algo puramente gratuito, inmotivado, irracional, producido por generación espontánea, de la nada. Dice Lakatos:

"El análisis de la prueba de Dirichlet estaba equivocado tan sólo por lo que respecta a la tercera condición: de hecho la prueba descansa tan sólo sobre la variación acotada de la función. Se criticó el análisis de la prueba de Dirichlet y su error lo corrigió C. Jordan en 1881, quien se convirtió en el descubridor del concepto de variación acotada. Sin embargo, no fue él quien inventó el concepto, no due él quien lo "introdujo", sino que más bien lo descubrió en la prueba de Dirichlet en el transcurso de un reexamen crítico" [177]

Y en una nota a pie en la palabra "introdujo", dice:

"¡La ‘introducción’ de un concepto a partir de la nada es una operación mágica a la que se recurre muy a menudo en la historia escrita al estilo deductivista!" [178]

Pues bien, igual que Lakatos, Zubiri considera que no hay generación espontánea en ninguna creación de conceptos. Si el pasado no nos hubiera legado sus insuficientes posibilidades, no habría manera de que las cosas acusaran su peculiaridad. Con lo cual el pasado no sólo nos otorga un estado sino una situación. Nos otorga una vía de acceso a las cosas, una ruta.

"La visión que en un momento tenemos de las cosas se halla montada, a un tiempo, positiva y negativamente, sobre la posibilidad que el pasado nos dio. El pasado está pues en el presente: el pasado no sólo produjo el presente, sino que está haciéndonos presentes. Las posibilidades con que contamos, en lo que no tienen de realidad, son puro pasado inexistente; en la medida en que positivamente posibilitan lo que somos, son lo que en nosotros hay de presente. De esta suerte el presente es también inexorablemente pasado"[179]

La Matemática se construye no sólo desde las posibilidades legadas por la tradición, sino también desde la posibilidad sentientemente presente, esto es sugerida por las realidades actualizadas en intelección sentiente. La posibilidad está sugerida por los sentires en su carácter de "hacia". Cada sugerencia es una "entre otras" y la inteligencia tiene que optar entre todas estas posibilidades co-sentidas, co-sugeridas. La sugerencia como proceso mental está determinada por el carácter sugerente de la realidad física. A partir de la sugerencia se elabora el esbozo. La razón sentiente es en última instancia razón que se mueve en tanteo, y lo que tantea es formalmente la adecuación de la verificación. La dialéctica de la adecuación es tanteo, y lo que tantea es formalmente la adecuación de la verificación. La dialéctica de la adecuación es tanteo progresivo de la verificación.

En inteligencia sentiente hay verificación de verdades de la realidad matemática, y esto es un momento esencial: el progreso. Las verificaciones no son absolutas ni en la línea de la suficiencia ni en la de excedencia, sino una marcha hacia una verificación en lontananza. Cada momento de ella es verificación provisional: parcial inadecuación. Provisional no quiere decir que no sea verdad, sino que aún siendo verdad, es una verdad que está llamada no a ser forzosamente derogada, pero sí a ser superada.

El pensar es una intelección incoada. Todo inteligir pensante, por ser incoativo, abre una vía. Todo punto de llegada es a su vez punto de partida. El carácter inquiriente de la razón imposibilita un conocimiento definitivo. El llamado "Principio de Propagación de las Cuestiones" que sugiere Recher, se debe sencillamente al carácter e la razón sentiente, que por ser tal es inquiriente y esbozante, y sólo así va inteligiendo en su marcha hacia la realidad profunda. Lo real da que pensar, los problemas se descubren en contacto con la realidad. La apertura de la realidad es absoluta, de tal modo que por mucho que encontremos nunca agotamos la inmensa riqueza de lo real. Por otra parte, dado que el término formal del conocimiento era el "podría ser", el fundamento de lo real como posibilidad libremente construida. Por tanto es de limitada fecundidad. Y al ser elegido entre otros, el sistema es de "amplitud" limitada.

"Todo conocimiento, por ser una intelección con un sistema de posibilidades libremente construido desde un sistema de referencia, es un conocimiento abierto, no sólo de hecho y por limitaciones humanas, sociales, y históricas, sino que es abierto en cuanto conocimiento por necesidad intrínseca, a saber, por ser intelección en esbozo. Y esto es un momento formalmente constitutivo de la intelección racional en cuanto tal"[180]

Y,

"La tarea de la razón es indefinida no sólo en el sentido de que jamás agotará lo que en concreto se propone inteligir, sino que es indefinida ante todo y sobre todo porque lo inteligido mismo, a saber lo real en cuanto real, es formal y constitutivamente abierto, y por tanto jamás clausurado" [181]

La filosofía, según Zubiri, tiene ante todo un horizonte de intelección. Señala como horizontes de la filosofía europea:

1. Filosofía griega: el movimiento.

2. A partir del cristianismo: nihilidad.

Pues bien, nosotros creemos que el nuevo horizonte filosófico de la filosofía de la matemática, en general, es la Apertura o Incompletitud. Lo hemos resaltado en Lakatos y en Zubiri. Y constatamos que es el Teorema de Gödel (1931) el que ha definido este nuevo horizonte intelectual. Aunque su origen es matemático, sus efectos han tenido repercusión en todo el conocimiento. No hay fundamentos últimos, no hay evidencias últimas, no hay sistemas formales completos. El conocimiento matemático (y en general) es abierto al infinito, no puede detenerse el regreso al infinito ni en las definiciones, ni en las teorías. Esto se debe a la insondable riqueza y profundidad de lo real matemático, y al carácter sentiente de la intelección matemática, que sólo puede conocer de forma procesual.

Con este capítulo concluimos las cuestiones capitales de la filosofía de la matemática de Zubiri: intelección racional, objeto y verdad. La red triangular trazada por el autor: Constructivismo sentiente, transcendental, y Lógico-histórico o Histórico-lógico, es un nuevo paradigma que alumbra una dirección fecunda en la orientación de los graves problemas planteados en la actual filosofía de la matemática.

 

 

CONCLUSION

 

La conclusión general de esta tesis doctoral es que existe una dependencia entre la matemática y la filosofía de Zubiri, según una doble dimensión:

1. La filosofía de Zubiri nace, en gran parte, de la necesidad de fundamentar la matemática de su tiempo y de interpretar sus resultados. La evolución del pensamiento de Zubiri es paralela al desarrollo de la matemática de su tiempo. No puede eludirse, pues, el contexto matemático-lógico en la génesis del pensamiento filosófico del autor.

2. A partir de la filosofía de Zubiri puede hallarse respuesta al problema del fundamento y de la naturaleza de la matemática. Su aportación es tan original y fecunda, que nos ha llevado a considerar a Zubiri como fundador de una nueva "escuela" de filosofía de la matemática: un Constructivismo Sentiente, Transcendental y Lógico-histórico.

Presentamos nuestros resultados, de modo más concreto, según el orden establecido en los distintos capítulos.

CAPITULO I.

1. La matemática, para Zubiri, es un campo privilegiado de sugerencia filosófica. La interpretación de los resultados de la matemática de finales del s. XIX y principios del s. XX (hasta 1930 aproximadamente) — de modo especial: las geometrías no euclídeas y la matemática transfinita de Cantor — llevan a Zubiri a una Filosofía de la Objetividad, continuadora de la Fenomenología de Husserl. Es su primera etapa en filosofía de la matemática (y de su pensamiento en general).

2. Zubiri considera en su filosofía objetivista-ideal de la matemática que ésta se ocupa de objetos ideales, parte de eviden-cias apodícticas y su método es deductivo "a priori". Su concepción está en continuidad con la de Platón, Husserl y Hilbert.

3. El teorema de Gödel (1931) es un factor decisivo en el giro filosófico que se opera en Zubiri del objetivismo al realismo en la filosofía de la matemática y en su pensamiento en general. Así como de la interpretación objetiva-ideal de la matemática pre-gödeliana nace una Filosofía de la Objetividad, de la interpretación realista de la matemática post-gödeliana nace, en gran parte, una Filosofía de la Realidad. La revolución filosófica de Zubiri está en concordancia con la revolución matemática de Gödel.

4. El concepto de función matemática es "clave de bóveda" de la actual matemática. Russell y Zubiri (posiblemente influido por el primero) han sido quienes han dado a esta noción un rango filosófico eminente. Supone un cambio paradigmático en la concepción del objeto de la ciencia y de la filosofía, de la visión de la realidad y de su descripción. La noción de causa queda desplazada por la de función; la descripción predicativa de la realidad por la descripción funcional; y el sujeto sustancial (que está en la base de la noción de causa) por la estructura funcional (sustantividad).

CAPITULO II.

1. La "noología" de Zubiri es un supuesto de su epistemología matemática. La radicalidad del planteamiento del autor, frente a la generalidad de los estudios de filosofía de la matemática, estriba en el análisis previo de la intelección. Toda la tradición filosófica ha partido de la dualidad entre sentir e inteligir porque se ha lanzado por la vía del contenido de la realidad. Esto es, según Zubiri, fuente de dos errores: la logificación de la inteligencia y la entificación de la realidad. Él parte, por el contrario, de la inteligencia sentiente y la vía de la formalidad de realidad, que le lleva a la inteligización del logos y la reificación del ente. Este giro "noológico" tiene una gran repercusión en la filosofía de la matemática.

2. La filosofía matemática constituye una piedra angular de la Trilogía sobre la intelección de Zubiri. Tanto es así que puede reconstruirse su noología desde una filosofía de la matemática. Las nuevas nociones de inteligencia, de realidad y de verdad, expuestas en este conjunto de obras, son los ejes del constructivismo sentiente, transcendental y lógico-histórico.

CAPITULO III

1. La fuerza de la Filosofía Sentiente de la Matemática de Zubiri consiste en la utilización del método fenomenológico para su elaboración. Es un hecho que la inteligencia concipiente se funda en la inteligencia sentiente y, paralelamente, la filosofía concipiente de la matemática se funda en la filosofía sentiente de la matemática. El constructivismo de Zubiri es una filosofía sentiente de la matemática, frente a otros tipos de constructivismos y de concepciones que son filosofías concipientes de la matemática. De ahí que la filosofía de la matemática zubiriana pueda fundamentar y vertebrar el resto.

2. Zubiri sigue la línea constructivista kantiana de la matemática, sin embargo, su constructivismo no es sensible (como el de Kant), sino sentiente. Esta diferencia es fundamental.

3. En clara oposición a toda la tradición racionalista, logicista y formalista de la matemática, Zubiri sostiene, desde la inteligencia sentiente, una postura sensista de la matemática. Si no sintiéramos lo matemático, no podríamos construir la matemática. La construcción sentiente de la matemática no es conceptuación sino realización de un contenido libremente creado "según conceptos" en la impresión de realidad. Es una operación física y no mental.

4. El autor aporta un nuevo paradigma de sentir que supone una revolución en la filosofía de la matemática. El modo paradigmático de sentir no es "sentir lo sensible", sino "sentir lo real". Es toda la diferencia entre la inteligencia sensible y la inteligencia sentiente; ésta siente no sólo el contenido sino también la formalidad de realidad como "de suyo". Las cosas físicas y los objetos matemáticos se sienten de forma idéntica en su impresión de realidad, la diferencia está en el contenido de realidad. Sentimos lo matemático porque el contenido libremente construido se inscribe en la formalidad de realidad dada impresivamente. De los objetos matemáticos hay impresión, pero no sensible, sino meramente impresión transcendental.

5. El sensismo matemático de zubiri no es el sensualismo de J. S. Mill y de Feyerabend. No se trata de reducir el contenido de la matemática al contenido sentido de las impresiones sensibles, sino de la reducción de la construcción matemática a lo sentido en la línea de la formalidad de realidad campal. Es la mismidad de la impresión de la formalidad de la realidad matemática y la realidad campal.

6. El sensismo y el constructivismo se concilian desde la inteligencia sentiente, de tal modo que los objetos matemáticos son construidos sentientemente. Los conceptos matemáticos se obtiene por intelección constructiva. La inteligencia sentiente los construye en "la" realidad campal que nos dan las cosas reales concretas, pero desrrealizada del contenido particular que tengan. El juicio matemático es la realización de un concepto constructo en la realidad postulada. Los postulados matemáticos postulan el contenido de "la" realidad y no mera verdad. Las distintas geometrías son, por tanto, postulación constructiva teorética.

7. La libre construcción matemática se apoya en la constructividad de la realidad campal (no en su contenido o estructura). Y su carácter racional consiste en la unidad coherencial propia de lo creado. Esta unidad es intelectiva, y al realizarla en la impresión de realidad se transforma en unidad de lo real matemático. En este sentido, la construcción matemática y la de la literatura de ficción son semejantes; sólo difieren en que la primera es "según conceptos" y la segunda "según perceptos y fictos".

8. El método constructivo-sentiente de la matemática se opone al método lógico-formal. Es vía en la realidad postulada y no en el pensamiento. La intelección sentiente de la matemática no coincide totalmente con la intelección lógica, porque tiene además del momento de la estructura lógica, el de la actualización de lo real matemático. Frente al Positivismo Lógico, al logicismo y al formalismo, Zubiri considera, desde la inteligencia sentiente, que el método matemático no es la deducción, sino un modo de experiencia: la com-probación física.

9. La construcción conceptiva de la matemática se funda en la construcción sentiente. Las dificultades del constructivismo sensible de Kant se superan desde el constructivismo sentiente de Zubiri. La construcción conceptiva tanto del axiomatismo formalista de Gödel y Cohen como del intuicionismo de Brouwer no es suficiente para tener ciencia de realidad matemática, es necesario proyectar el contenido construido "según conceptos" en la impresión de realidad.

CAPITULO IV

1. Si en el capítulo anterior hemos defendido, desde el punto de vista de la intelección matemática, el carácter sentiente del constructivismo de Zubiri, en este capítulo hemos defendido, desde el punto de vista del objeto matemático, el carácter transcendental del mismo. Zubiri sostiene "a una" el sensismo y el transcendentalismo en la matemática. Son dos aspectos congéneres claves de su constructivismo. El transcendentalismo de la matemática consiste en afirmar que la construcción matemática sólo es posible por el momento transcendental de la física realidad campal dada impresivamente en aprehensión primordial de cualquier cosa real. De ahí nuestra denominación de Constructivismo Transcendental.

2. Zubiri propone un nuevo paradigma de la transcendentalidad que conlleva (al igual que el cambio de paradigma del sentir) una revolución de la filosofía de la matemática. Transcendentalidad es un momento de la realidad, es el "trans" que posee la formalidad de realidad campal respecto de los contenidos determinados de las cosas sentidas. No es un momento conceptivo, sino sentido y físico. La transcendentalidad de la formalidad de realidad sentida es un ámbito que hace posible que la inteligencia humana se mueva libremente y construya los distintos contenidos de los objetos matemáticos. La espaciosidad es el ámbito transcendental de realidad que posibilita en la geometría la libre construcción de los espacios geométricos. El fundamento matemático no es, pues, un principio lógico o una intuición evidente, sino el ámbito transcendental de realidad. La matemática vive de la metafísica.

3. El transcendentalismo y el constructivismo se concilian desde la inteligencia sentiente de tal modo que el objeto matemático es constructo transcendental o realidad "en construcción". Así pues, el objeto matemático es real en la misma realidad que las cosas reales "en y por sí mismas". La diferencia está meramente en su contenido, en el primer caso postulado en "la" realidad dada y en el segundo dado sensiblemente. Los objetos matemáticos, a pesar de ser realidad "en construcción", "en postulación", "en libertad", "en concepto", son estricta realidad porque tienen propiedades "de suyo", "en propio" y no sólo las postuladas o deducidas de los axiomas y postulados (Teorema de Gödel). No son cosas físicas, ni mentales; son cosas libres.

4. Los objetos matemáticos existen aunque su existencia no es "en y por sí misma" como la de esta piedra, sino postulada. Ésta consiste en la nuda realización del contenido en "la" realidad. La realidad existente del objeto matemático es idéntica a la de un personaje de una novela de ficción. Ambos son constructos transcendentales.

5. Los teoremas de Gödel y de Cohen apoyan la concepción zubiriana de la anterioridad de la realidad sobre la verdad matemática. Por otra parte, hay una cierta afinidad entre el realismo matemático de Gödel y el de Zubiri.

6. El constructivismo transcendental permite explicar el isomorfismo entre espacio geométrico y espacio físico, y, en general, entre la matemática pura y la matemática aplicada.

7. El constructivismo transcendental no es, como el resto de los constructivismos, un finitismo, sino un transfinitismo. El infinito actual ( y, por tanto, el continuo ) es un constructo transcendental o "real". Su contenido "según conceptos" se proyecta sentientemente en el ámbito transcendental de realidad. El resultado es algo "de suyo" que le impone al matemático la tarea de su comprensión.

8. El constructivismo transcendental establece, frente al logicismo de Russell, el nexo entre metafísica y lógica en la matemática. La lógica formal no sólo no es fundamento de la matemática, sino que ella misma se funda en la lógica de la intelección afirmativa de lo real. La construcción transcendental matemática es tarea exclusiva de la inteligencia humana porque sólo ella siente "la" realidad; por consiguiente, una máquina podrá realizar cálculos formales, pero al no moverse en "la" realidad no nos proporcionará nuevos conocimientos matemáticos. El teorema de indecidibilidad de la aritmética de Church pone de manifiesto la irreductibilidad del carácter sentiente de la inteligencia humana al carácter computable de un mecanismo electrónico.

CAPITULO V

1. El constructivismo matemático de Zubiri es un hito en la filosofía de la matemática. Establece un nuevo tipo de verdad, esto es, un nuevo tipo de conexión entre deducción racional y contenido de experiencia, entre creación y descubrimiento, entre lógica e historia.

2. El teorema de Gödel lleva a Zubiri a abandonar el dogmatismo de su primera filosofía de la matemática. Significa, según la interpretación zubiriana, la inadecuación de la verdad matemática a la realidad postulada. La verdad matemática es aproximación aspectual a la realidad matemática. No obstante, Zubiri, frente a Lakatos, no abandona la tarea de la fundamentación de la matemática. Su falibilismo está en la línea del contenido no en la línea de la formalidad de realidad. El regreso al infinito en el conocimiento matemático se debe a la respectividad de lo real matemático

3. El teorema de Gödel muestra que la verdad matemática no es idéntica a la demostrabilidad. La verdad matemática es verdad empírica. Dicho teorema conduce también a la disolución de la distinción entre verdades de razón (necesarias) y verdades de hecho (contingentes). Las verdades matemáticas no son verdades de razón, sino verdades de realidad postulada; y no son verdades necesarias, sino que penden de la realidad dada "en y por postulados" si éstos cambian, la verdad matemática cambia también.

4. La concepción de verdad matemática que aporta Zubiri es la Teoría de la Conformidad de la verdad matemática con lo real. La verdad real funda la verdad matemática. La verdad real de lo matemático consiste en la verdad de "la" realidad del campo o ámbito transcendental de realidad sobre la que se construye la matemática.

5. Las verdades matemáticas, según la intelección campal, son: evidentes, rigurosas, exactas y ciertas, pero no más que cualquier intelección campal. Estos caracteres se justifican desde "la" realidad aprehendida y no desde la intelección lógica.

6. Las verdades matemáticas "a una", pro indiviso, se encuentran y se descubren, y "a una", pro indiviso, son lógicas e históricas. Su carácter lógico se debe al encuentro de algo buscado, y el carácter histórico al cumplimiento de la realización de un esbozo de posibilidades. Por ser la construcción matemática lógica e histórica, denominamos al constructivismo matemático de Zubiri, Constructivismo lógico-histórico. Desde éste el carácter de evidencia, rigor, certeza, carácter necesitante y exactitud de la verdad del logos matemático se concilia con el carácter histórico de la verdad de la razón matemática. El constructivismo sentiente y transcendental de la matemática es, pues, un logicismo cumpliendo y un historicismo encontrando, esto es, un logicismo histórico y un historicismo lógico. Zubiri supera de este modo las dificultades tanto del historicismo-alógico como del logicismo-ahistórico.

 

 

 

NOTAS

[1] TFJ, p. 13^

[2] Brunschvicg, Las etapas de la filosofía de la matemática, p.498.^

[3] Brunschvicg, o.c. p. 301-2^

[4] Esta es precisamente la contribución de la reciente obra de C. Cañón: La Matemática: creación y descubrimiento (1993). ^

[5] Cf. Lakatos, "Regresión infinita y fundamentos de la matemática", (ponencia en el simposio sobre fundamentos de matemática, celebrado en la Aristotelian Society -Mind Assocciation Joint Session at the University of Leicester, Julio 1962) recogido en Matemáticas, ciencia y epistemología , (pg. 15-41), p. 16^

[6] Lakatos, Pruebas y refutaciones, p. 20.^

[7] Respecto al desarrollo de la lógica matemática son fundamentales las afirmaciones leibnizianas: las verdades de razón son necesarias, es decir, "válidas para todos los mundos posibles" y el carácter "infalible" de los "argumentos formales" (que con la aportación de Gödel y Turing se han precisado como procedimientos mecánicos o algorítmicos). Leibniz juzga del silogismo aristotélico "que garantiza la infalibilidad". Este ideal tiene entusiastas seguidores, en primer lugar Frege. La Begriffsschrift fregeana (1879) es el intento de realizar este ideal de infalibilidad sustituyendo la intuición (que puede ser errónea) por un procedimiento lógico, sin posibilidad de "huecos" en la cadena. ^

[8] Lakatos: Matemáticas, ciencia y epistemología, pp. 23-4^

[9] Lakatos, o.c., p. 173^

[10] El popperiano Watkins en su artículo "el enfoque popperiano del conocimiento científico" (recogido en la obra: Progreso y racionalidad en la ciencia,), afirma que profundidad y certeza como ideales de la ciencia son antagónicos. Desde las últimas décadas del s. XIX ha persistido, a través de muchos de los que han filosofado sobre la ciencia, el tema de la aversión hacia la profundidad, prefiriendo certeza sobre profundidad. "Parece, dice, que la primera oposición de palabra y de hecho a la opinión mayoritaria fue la de Popper (1934); el ideal de certeza fue en conjunto descartado y se favoreció la profundidad científica, el poder explicativo y una contrastabilidad exigente" . Watkins denomina a esta pretensión de certeza el ideal Bacon-Descartes. Certeza es opuesto a profundidad. Las teorías que buscan la certeza son el "fenomenalismo-verificacionismo". Este intento es inútil. Y las teorías que buscan la profundidad son las teorías "conjeturista-realista". Este intento es fructífero.

Radnitzky en su artículo "De la fundamentación de las teorías a la preferencia fundamentada de teorías" (en Progreso y racionalidad de la ciencia, p. 289), afirma igualmente que certeza y profundidad entran en conflicto y que si se atiende a uno se abandona al otro. Así la filosofía positivista busca la certeza pero atendiendo al saber superficial y la filosofía falsacionista de Popper busca la profundidad manteniendo la falibilidad.^

[11] Lakatos, o.c. p.39^

[12] Lakatos amplía el término empirista a toda teoría que tenga el valor de verdad "inyectado en la base" sea ésta espacio-temporal, aritmética o de cualquier otro tipo.^

[13] Lakatos, Matemática, ciencia y epistemología, p.17^

[14] Russell, 1901 b, pp71, cita de Lakatos, o.c. p.29^

[15] Russell, 1959, pp. 212, cita de Lakatos, o.c. 34.^

[16] Lakatos, o.c., p. 35^

[17] Ibid. p.35^

[18] Ibid, p. 37^

[19] Ibid, p. 39^

[20] Lakatos, Matemática, ciencia y epistemología, p. 24 ^

[21] Ibid, p. 41^

[22] TFJ, p.180, subrayado nuestro^

[23] TFJ, p.32^

[24] TFJ p.31^

[25] Zubiri no califica explícitamente a la Matemática de infalible, sí dice de la Fenomenología, que "Este conocimiento es absoluto e infalible" (TFJ. 47) y en cuanto que las ciencias ideales están en el mismo plano, cabe atribuir este mismo carácter a la Matemática.^

[26] Cfr. TFJ , pp.27-8^

[27] TFJ p.188.^

[28] Téngase en cuenta que por apoyarnos en este aspecto en la obra de Zubiri Sobre la Esencia la designación que da a las realidades postuladas matemáticas no es ésta, que aparece en la Trilogía de la Intelección, sino que las denomina cosas objetuales. Pero en este caso asemeja igualmente a las realidades frente a los conceptos objetivos. Objetividad y objetualidad son radicalmente distintos. Los entes matemáticos son objetos no conceptos objetivos. Y en este sentido son entidades positivas. Por ello es aplicable, como el mismo Zubiri hace notar, el análisis de la incontradicción no sólo a lo físico sino también a lo matemático.^

[29] S.E p. 66^

[30] S.E p.281-2^

[31] Kant hace también la distinción entre posibilidad lógica y posibilidad matemática, Para que se de el objeto matemático no basta con conceptos puros y su consistencia sino que es preciso también la intuición.^

[32] S.E p.67^

[33] SE p.67^

[34] SE p.67^

[35] Ibid. p.68 (subrayado nuestro)^

[36] Ibid. p.68 (subrayado nuestro)^

[37] Cf. Ibid p.70^

[38] Cf. I.R pp.281-2^

[39] TFJ p.32^

[40] TFJ p.32^

[41] IL p.324^

[42] Il p.325^

[43] IL p.120^

[44] IL p.326^

[45] IL p.326 ^

[46] IL p.327.^

[47] IL p.327-8 (el subrayado es nuestro).^

[48] IL p.321-322^

[49] IL p.324^

[50] IR p.271^

[51] IR p. 272^

[52] IR p.114^

[53] IR p.115^

[54] IR p.168^

[55] IR p.103^

[56] IR p.118^

[57] Hempel, "Sobre la naturaleza de la verdad matemática", en Matemática, Verdad, Realidad, pp.12-33^

[58] Quine, W.V. " Los fundamentos de la matemática", 1964, pg. 223, en Matemáticas en el mundo moderno, M. Kline.^

[59] Lakatos, ¿Existe un renacimiento del empirismo en la reciente filosofía de la matemática? (1967) en Matemáticas, ciencia y epistemología, cap. 2:. pp. 42-66.^

[60] Dentro del "nuevo campo falibilista" , Lakatos incluye a Russell que,en 1924, nos dice que la lógica y matemática es aceptada igual que la electrodinámica de Maxwell, por sus consecuencias observadas; a Church que, en 1939, sostiene que no podemos tener fiabilidad de la consistencia del sistema formal de Russell o Zermelo; a Gödel que, en 1944, dice que la crítica de fundamentos nos lleva al abandono de su certeza absoluta; a Carnap que, en 1958, encuentra una cierta semejanza entre la física y la matemática en cuanto a su falta de certeza absoluta.; a Quine que, en 1958, constata el carácter evaluativo de los datos empíricos también en las matemáticas; a Rosser que, en 1953, se une a Gödel en cuanto que no tenemos seguridad de que un sistema formal esté libre de contradicciones; Weyl que, en 1949, propone el parangón de la matemática con la física; Mostowski, en 1955, toma el teorema de Gödel como corroborador de la caracterización de la matemática como una ciencia natural más, con el mismo método que ésta: la experiencia; Kalmar, en 1967, afirma que la matemática tiene que ser contratada en la práctica como el resto de las ciencias.^

[61] Cf. "El método de análisis-síntesis", en Matemáticas, ciencia y epistemología, p. 130-1.^

[62] Pruebas y Refutaciones, p.166, nota 40^

[63] Ibid p.166^

[64] C. C. Cañón, (1993), p. 303, la referencia interna de Shanker, es (1987), p. 284.^

[65] Ibid, p. 400^

[66] La gran atracción que ejercen las verdades matemáticas, en gran parte, es debida a su ropaje de eternidad e inmutabilidad como el que se nos suele aparecer. Incluso, a pesar de que la conmoción interna en la matemática ha llevado a la mayoría de filósofos actuales de la matemática a abandonar el dogmatismo matemático, observamos que sigue siendo la opinión común y los propios alumnos de bachillerato suelen esgrimir este carácter de la matemática para dudar del valor de la filosofía. ^

[67] Kneale, Desarrollo de la lógica, p.603^

[68] IR p. 279^

[69] IR p.279^

[70] Ibid p.279^

[71] Ibid p.279^

[72] Hume: Investigaciones sobre el entendimiento humano,IV, en Verneaux, R. Textos de los grandes filósofos. Edad Moderna, Herder, Barcelona, l982, 107-8)^

[73] IR p.280-1^

[74] Ibid p.281^

[75] En la colección de artículos de Lakatos Matemáticas, ciencia y epistemología, es interesante para este problema de la continuidad de la necesidad física y la necesidad lógica el artículo: "Necesidad, Kneale y Popper" p. 165-173. Es una réplica de Lakatos a una comunicación de Kneale en la conferencia anual de la British Society for the Philosophy of Science, 1960. El escrito de Kneale fue publicado en 1961 con el título "Universalidad y necesidad". ^

[76] IR p 282^

[77] Ibid p.283^

[78] Ibid p.283^

[79] IR p.84^

[80] IS, p.231 subrayado nuestro.^

[81] IS p 233^

[82] IS p 234^

[83] IS p 234 ^

[84] IL p.266 ^

[85] IL p.268 ^

[86] IS p 235^

[87] IS p.235^

[88] IS p.235^

[89] IS p.242^

[90] IL p.267^

[91] IL p.269^

[92] IL p.297^

[93] IL p 301^

[94] IL pp.305-6^

[95] IL 307^

[96] IL p.292^

[97] IL p 293-4^

[98] IL p.289^

[99] IL p 310^

[100] Ver Richard Von Mises, "Los postulados matemáticos y el entendimiento humano" en Matemáticas, Verdad y Realidad.^

[101] IL p. 388^

[102] I.L p. 221^

[103] I.L p. 225^

[104] I.L p. 223^

[105] IL p. 227^

[106] IL p. 314^

[107] IL p. 311^

[108] IL p. 236^

[109] IL p. 230^

[110] IL p. 230^

[111] IL p. 231^

[112] IL p. 231^

[113] IL p. 231^

[114] IL p. 247^

[115] IL p. 247^

[116] IL p. 232^

[117] IL p. 245^

[118] IL p. 232^

[119] IL p. 232^

[120] IL p. 232^

[121] I.L p. 177^

[122] IL p. 180-1^

[123] I.L p. 192^

[124] I.L p. 193^

[125] IL p. 196^

[126] IL p. 205^

[127] Lakatos, Pruebas y Refutaciones, p. 23-5 ^

[128] No es nuestro objeto hacer una exposición de esta cuestión en la actual filosofía de la matemática. C. Cañón presenta en su obra Matemáticas: creación y descubrimiento, p. 289 y ss. un estudio de las interpretaciones del avance de la Matemática desde la perspectiva evolutiva en R.L.Wilder, desde la Kuhniana en Ph. Kitcher, y desde la popperiana y kuhniana de Lakatos. A esta perspectiva del avance opone la perspectiva del funcionalismo formal de MacLane.^

[129] C. Cañón (1993) p. 392^

[130] Ibid, p. 402^

[131] Zubiri hace un planteamiento general de la razón, por tanto no es específicamente una filosofía de la matemática sino una noología. Las cuestiones a las que alude se refieren a toda intelección racional del tipo que sea. Nuestra interpretación de que su noología es simultáneamente una filosofía de la matemática es la que justifica que concretemos y apliquemos al ámbito de la matemática lo que Zubiri formula con una extensión general. A veces lo advertimo y otras no. Cuando Zubiri explícitamente se refiere a la matemática se ve claramente por las citas aludidas, de lo contrario es nuestra aplicación. ^

[132] IR p. 292^

[133] IR p. 261^

[134] IR p. 261^

[135] IR p. 262^

[136] IR p. 74-5^

[137] IR p. 96^

[138] IR p. 262^

[139] IR p. 295^

[140] IR p. 297^

[141] IR p. 301^

[142] Lakatos, Matemáticas, ciencia y epistemología, p. 25^

[143] Y en esto señala el autor un enorme paralelismo entre el problema de la historia y el problema del movimiento. El movimiento se consideró por los presocráticos como el paso del no ser al ser. Aristóteles es quien tuvo la genial idea de considerar el movimiento como el paso de una manera de ser a otra manera de ser. La idea de realidad se modifica: hay realidades con una dimensión de no ser. Es la idea de potencia. El movimiento entró así en la ontología, como forma del ser^

[144] IR p. 302^

[145] IR p. 302^

[146] Lakatos, Pruebas y refutaciones p. 17^

[147] Karl Manheim es uno de los responsables de la constitución, como disciplina autónoma, de la Sociología del Conocimiento^

[148] C. Cañón en su obra Matemática: creación y descubrimiento, pp. 359 ss. presenta desde su propia concepción una crítica del ideal de conocimiento y del tipo de avance matemático "ahistóricos" defendidos por Manheim. Critica también la concepción del matemático y filósofo de la matemática más reciente MacLane, quien coherente con su funcionalismo formal no da relevancia al contexto socio-histórico de la matemática. La autora presenta su postura en continuidad en este punto con la de Kitcher que se traza con cinco coordenadas interactuantes: lenguaje, conjunto de proposiciones aceptadas por la comunidad matemática en un tiempo concreto, un conjunto de esquemas de razonamiento no cuestionadas, un conjunto de cuestiones consideradas importantes, y un conjunto de puntos de vista metamatemáticos. Por último analiza el modelo de avance histórico de Wilder. Ver pp. 359-382.^

[149] La fecha podría haber sido entre 1924 (art. "Historismus" en Essays on the Sociology of Knowiwge, 1952) y 1942 (art. "Nuestra situación intelectual", en Naturaleza, Historia, Dios, 1944). Cuando Zubiri dice en el texto de 1942 "olvidan que..." parece que alude a Husserl, pero perfectamente puede referirse también a la concepción expresada por Manheim en su texto de 1924.^

[150] Manheim, "Historismus" (1924) su traducción inglesa "Historicism" se halla en Essays on the Sociology of Knowledge, Routhedge Kegan Paul, London, 1952. cit. C.Cañón (1993) p. 361-2^

[151] NHD pp. 33-4^

[152] Manheim, Ideología y Utopía, Aguilar, Madrid, 2ª ed. 1966, traducción de la versión inglesa de 1936. p.348^

[153] NHD p 40-1^

[154] La autora presenta este caso como "un ejemplo paradigmático de cómo un condicionamiento de carácter epistemológico puede obstaculizar el acceso a la verdad matemática". Ver (1993, pp. 104-107. Recoge las razones que llevan a Saccheri a abandonar las hipótesis del ángulo obtuso y del ámgulo agudo, que habrían de dar lugar a las geometrías no euclídeas, como alternativas a la hipótesis del ángulo recto. Bolyai y Lobachevski, desde la hipótesis del ángulo agudo, y Rieman desde la hipótesis del ángulo obtuso.^

[155] C. Cañón, (1993) p. 369^

[156] IR p 303^

[157] C. Cañón, o.c p. 356, subrayado nuestro.^

[158] IR p 305^

[159] IR p 305-6^

[160] IR p 305^

[161] IR p 306^

[162] IR p 308^

[163] CLF. Moneda y Crédito, Madrid, 1970.^

[164] IR p 312^

[165] Nicol, Principios de la ciencia, p 88^

[166] En el Congreso Internacional de Bolonia, en 1928 Hilbert decía: "¿qué sucedería con la verdad de nuestro conocimiento y con la existencia y el progreso de la ciencia si no hubiese ninguna verdad en las matemáticas? De hecho, actualmente aparece con demasiada frecuencia en los escritos profesionales y en lecciones orales cierto escepticismo o falta de confianza acerca del conocimiento; se trata de un tipo de ocultismo que considero perjudicial" (Attil del Congreso, 1, 1929, 141= Grundlangen der geometrie, 7ª ed. 323, citado por M. Kline, pg. 1364).^

[167] Nicol afirma también en Principios de la ciencia: "Sin continuidad no hay historicidad" p. 56. En contraposición a autores como M. Foucault que afirma "Hace falta liberarse de todo un juego de nociones que están ligadas al postulado de continuidad", tales como tradición, influencia, desarrollo, teleología, evolución, mentalidad, espíritu. Hay que suspender cualquier tipo de unidad... Aparece el proyecto de una descripción pura de los hechos del discurso. (Preguntas a M. Foucault. Círculo de la Escuela Normal Superior, París).^

[168] Crf. NHD p.438 ss., Zubiri pone el ejemplo de la constitución histórica del concepto de " ser" ^

[169] NHD p 440^

[170] IR p 215^

[171] IR p 217^

[172] C. Cañón, 1993, p.167-181^

[173] C. Cañón, ibid, p 168^

[174] M. Loi, "Rigor y ambigüedad", en Pensar la matemática. pp.275-290^

[175] Lakatos, Pruebas y Refutaciones, pp 168-178^

[176] Ibid, p 168^

[177] Ibid, p 172^

[178] Ibid, p 172, n.53^

[179] NHD p 382-3^

[180] IR p 222^

[181] IR p 102.^