CAPITULO TERCERO.

 

CONSTRUCTIVISMO SENTIENTE:

LA INTELECCION MATEMATICA

 

I. FUNDAMENTALIDAD FENOMENOLOGICA DE LA FILOSOFIA SENTIENTE DE LA MATEMATICA

 

1.1 Teoría Fenomenológica de la matemática

La radicalidad de la Filosofía Sentiente de la Matemática de Zubiri consiste en la utilización del método[1] fenomenológico para la elaboración de la misma[2]. El intento de Zubiri en la Trilogía sobre la intelección no es construir una ‘teoría’ sino realizar un ‘análisis descriptivo’. Se trata del "análisis de los hechos de intelección",

"...desde las primeras páginas del libro he advertido repetidas veces que quiero atenerme a los hechos, por ejemplo al hecho de que aprehendemos sentientemente lo real."[3]

Hoy los filósofos de la ciencia y de la matemática se cuestionan, por ejemplo, si hay o no hay racionalidad y progreso en la ciencia, si ésta refleja o no la realidad, si es representación o creación... cuestiones que se tratan sin atenerse a los hechos mismos, a la pura descripción. Zubiri acomete, como exigencia previa a toda explicación, la pura descripción de los hechos. Así vemos en su filosofía de la matemática, el realismo, la racionalidad, la creación, el progreso, etc., como hechos antes que como teorías, y son hechos precisamente de Inteligencia Sentiente. Esta es la fuerza de la perspectiva zubiriana en la filosofía matemática.

"La Fenomenología representa, pues, un terreno neutral, anterior e independiente de todas las luchas que existen en el mundo de las explicaciones".[4]

Zubiri nos proporciona una base fenomenológica de la matemática. El dato fenomenológico básico que constata es que la inteligencia es sentiente, y como corolario suyo se sigue que la inteligencia sentiente es fundamento de la inteligencia concipiente. Aplicando esto mismo al campo de la filosofía de la matemática se deducirá: La fundamentalidad de la filosofía sentiente de la matemática, y su corolario: la filosofía concipiente de la matemática se fundamenta en la filosofía sentiente de la matemática.

Nuestro planteamiento responde, pues, a la aplicación del análisis fenomenológico que hace Zubiri de la intelección al ámbito de la filosofía de la matemática, tema que nos ocupa. Y esta aplicación está totalmente justificada porque la matemática es un modo de intelección racional o de razón sentiente (como lo son también el resto de las ciencias, la literatura, la teología, etc.).

Base fenomenológica de la intelección	y		su aplicación a la filosofía matemática
1. La inteligencia es radicalmente sentiente		1. La filosofía de la matemática es radicalmente sentiente
2. La inteligencia concipiente se funda en la inteligencia sentiente.		2. La filosofía concipiente de la matemática se funda en la filosofía sentiente de la matemática.

 

La inteligencia no es concipiente ni intuitiva sino sentiente. Esto es un hecho, que nos arroja el mero análisis fenomenológico de la intelección, y, sin embargo, no ha sido visto así en toda la tradición filosófica europea. Según Zubiri: "los griegos y con ellos la filosofía europea, no ha conceptuado que la inteligencia sea sentiente" [5]. Este punto de partida, como ya hemos advertido, tiene unas consecuencias inmediatas en la filosofía de la matemática. Desde la inteligencia sensible o concipiente, el objeto de la matemática se ha considerado como un concepto o sistema de conceptos y como intuición. Ahora bien, ni una cosa ni otra son radicalmente suficientes. Habrá algo más básico que será lo dado sentientemente, como veremos.

La oposición entre sentir e inteligir, establecida por la filosofía clásica, al atender solamente la vía del contenido de la realidad y "resbalar" sobre la línea de la formalidad de la realidad, tiene una repercusión gravísima en la concepción de la matemática. Es la raíz de las concepciones logicista, formalista e intuicionista de la matemática. Pero la propia matemática se encarga de mostrar su inadecuación a esos moldes (Teorema de Gödel).

La unidad entre sentir e inteligir, según Zubiri, es estructural: la inteligencia es sentiente. El acto de inteligencia sentiente es único: impresión de realidad; en cuanto sentiente es "impresión" y en cuanto inteligencia es "formalidad de realidad". Por tanto la matemática tendrá que tener un momento sentido, esto es, tendrá que ser un modo de impresión de realidad. Recordemos que por el modo estructuralmente más elemental de la intelección, la aprehensión primordial, se nos da impresivamente un contenido en formalidad de realidad. Sentimos no sólo lo sensible sino también la realidad. En esta realidad, dada impresivamente, nos movemos tanto en el logos como en la razón, que, por esto, son igualmente sentientes[6].

A lo largo de la filosofía se ha calificado a la razón como razón pura, razón vital, razón histórica. Zubiri abarca estas denominaciones en una nueva determinación: razón sentiente. Esta nueva vía es de gran fecundidad para la matemática. La razón es una modalización de la inteligencia sentiente y por tanto sólo desde ésta se puede comprender su carácter sentiente y su acto propio. La intelección racional o conocimiento es modo de actualidad de lo real. La razón se apoya en la aprehensión primordial y en todas las intelecciones afirmativas que el logos ha inteligido sentientemente. No es razonamiento sino marcha desde lo real campal a la realidad profunda, desde la cosa real hacia la pura y simple realidad.

En la filosofía clásica se ha fundado la intelección en la inteligencia concipiente, esto es lo que Zubiri denomina "logificación de la intelección" . Esto mismo ha sucedido en la matemática pre-gödeliana, al pretender reducir —el programa logicista y en parte el formalista— la matemática a la lógica, esto es, la "logificación de la matemática" . Lo que hay que hacer es "inteligizar el logos"; dado que "la inteligencia concipiente, dice Zubiri, está constitutivamente fundada en la inteligencia sentiente"[7]. Y por lo mismo: inteligizar la matemática.

Es muy importante tener en cuenta, en toda consideración de la inteligencia, la vía que se emprende. En inteligencia sentiente esta vía es la de la formalidad de realidad y la vía de la actualidad de la realidad en la inteligencia; frente a la vía de inteligencia concipiente, que es la vía del contenido de realidad y la vía de la actividad de las cosas reales en la inteligencia. Según Zubiri: "La filosofía se ha fijado solamente sobre el contenido, pero ha resbalado sobre la formalidad"[8] . La formalidad es un momento sentido de carácter descriptivo. La formalidad de realidad o reidad supone una alteridad que pertenece a la cosa "de suyo" como modo de quedar en la aprehensión. Es la habitud del ser humano, que por ello es definido como animal de realidades. Es primaria la unidad de la formalidad de realidad al contenido de los distintos sentidos; y aunque el contenido varíe la formalidad de realidad es idéntica.

El conocimiento, en general, y el conocimiento matemático, en particular, no es juicio ni es sistema de juicios, sino que es formalmente un modo de actualidad de lo real en la intelección. Conceptualizarlo como sistema de juicios fue el gran error de toda la filosofía moderna, y sobre todo de Kant[9]. Actualidad es un estar presente desde sí mismo, desde su propia realidad. Por esto la actualidad pertenece a la realidad misma de lo actual, pero no le añade, ni le quita, ni modifica ninguna de sus notas reales. La intelección humana es formalmente mera actualización de lo real en la inteligencia sentiente[10]. Esto aplicado a la matemática, nos ofrece una concepción sentiente y no concipiente. La matemática es una actualización de un tipo de realidad, ya se verá, en la razón sentiente.

La base fenomenológica de la intelección es la base fenomenológica de la matemática, según la filosofía de Zubiri, que nos interesa destacar.

 

1.2.Fundamentalidad de la Filosofía sentiente de la matemática.

La afirmación clave en todo el pensamiento de Zubiri, como acabamos de ver, es que la Inteligencia es Sentiente, y, por tanto, que la inteligencia concipiente se funda en inteligencia sentiente. Este punto de partida es fundamental para la filosofía de la matemática, de ahí que nuestra propuesta es "Filosofía Sentiente de la Matemática", contraponiéndose a lo hecho hasta Zubiri, que podríamos interpretar, —prolongando el pensamiento de Zubiri en esta línea— como "Filosofía Concipiente de la Matemática".

El hilo fundamental de nuestra aportación es la fundamentalidad de la filosofía sentiente de la matemática frente a la filosofía concipiente de la matemática. Zubiri, en lo que nos ocupa, se ha hecho cuestión de la matemática y su tratamiento filosófico se apoya en el concepto radical de inteligencia, esto es, la inteligencia sentiente.

"La inteligencia es estructural y formalmente inteligencia sentiente este es concepto radical de inteligencia en el que hay que apoyarse para toda consideración filosófica" [11]

Es fácil inferir que, por su punto de arranque, la filosofía zubiriana de la matemática nace con la pretensión de radicalidad frente a otras concepciones. Veremos hasta qué punto es así.

 

1.2.1 Corolario: La filosofía concipiente de la matemática se funda en la filosofía sentiente de la matemática.

Paralelamente al esquema que hemos expuesto en la noología de Zubiri, contraponemos a continuación los puntos más importantes de la filosofía concipiente y de la filosofía sentiente para constatar la fundamentalidad de la filosofía sentiente de la matemática. Ahora presentamos un esbozo que iremos posteriormente desarrollando.

Filosofía concipiente de la Matemática	Filosofía sentiente de la matemática
1. Vías: a) Se ha fijado en el contenido b) Actividad: c) Representación de la realidad.	1.Vías: a) Se ha fijado en el contenido en formalidad de realidad b) Actualización c) Instalación en la realidad
2. Sus conceptos son de inteligencia concipiente	2. Sus conceptos son de inteligencia sentiente. Conceptuar es solamente un despliegue intelectivo de la impresión de realidad .
3. La matemática es una construcción concipiente	3. La matemática es una construcción sentiente: intelección "en" el sentir.
4. El objeto de la matemática: son los referentes objetivos de determinados conceptos o intuiciones.	4. El objeto de la matemática: algunos aspectos de la realidad. Realismo transcendental
5. La Matemática es un sistema de juicios o proposiciones.	5. La matemática es "aprehensión" sentiente de la realidad matemática.
6. La matemática es un lenguaje simbólico, una manera de hablar o un sistema de conceptos.	6. La Matemática es un modo de instalarnos en la realidad.
7 El método matemático: vía en la verdad.	7. Método matemático: vía en la realidad.
8. Dislocación de los momentos de la impresión, originando distintas escuelas[12]: a) sólo como contenido o afección: representación mía de lo real. E. psicologista y empirista de la matemática b) se prescinde de la fuerza de imposición: juicio. E. Logicista y formal de la Matemática c) sólo la formalidad o alteridad: E. intuicionista de la matemática. Las distintas escuelas se oponen.	8. Unidad estructural de los tres momentos de impresión de realidad: a) afección: contenido. b) alteridad: formalidad c) fuerza de imposición. En base a esta unidad estructural, las distintas escuelas de filosofía de la matemática están vinculadas estructuralmente. No hay oposición entre el intuicionismo y el axiomatismo formalista. Del mismo modo como sentidos e inteligencia forman una unidad estructural.

 

 

Hacer filosofía sentiente de la matemática es, desde luego, conceptuar, ahora bien, todos y cada uno de los conceptos tienen que ser "un despliegue intelectivo de la impresión de realidad",

"Son necesarios los conceptos, pero han de ser conceptos de inteligencia sentiente y no conceptos de inteligencia concipiente"[13]

Nos tenemos que situar desde la inteligencia sentiente para elaborar los conceptos de la Filosofía de la Matemática —la inteligencia sentiente es el fundamento de la matemática y no la inteligencia concipiente—. Hay que operar la conversión de su concepción concipiente a su concepción sentiente, como diría Kuhn, y cambiar de paradigma en la concepción de la matemática. El resultado será una Filosofía sentiente de la matemática.

En el próximo capítulo veremos que, según Zubiri, la matemática es una construcción de Inteligencia Sentiente. Esta afirmación define una postura original, no respecto a la construcción, que se admite comúnmente en la filosofía actual de la matemática, sino que la novedad está en la articulación zubiriana de "construcción" y "sentiente". La inteligencia sentiente es la que lleva a cabo la construcción matemática. Y, claro está, el modo de hacerlo será sintiendo, no conceptualizando sino realizando el contenido de unos conceptos en "la" realidad sentida en la aprehensión primordial de realidad.

Por consiguiente, lo que hemos venido denominando Filosofía Sentiente de la Matemática, para contraponerla a la Filosofía Concipiente de la Matemática, (en claro paralelismo con la oposición entre inteligencia sentiente e inteligencia concipiente, hecha por Zubiri), podemos concretarla con la siguiente denominación: Constructivismo sentiente. Nos interesa insistir en que el constructivismo de Zubiri es una filosofía sentiente de la matemática, frente a otros tipos de constructivismos de la matemática que son filosofías concipientes de la matemática.

Antes de tratar la fundamentalidad del constructivismo sentiente de la matemática frente a otros constructivismos, tenemos que hacernos la inevitable pregunta a la que nos lleva todo lo original: ¿qué es el constructivismo sentiente? . En primer lugar nos fijaremos en la línea de la formalidad de realidad para establecer el sensismo de la matemática; y en segundo lugar lo haremos en la línea del contenido para determinar la libre construcción de la matemática. Es muy importante tener en cuenta las dos líneas distintas, dentro de una única realidad, para conciliar el carácter sentiente (momento impuesto y dado) de la matemática y el carácter constructivo (momento libre y creado) de la misma. Así pues, veremos que la matemática es una construcción libre del contenido fundamental de la realidad dada en profundidad (recordemos que la profundidad es el ámbito de toda intelección racional). No basta con sentir lo matemático para tener la matemática, es preciso construirla. Pero no una mera construcción mental y arbitraria porque nos impediría el acceso a la realidad matemática, sino una construcción en la realidad sentida en aprehensión primordial.

Nuestro objetivo será mostrar cómo el carácter sentiente de lo matemático posibilita:

 

1. Intelección constructiva de conceptos matemáticos.

2. Postulación constructiva de objetos matemáticos.

3. Método constructivo de la matemática.

 

El resultado de la construcción de conceptos, de los objetos matemáticos y del método constructivo nos ofrecerá una concepción sentiente de la matemática opuesta a la concepción lógica de la misma. Y en esto Zubiri se suma a la pretensión del constructivismo kantiano, y en general de todos los constructivismos; sin embargo, no lo hace recurriendo a los sentidos o a la intuición sino a la impresión de realidad que es el acto de inteligencia sentiente. Los conceptos constructos no son meramente lógicos sino que tienen su momento de realidad sentida; los objetos construidos de la matemática no son meros conceptos o sistemas de conceptos sino que son realidad postulada; las afirmaciones constructivas matemáticas no son meros juicios lógicos sino realizaciones en la realidad postulada; el método constructivo matemático no es mero razonamiento lógico sino "dis-currir" en la realidad matemática.

 

2. ¿QUÉ ES EL CONSTRUCTIVISMO SENTIENTE DE LA MATEMATICA?

 

2.1 Zubiri: fundador del constructivismo sentiente de la matemática.

Hasta ahora hemos desarrollado, sobre todo, la primera dimensión de nuestra tesis en la que constatamos que Zubiri acude a la matemática (no de forma exclusiva, pero sí con cierta prioridad) para obtener sugerencias filosóficas sobre qué hay que entender por inteligencia y por realidad. Su aportación clave al respecto, como ya hemos visto en su "noología", es que la inteligencia es sentiente y la realidad es formalidad del "de suyo". En este capítulo se hace patente la segunda dimensión de nuestra tesis: de la filosofía de Zubiri nace una nueva "escuela" de filosofía de la matemática: el constructivismo sentiente. Exponemos, a continuación, las razones que nos han inducido a esta denominación.

En primer lugar, encontramos que Zubiri nos dice que el objeto matemático no es un concepto ni es una intuición sino una construcción. En palabras suyas:

"Todo lo matemático es construido"[14]

En este sentido, Zubiri seguiría la línea de la filosofía de la matemática denominada: constructivismo [15] matemático, cuya paternidad se atribuye a Kant. Éste sostiene que el conocimiento de la matemática se obtiene por la construcción de los conceptos, que consiste en la presentación de la intuición a priori correspondiente.[16] Como indica Javier de Lorenzo:

"...a Kant se le puede considerar como iniciador de una línea en la Filosofía de la Matemática: la calificable de constructivista. Línea que, a primeros de este siglo, adoptan matemáticos como Poincaré, la escuela semiintuicionista francesa o, más radical, Brouwer con el intuicionismo"[17]

La originalidad de Zubiri no está, pues, en iniciar la vía constructivista de la matemática, sino que, a nuestro modo de ver, está en definir un tipo determinado de constructivismo matemático, que es muy distinto del kantiano y de otros[18] Y no puede ser de otro modo, ya que para Zubiri, a diferencia de la concepción de Kant, la construcción matemática no es acto de inteligencia sensible o intuitiva, sino que es acto de inteligencia sentiente:

"La construcción matemática es siempre por tanto un acto de inteligencia sentiente"[19] .

De este modo, precisando la afirmación de Javier de Lorenzo, podemos decir que Kant no es fundador del constructivismo matemático, en general, sino de un tipo de constructivismo que, por partir de la perspectiva de inteligencia sensible o concipiente, bien puede denominarse: constructivismo sensible o concipiente. Esta aclaración nos permite afirmar que Zubiri es fundador de otro tipo de constructivismo matemático que, por partir de la perspectiva de inteligencia sentiente, podemos denominar: constructivismo sentiente de la matemática. La intelección constructiva en Zubiri es siempre sentiente [20]. Este carácter la presenta de modo muy distinto a como lo hacen otros constructivismos. Lo común a todos ellos está en que, en sentido amplio, el constructivismo matemático y metamatemático se caracteriza por su oposición al logicismo, de ahí la necesidad de recurrir a métodos constructivos en la matemática. Este rasgo está muy claro en Zubiri como lo está en Kant, Poincaré o los intuicionistas. Hay que hacer, no obstante, la observación de que actualmente incluso los logicistas estrictos recurren, de algún modo, a métodos constructivos. Como señala Javier de Lorenzo:

"prácticamente casi todas las formulaciones realizadas tras la aparición de las antinomias recurren, de una manera más o menos explícita, al constructivismo; incluso aquellos realistas platónicos que sostenían el logicismo primitivo a ultranza, tras las restricciones a sus excesos platónicos producidas por las limitaciones formalistas... han aceptado métodos que califican de ‘constructivos’"[21].

Esta nueva línea de filosofía de la matemática iniciada por Zubiri, el constructivismo sentiente, tiene en gran parte su origen, como ya señalamos, en la crisis de fundamentos provocada por el Teorema de Gödel; y, a la vez, ofrece un buen soporte filosófico para interprertarlo.

 

2.2. Construcción matemática: acto de inteligencia sentiente.

Entender qué es la matemática como construcción sentiente, nos exige precisar los dos términos que aparecen mencionados: sentir y construir; porque construcción y realidad sentida se nos han presentado como términos irreconciliables. Y esto es así, efectivamente, desde la inteligencia concipiente o inteligencia sensible, que atendiendo solamente a la línea del contenido de la intelección, considera que la construcción es "conceptiva"’ , esto es, que construir es conceptualizar lo dado por los sentidos. Y, claro, si el contenido de la matemática es construido y, por tanto, de índole no-sensible, ¿cómo puede ser sentido? Esta concepción sensible o conceptiva de la inteligencia nos deja, pues, en la dualidad: o los contenidos de la matemática son mera idealización de lo dado sensiblemente y son representación de la realidad cósmica ( no creación), o por el contrario, no nos son dados por la experiencia y son mera construcción de conceptos objetivos ( y por tanto independiente de la realidad). La primera concepción entra en crisis por los resultados de la matemática de finales del s. XIX (fundamentalmente por el descubrimiento de las geometrías no euclidianas) y la segunda concepción entra en crisis, de modo decisivo, por los resultados de Gödel. La nueva vía que ensaya Zubiri permite unificar realidad sentida y construcción, en cuanto que la inteligencia sentiente construye sentientemente.

Dada la importancia de la cuestión, precisemos a continuación la distinción entre construcción "concipiente" o "sensible" y construcción "sentiente". Mientras que construir, en inteligencia concipiente, es conceptualizar; construir, en inteligencia sentiente, no es en modo alguno conceptualizar, ni llevar a cabo cualquier operación mental ( deducir, sintetizar...), es algo muy distinto: construir es realizar, realizar "según conceptos" el contenido del objeto matemático en "la" formalidad de realidad dada en la aprehensión primordial de realidad de cualquier cosa determinada, una vez liberada de su contenido concreto. Por tanto, la construcción sentiente de la matemática es un modo de realización. Construir y realizar no son equivalentes, porque de hecho se puede realizar sin construir, ahora bien, nos dice Zubiri, "Lo que no se puede es construir sin realizar".[22] La vía de la construcción no es conceptuación sino realización. El resultado de esta operación no es un concepto sino realidad "en construcción". Se construye el contenido del objeto matemático pero en la formalidad de realidad que nos es dada por el acto de aprehensión primordial de realidad. Es una operación sentiente, esto es, de carácter físico (nos movemos en la realidad física) y no mental.

"Su construcción [de un espacio geométrico o de un número irracional] misma no es mera conceptuación sino realización, es decir algo llevado a cabo sentientemente" [23]

La base de la diferenciación entre constructivismo concipiente y constructivismo sentiente es la importantísima distinción entre conceptualización y realización. Cada modo de operación nos conduce a un tipo de resultado.

Esquemáticamente:

Tipo de construcción	operación	resultado.
*construcción "conceptiva".	* conceptualizar (Gödel-Cohen) *ejecutar operaciones en los contenidos objetivos de los conceptos. (Brouwer)	*contenidos objetivos de conceptos. *concepto objetivo de realidad.
*construcción "sentiente"	* realizar: proyectar el contenido objetivo en "la" realidad física dada en aprehensión primordial. (Zubiri)	*realidad postulada. realidad en concepto

 

Este término de realización es capital en la concepción zubiriana de la matemática (y en general). Y, como prácticamente todos los términos que introduce Zubiri en su filosofía, en principio, no está exento de dudas; porque ¿cómo hay que entender la realización ?, ¿se trata de un acto omnímodo de la inteligencia?. Si esto fuera así estaríamos ante un idealismo absoluto (el de Hegel), según el cual la realización de la Idea originaría la realidad. Nada más lejos del pensamiento de Zubiri, ya que rechaza continuamente el idealismo y racionalismo. Realizar, en nuestro autor, nunca es dar realidad. Pensarlo así sería pura vanidad pues el acto de dar realidad no es lo propio de una inteligencia sentiente. Todo lo contrario, la inteligencia sentiente recibe siempre la realidad. Ésta es un dato para la inteligencia y en ella se mueve ineludiblemente.

En otro contexto, aunque no alejado del tema, Zubiri dice que "realidad es donación" [24] . La realidad física nos es donada, de ahí que nuestro acceso a ella es a través del sentir. ¿Cuál es nuestra respuesta a esta donación? La donación (recibir desde el punto de vista del sujeto) es un momento dialéctico que por sí mismo reclama una entrega (poner algo concebido por el sujeto, pero, según sugiere el término entregar frente a dar, lo que se pone ‘su-pone’ que esto ya ha sido, de algún modo, recibido). Existe pues una estructura dialéctica entre Donación- Entrega[25], y desde ella, podríamos entender qué es realización.

En efecto, en el campo de la matemática, sería impensable la posibilidad de realizar los conceptos matemáticos si previamente la realidad no nos estuviese dada en inteligencia sentiente, y se actualizase en los contenidos de los conceptos libremente creados. Hay que vincular indisolublemente el momento receptivo (recibir realidad física) y el momento activo de la inteligencia sentiente (poner contenido creado) en la operación de realizar. Realizar es, a una, la actualización de "la" realidad (liberada de un contenido determinado) en los conceptos creados, y la realización del contenido según conceptos en "la" realidad física dada en impresión. Este acto, repetimos, no es crear realidad sino entregar mis ideas a la realidad.

"...crear no es dar realidad a mis ideas, sino que es justamente lo contrario: es dar mis ideas a la realidad. De aquí toda la gravedad de esta intelección: está en juego la física realidad misma según su contenido, es decir está en juego lo que las cosas reales son en realidad"[26]

La construcción de la inteligencia sentiente no es autónoma respecto del sentir, y, por tanto, lo concebido por la inteligencia no es independiente de la realidad sentida. Así pues, las condiciones que hacen posible la construcción sentiente de la matemática son:

 

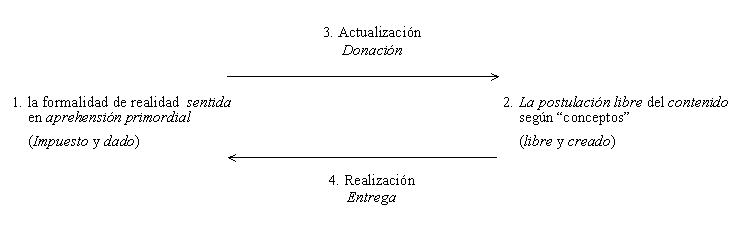
Para que se comprenda bien el constructivismo sentiente de la matemática a continuación examinaremos los siguientes puntos en Zubiri:

1. El primero nos lleva a definir su postura como "sensismo" matemático (sentir lo matemático). Es el momento de recibir impresivamente la donación de "realidad".

2. El segundo como constructivismo matemático ( libre creación del contenido del objeto matemático). Es el momento de concebir un contenido objetivo de los conceptos.

3. El tercero es la unidad de estos dos momentos a través del acto de la actualización de la formalidad de realidad en el contenido libremente creado y de la realización o de proyección del contenido creado en la formalidad de realidad dada. El primer y segundo momentos no son suficientes para proporcionarnos el objeto matemático; sólo este tercer momento es el que nos posibilita la construcción sentiente de la matemática. Pero, a su vez, esta operación supone el sentir la formalidad de realidad y la creación "según conceptos" del contenido de la realidad. Es el momento de entrega de lo concebido por mí a la realidad donada (en actualización).

 

2.3 Sensismo de la Matemática

En clara oposición a toda la tradición racionalista, logicista y formalista de la matemática (como cualquier constructivismo), Zubiri sostiene una postura sensista de la matemática (no se confunda con intuicionista). Sólo sintiendo, en primer lugar, lo matemático podemos construir la matemática. Explícitamente, nos dice:

"Sin sentir lo matemático, no se puede construir la matemática"[27]

Ahora bien, ¿Qué entiende aquí Zubiri por sentir lo matemático ? Esta es una cuestión de un alcance tal en la epistemología de la matemática, que necesariamente la respuesta va a repercutir en todas las nociones de la filosofía de la matemática, y, en términos de Kuhn, hay que esperar que un nuevo paradigma de qué sea sentir suponga una revolución en la filosofía de la matemática. Esto es, en efecto, lo que acontece en la filosofía zubiriana: su nuevo paradigma de sentir abre una nueva concepción filosófica, que no es sensible sino sentiente: el constructivismo sentiente.

El paradigma de sentir que nos ofrece la tradición filosófica es el modo de sentir las cualidades sensibles. Y ha conformado nuestras mentes de tal forma que sólo entendemos el modo de sentir este color verde, esta melodía, esta temperatura cálida, este rayo de luz, este dolor físico... Si con este paradigma de lo que se toma como sentir, nos trasladamos al campo de lo matemático y nos preguntamos ¿cómo se siente un número transfinito?, es muy probable que reproduzcamos la experiencia empirista de Hume consistente en pasar revista a todos y cada uno de los tipos de impresiones hasta hallar alguna de la cual proceda nuestra idea. Si la experiencia es negativa, en tal caso la idea no es legítima. Este es el caso en la matemática, después de examinar los once sentidos, que señala Zubiri, cuestionándonos, ¿es un color?, ¿es un sonido?, ¿es un sabor?... La respuesta siempre es la misma: No. Quedamos desconcertados, ¿cómo puede decir Zubiri que el objeto matemático, en nuestro caso el número transfinito, se siente y, sin embargo, vemos que no tiene nada que ver con las cualidades sentidas por ninguno de los once sentidos?, además ¿cómo se puede decir que se siente lo matemático si su contenido no es sensible?

Esta experiencia intelectual nos muestra que el paradigma de sentir las cualidades sensibles que llevamos para sentir los objetos matemáticos, se estrella, pues no son sensibles... y nos sale al encuentro el dilema: o los objetos matemáticos no se sienten o es preciso cambiar de paradigma de qué es sentir a fin de que en lo matemático podamos decir que se siente, porque ¿cómo se va a sentir lo matemático, por ejemplo este número irracional, inteligido por el logos, como se siente el color verde? Está claro que hay una diferencia fundamental: mientras el verde es una cualidad, el número irracional no es cualidad de ningún tipo. La tradición racionalista, logicista, formalista e incluso el empirismo de Hume optan por el primer disyunto: lo matemático no se siente, sino que es un sistema de conceptos o relación de ideas. Ahora bien, pensará Zubiri, ¿dónde está escrito que sólo se pueda sentir la cualidad sensible?

Sólo desde la perspectiva de la inteligencia sensible se ha identificado lo sentido con cualidad sensible o, en términos más estrictos, la impresión con el mero contenido sensible, y sólo desde esta perspectiva puede negarse no ya que el número irracional se sienta como el verde sino que se pueda sentir de algún modo. El objeto del sentir, desde inteligencia sensible, es lo puramente sensible, lo cual arroja un veredicto sensualista sobre los objetos: si el objeto es sensible se siente (o nos impresiona) y si el objeto no es sensible no se siente (o no nos impresiona). Los objetos matemáticos, al no ser sensibles, no se sienten. Pero, seguirá pensando Zubiri, ¿dónde está escrito que la inteligencia sea sensible o concipiente y que el sentir sea puro sentir? Este es el error de toda la tradición filosófica. Queda por ver cómo se plantea esta cuestión desde la perspectiva zubiriana de inteligencia sentiente.

La distinción entre inteligencia sensible e inteligencia sentiente es la que nos permite operar la conversión del paradigma de sentir lo sensible (desde inteligencia sensible) al paradigma de sentir la realidad física, sensible o no sensible (desde inteligencia sentiente). La tradición filosófica europea ha conceptualizado la inteligencia como inteligencia sensible pero no como inteligencia sentiente, y ha conducido a un planteamiento totalmente desviado de la naturaleza del sentir, consecuentemente, del objeto matemático. Transcribimos a continuación un texto de Zubiri que nos parece de gran claridad para justificar cuanto llevamos dicho y lo que se verá a continuación.

"Sin sentir lo matemático, no se puede construir la matemática. Aquí se toca con el dedo toda la diferencia entre inteligencia sensible e inteligencia sentiente de que largamente hablé en la Primera Parte de esta obra. La inteligencia sensible intelige apoyada en los sentidos; la inteligencia sentiente intelige sentientemente todo, tanto lo sensible como lo no sensible" [28]

En el texto, Zubiri destaca, una vez más, el interés filosófico de la matemática (manifestado ya en su tesis doctoral, y que constituye el motor de la presente tesis), dado que la necesidad de dar razón del sentir lo matemático es la que nos pone en la situación de tener que alumbrar una inteligencia que no sea meramente sensible sino sentiente. El sentir lo matemático exige una ampliación de lo ‘sentible’, y esto es posible desde inteligencia sentiente. En efecto, ésta, nos dice Zubiri, intelige sentientemente porque su acto es impresión de realidad, y cuanto intelija se halla inscrito en esta formalidad de realidad sentida.

Como recurso pedagógico, para fijar esta ampliación de la noción de ‘sentir’ según un nuevo paradigma, que consideramos fundamental, lo esquematizamos a continuación:

Sentir "lo sensible"	versus		Sentir "lo real"
Desde inteligencia sensible o sentir puro		Desde inteligencia sentiente o sentir intelectivo
Paradigma de sentir: impresión de las cualidades sensibles		Paradigma de sentir: impresión de la formalidad de realidad física
Sólo se siente el contenido sensible		Se siente realmente el contenido sensible, y el contenido no sensible inscrito en la formalidad de realidad física que nos dan las cosas sentidas.

 

2.3.1 Crítica de la impresión: impresión transcendental de lo matemático.

Lo constitutivo del sentir es la impresión. Por tanto, el comienzo de la epistemología matemática no puede ser otro que la crítica de la impresión que nos habrá de llevar por un "camino seguro" a una nueva fundamentación de la matemática (he aquí la radicalidad del planteamiento de Zubiri). La pregunta ¿cómo habrá que entender la impresión para decir que lo matemático (que no es sensible) se siente? ya quedó planteada en el punto anterior. Puede considerarse que el problema filosófico de la impresión viene exigido, en parte, por la necesidad de fundamentar la matemática y, concretamente, de dar una explicación de las proposiciones que se nos imponen como verdaderas, no obstante ser indecidibles en un sistema formal, con un número finito de axiomas, que contenga la aritmética (Teorema de Gödel).

El análisis zubiriano de la impresión es el siguiente: críticamente, nos dice Zubiri que la idea de impresión viene falseada por la tradición filosófica europea desde los griegos y el propio Kant maneja acríticamente esta noción. Este hecho, que tiene su raíz en la dualidad erróneamente establecida entre sentir e inteligir, tiene una gravísima repercusión para la comprensión de la naturaleza de lo matemática.

"Como toda la filosofía precedente, Kant recibe sin crítica la idea de impresión sensible como mera afección subjetiva; pero le falta el momento de impresión de realidad. La Crítica no tendría que haber sido ante todo una crítica del conocimiento, sino una crítica de la impresión misma" .[29]

Dicho en este momento de paso, lo trataremos más adelante, de aquí hay que partir para mostrar la deficiencia del constructivismo sensible de Kant. La impresión se ha considerado (ya hemos dicho que por situarse desde la perspectiva de inteligencia sensible) como afección subjetiva, como mera impresión del contenido o de las cualidades sensibles. Esto es así, pero insuficiente. Zubiri señala (desde la perspectiva de inteligencia sentiente) que no sólo tenemos impresión de las cualidades sensibles (según los distintos sentidos) sino que también tenemos impresión de la realidad de esas cualidades sensibles. Ésta no debe entenderse como una impresión añadida a la impresión de las cualidades sensibles, sino que se trata de la misma impresión. La diferencia está en que la impresión del contenido de realidad es específica mientras que la impresión de la formalidad de realidad es inespecífica. Este carácter inespecífico le confiere su apertura y transcendentalidad, y le permite ser numéricamente idéntica para los distintos contenidos que aportan los diferentes receptores. Es impresión de realidad no por el carácter de ningún sentido sino por el carácter intelectivo del sentir, pero al ser la inteligencia sentiente es por lo que sólo puede aprehender la realidad de un modo sentido.

Entre realidad y sentir humano (no "puro sentir" como sería el del animal, ni sentir "del hombre", sino sentir intelectivo que es el propio del ser humano) hay, en el pensamiento de Zubiri, una unidad total. Podemos decir: todo lo real presente se siente y todo lo sentido es real. Inevitablemente nuestra mente evoca el polo opuesto de esta postura y es la famosa frase hegeliana: Todo lo real es racional y todo lo racional es real; esto nos llevaría a decir que la razón pone lo real; aún dejando de lado que la razón no es conceptiva sino que es sentiente, desde el planteamiento de Zubiri, esta concepción es incorrecta. Zubiri rechaza el racionalismo y el idealismo en todos los ámbitos, incluido el matemático. ¿Qué nos indica la asociación sentir- realidad ? Realidad la describe Zubiri como formalidad del "de suyo", "en propio", y, en este sentido es una formalidad que se opone a estímulo. Pero hay otro carácter de la realidad, en rigor no cabe decir que sea otro sino el mismo, que nos da la clave de lo que es sentir, se trata del "dar-de-sí" físicamente (no entendido meramente como dinamismo sino que viene a expresar lo que antes significamos al recoger las palabras de Zubiri de que realidad es "donación"). Ahora puede verse que la realidad es donación porque es una estructura que "de suyo" "da-de-sí"[30] . Este giro significa que la razón no pone la realidad física sino que la realidad física se impone al sentir. En conclusión, lo real es lo dado físicamente (impuesto) y el sentir es el recibir impresivamente. Esto tiene su contrapartida y es la siguiente: lo irreal es lo producido (puesto) y el inteligir puro es el concebir.

Si la inteligencia no fuese sentiente podría aprehender la realidad directamente (así lo entendió Platón), pero la inteligencia es sentiente y sólo impresivamente puede aprehenderla. De ahí todo el esfuerzo que tiene que realizar para conocer (que es un despliegue racional de lo ya aprehendido impresivamente en "la" realidad). La formalidad de realidad nos es dada impresivamente en la aprehensión primordial. Es una dimensión física. Queda por aclarar cómo es real el objeto matemático y cómo su realidad es dada impresivamente. Adelantando ideas que explicaremos con mayor detalle posteriormente, diremos que el contenido libremente postulado del objeto matemático se proyecta en "la" realidad campal (esto es la construcción sentiente matemática), de este modo resulta la realidad matemática realizada por postulación constructiva. El problema del sentir la realidad matemática se concreta entonces en el problema del sentir "la" realidad campal.

"Tales son los objetos matemáticos: son objetos reales constituidos en el momento físico de "la" realidad campal, la misma realidad según la cual son reales las cosas como esta piedra. El momento de realidad es idéntico en ambos casos; lo que no es idéntico es su contenido y su modo de realidad".[31]

¿Cómo sentimos el momento físico de "la" realidad campal? Toda aprehensión primordial es impresión de lo real compactamente en su formalidad individual y campal. En la aprehensión diferencial, el momento campal ciertamente puede funcionar con autonomía respecto del momento individual, en tanto que es ámbito trascendental, pero ¿significa que no sea un momento de la aprehensión primordial de realidad y, por tanto, sentido en ella? De ningún modo puede olvidarse que nos es dado en la impresión de realidad de cualquier cosa real. Transcribimos un texto de Zubiri que es clave, a nuestro modo de ver, para clarificar el término impresión referido a lo matemático, entendido en su dependencia con el término impresión de la realidad campal.

"La campalidad es un momento de la aprehensión primordial de realidad; que pueda funcionar con autonomía respecto del momento individual no significa que sea independiente de la aprehensión primordial. Este momento nos está dado allí donde lo real mismo nos está dado: en la impresión de realidad. La impresión de realidad es, pues, aprehensión primordial sentiente de lo real en su formalidad individual y campal: es impresión transcendental "[32]

La campalidad, o realidad campal es dada en aprehensión primordial. Explícitamente señala Zubiri que el momento campal de la realidad es una impresión transcendental. Esto es crucial para la matemática, porque si sobre ella construimos por postulación el contenido creado, "según conceptos", del objeto matemático, por ejemplo, del espacio de Hilbert, el resultado será una realidad física sentida, pero desde luego no sensible. Podemos decir que del espacio de Hilbert tenemos impresión trascendental, sentimos que es "de suyo", sentimos que es real, se nos impone con la fuerza de su realidad, pero, repetimos, no tenemos impresión sensible. Esto nos sugiere la división en la noción de impresión de dos tipos distintos: impresión transcendental (del contenido no-sensible en formalidad de realidad) e impresión sensible (del contenido sensible en formalidad de realidad). Insistimos en que el origen de la impresión transcendental es el mismo que el de la impresión sensible y no se daría sin ésta, lo cual no implica que se reduzca a ella. Transcribimos un texto para que se vea que Zubiri, si bien de forma implícita, da a entender que existe esta distinción en los tipos de impresión, que nosotros establecemos como impresión sensible e impresión transcendental. Con un ejemplo, el color azul lo aprehendemos en impresión sensible, por el contrario, el espacio de Hilbert lo aprehendemos en impresión transcendental.

"Por tanto un objeto matemático no es real por su mera definición ni por su ejecución, pero tampoco es un objeto real en y por sí mismo como las cosas aprehendidas en impresión sensible. Es algo real por un postulado que realiza un contenido (notas y existencia) libremente determinado gracias a la postulación"[33]

Cuando Zubiri habla de "las cosas aprehendidas en impresión sensible " excluye totalmente a los objetos matemáticos. Un objeto matemático no es una cosa aprehendida en impresión sensible. Por ello, la pregunta ¿hay aprehensión primordial del objeto matemático, como lo hay de las cosas físicas? La respuesta es contundente: No, los objetos matemáticos no se nos dan en aprehensión primordial, y la razón es que no son realidades "en y por sí mismas" (que, como señala el texto, son las únicas que se dan en la aprehensión primordial) sino que son realidades con un contenido postulado, son realidades "en y por postulación". Ahora bien, decir que los objetos matemáticos no se aprehenden en impresión sensible o aprehensión primordial ¿equivale a negar el carácter sentido al objeto matemático, esto es, a afirmar que es meramente no-sentido? De ninguna manera. Esto se aclara con lo que venimos diciendo: de los objetos matemáticos no hay impresión sensible sino impresión trascendental, que en cuanto impresión es sentida. Por otra parte se ve también que si el término del sentir es la realidad, son los distintos tipos de realidad (más propiamente los distintos tipos de contenido de realidad, porque la formalidad de realidad es numéricamente idéntica en todos los casos) los que especifican los distintos tipos de sentir. Son dos:

 

1. Las realidades con un contenido dado son sensibles, y las aprehendemos en impresión sensible.

2. Las realidades con un contenido construido libremente no son sensibles (son más bien sentibles) y las aprehendemos en impresión transcendental.

 

Podemos objetar, que en el espacio de Hilbert o cualquier objeto matemático se siente no sólo la formalidad de realidad (impresión transcendental) sino también el contenido de realidad, e impresiona el contenido en formalidad de realidad. Hay que afirmar, para no desvirtuar el pensamiento de Zubiri, que la formalidad no se puede dar independiente de un contenido (independiente de un contenido determinado, pero no de todo contenido). Sentimos el contenido en formalidad de realidad del espacio de Hilbert, pero un contenido que no es sentible por y en sí mismo (por eso no es sensible sino conceptual) sino en cuanto realizado en la impresión de realidad. Creemos que puede decirse, en la línea de Zubiri, que sentimos el espacio de Hilbert "en y por sensibilización" postulada en la impresión de realidad dada en aprehensión primordial, en cuanto que impresión. Si el espacio de Hilbert se inscribe en la impresión de realidad, a su modo es sentido.

Zubiri no explicita la distinción entre lo sentido "en y por sí mismo" y lo sentido "en y por postulación en la impresión de realidad"; seguramente porque ya está implícita en la distinción que hace entre realidades "en y por sí mismas" y realidades "en y por postulación" en la impresión de realidad. Observamos que al igual que esta distinción evita deslizarse del tipo de realidad matemática al tipo de realidad de las cosas físicas, la distinción paralela en el sentir evitaría deslizarse del tipo de sentir los objetos matemáticos al modo de sentir los objetos físicos. Zubiri insiste en que no se sienten del mismo modo las realidades "en y por sí mismas" y las realidades "en y por postulación", la diferencia estriba en que en el primer caso tenemos impresión inmediata y en el segundo caso tenemos impresión por "sensibilización". La construcción matemática, creemos, que debe afirmarse como un proceso de realización e idénticamente como un proceso de sensibilización. (Hacemos uso del vocablo que existe, pero entiéndase en la acepción de sentible y no sensible). Si Zubiri no explicita este segundo momento es, como ya hemos dicho, porque se sobreentiende en la noción de realización, pues la realidad sólo se nos da en impresión de realidad. Presentamos esquemáticamente, esta diferenciación fundamental.

Tipos de impresión de realidad	Momentos de la realidad
	El contenido	la formalidad
1. Impresión sensible.	las cualidades sensibles	formalidad abierta
De cosas reales "en y por sí mismas". ( sensibles "en y por sí mismas)		carácter del "de suyo"
	es sentido "en y por sí mismo", nos es dado en aprehensión primordial	es sentido, dado en aprehensión primordial
2. Impresión trascendental	contenidos construidos	formalidad abierta
De cosas reales " en y por postulación" (sentibles en y por postulación)		carácter del "de suyo"
	Es sentido en cuanto sensibilizado en la impresión de realidad	Es sentido, dado en aprehensión primordial por las cosas

 

El sentir en las cosas físicas y en los objetos matemáticos es idéntico en la impresión de la formalidad de realidad, son distintos en el contenido de realidad; por lo mismo que son realidades idénticas en la línea de la formalidad pero distintas en la línea del contenido y su modo de realidad. Zubiri mantiene la noción de sentir que nos lega la tradición, en cuanto que lo sentido es lo dado o impuesto impresivamente en aprehensión sensible frente a lo concebido o construido por el sujeto. La originalidad de Zubiri no está en que tenga una noción de sentir distinta (lo que nos parece que tiene que ahorrarnos entrar por la vía de buscar un significado nuevo a qué sea sentir en este autor), sino de qué siente una inteligencia sentiente a diferencia de una inteligencia sensible. El propio Zubiri, como ya señalamos, decía que en el sentir matemático se tocaba con el dedo toda la diferencia entre inteligencia sensible e inteligencia sentiente. Desde inteligencia sentiente, vemos que en la aprehensión primordial de las cosas "en y por sí mismas" se nos da impresivamente tanto el momento de formalidad de realidad como el momento del contenido. Por el contrario, en las realidades "en y por postulación" no nos es dado el contenido en la aprehensión (por eso será postulado), sino que sólo se da o se nos impone impresivamente el momento de formalidad de realidad, y sólo al realizar el contenido creado en esta impresión de realidad sentimos que el contenido se nos da impresivamente, se nos impone con la fuerza de lo real. Vemos, pues, la repercusión que tiene la concepción zubiriana de la inteligencia sentiente en la epistemología matemática; sólo desde una inteligencia sentiente puede hacerse esta distinción entre contenido y formalidad, y sólo una inteligencia sentiente puede sentir el contenido y la formalidad de realidad, y, por último, sólo una inteligencia sentiente puede sentir todo lo real sea sensible o construido. Este es el resultado que arroja la crítica de la impresión desde inteligencia sentiente, frente al resultado legado por la tradición desde inteligencia sensible.

Como conclusión, y dada la gravedad de esta cuestión para entender toda la epistemología matemática de Zubiri, recogemos las ideas fundamentales a modo de tesis sustentadas por los textos del propio Zubiri desde su perspectiva de inteligencia sentiente.

1. Sentir no es aprehender meramente lo sensible, sino que es aprehender lo real en impresión. El término respectivo a sentir no es lo sensible sino lo real.

"¿Pero ¿qué es sentir? Es desde luego la presentación de algo que en una o en otra forma tiene un momento de realidad".[34]

"...sentir es aprehender lo real en impresión"[35]

2. Los objetos matemáticos, por ejemplo, un número transfinito, no es una cualidad sensible, pero es algo real, y como tal se sienten.

"Un número transfinito, un concepto abstracto, no son cualidades sentidas. Pero son inteligidas como algo real, y a fuer de tales se constituyen en la impresión de realidad en cuanto tal".[36]

3. Los objetos matemáticos no se sienten por sí mismos como los objetos sensibles, pero se sienten "por estar inscritos en la formalidad de realidad dada en impresión ".

"...todo objeto matemático está inscrito en la formalidad de realidad dada en impresión. Es decir, es término de una intelección sentiente. No se trata de que un espacio geométrico o un número irracional sean sentidos como se siente un color; esos objetos evidentemente no son sensibles. Se trata de que el modo de intelección de un número irracional o de un espacio geométrico es sentiente".[37]

4. La impresión de realidad en la que se aprehenden los objetos matemáticos es la misma de las cosas físicas, idénticamente a como su realidad es la misma.

"El número irracional no se aprehende como un color, pero al igual que el color es aprehendido en la misma formalidad de realidad, en la misma impresión de realidad en la que es aprehendido el color. El número irracional no es igual que un color, pero es real en la misma formalidad de realidad en la que es real el color. Es en ambos casos numeralmente la misma formalidad de realidad". [38]

5. La distinción entre sentir un color y sentir un número irracional está en el contenido, pero no en la formalidad de realidad dada impresivamente. Del mismo modo que los distintos tipos de realidades se establecen por la diferencia de contenido, no por la formalidad de realidad.

"Tampoco se trata de que lo inteligido en el logos sea sentido al igual que un color o un sonido; puedo inteligir en mi logos por ejemplo números irracionales. Pero es que tanto el color como el número irracional pertenecen al contenido de lo inteligido, mientras que la intelección misma en su modo sentiente concierne no al contenido sino al modo como este contenido queda en la aprehensión".[39]

"El logos es sentiente no por la índole de lo inteligido, sino por el modo de su intelección: es una intelección dentro de la formalidad de realidad sentida"[40]

6. El contenido del objeto matemático, por ejemplo, un conjunto continuo, aunque no se siente puede realizarse de un modo sentiente en "la" realidad, y esto es así por ser la inteligencia sentiente.

"Sólo una inteligencia sentiente puede por ejemplo no sentir el contenido de un conjunto continuo, esto es el conjunto de los números irracionales, y sin embargo realizar libremente este contenido (conceptuado sea por meras definiciones, sea por operaciones ejecutadas) de un modo sentiente" [41]

7. Por ultimo, el modo de intelección de lo matemático es sentiente no porque se sienta el contenido (pensar esto sería un interpretación errónea del pensamiento zubiriano sobre la matemática) sino:

a) Porque los objetos matemáticos se inteligen inscritos en la realidad campal, esto es, en la formalidad de realidad dada en impresión.

b) Porque su construcción no es mera conceptuación (operación conceptiva) sino que es realización , y esto es una operación física y no mental, es una operación sentiente.

"Se trata de que el modo de intelección de un número irracional o de un espacio geométrico es sentiente. Y lo es: 1º porque se inteligen postuladamente en un campo de realidad, esto es en la formalidad dada en impresión de realidad, y 2º porque su construcción misma no es mera conceptuación sino realización, es decir algo llevado a cabo sentientemente"[42]

Acabamos señalando que lo matemático se nos da impresivamente, no "en y por sí mismo" sino por inscribirse el contenido libremente construido en la formalidad de realidad dada impresivamente. Ésta se siente pero no es sensible, transciende todo lo sensible, es impresión transcendental. Pero entonces de los objetos matemáticos no hay impresión sensible sino impresión transcendental. A esto queríamos llegar.

 

2.3.1.1 Análisis estructural de los tres momentos de la impresión del objeto matemático.

Hemos constatado que lo sentido es lo dado impresivamente . Y esto tanto en general como aplicado a la matemática. Nos detenemos ahora un poco más para explicar en qué consiste la impresividad de lo matemático. En este punto se pondrá en evidencia su peculiaridad, habida cuenta del cambio de paradigma de sentir desde sentir lo sensible a sentir lo real y la distinción, que hemos establecido en el punto anterior, entre impresión sensible e impresión transcendental, en la línea del contenido no en la línea de la formalidad. El hecho que de lo matemático tengamos impresión transcendental necesariamente ha de matizar los momentos de su impresión respecto a la impresión de las cosas físicas (no en la línea de la formalidad que es idéntica). Veamos en qué consiste la impresividad de lo matemático.

"He aquí lo formalmente constitutivo del sentir: impresión. La filosofía, tanto antigua como moderna, o bien no ha reparado en esta impresividad, o bien (más generalmente) ha reparado en ella pero sin hacer un análisis de su estructura formal. Se ha limitado a describir las distintas impresiones. Pues bien, es absolutamente necesario conceptuar con rigor qué es impresión, esto es en qué consiste la impresividad. Sólo así podremos hablar del sentir de una manera originaria"[43]

Recordemos que lo matemático, por ejemplo, el espacio de Hilbert, evidentemente, no nos impresiona como este rayo de luz. Pero ya hemos visto que no quiere decir que sea algo pura y simplemente no-sentible. Se aclarará más al examinar cómo se entienden en la matemática los tres momentos de la impresión: afección, alteridad y fuerza de imposición.

a) Afección.

Podemos ver que de algún modo padecemos la impresión de lo matemático. Una vez construido el objeto matemático en "la" realidad, las afirmaciones que hagamos sobre él no son una actividad intelectiva espontánea, sino que penosamente nos tenemos que mover en la realidad misma del objeto para saber lo que es en realidad. Como afección es recepción de algo físico, de inmediato nos formulamos la pregunta: ¿a través de qué receptor padecemos la impresión de lo matemático? La formalidad de realidad sobre la que construimos por postulación el contenido del objeto matemático se nos da por cualquiera de los sentidos. Una vez construido el objeto matemático, el modo de sentir intelectivo que más puede convenir a lo matemático (en realidad a todo movimiento del logos y a toda marcha de la razón, en tanto que logos y razón son "sentientes") es el tantear. Este dinamismo es receptivo como lo es escuchar, palpar, mirar, etc. Como dice Zubiri (refiriéndose a toda afirmación en general):

"Por esto, este movimiento es todo menos un arrebato, porque es todo menos una actividad espontánea mía. Ciertamente, en cuanto tanteo este movimiento me pertenece a mí, y en este sentido se puede decir que soy yo quien afirma. Pero es que este tanteo, aun siendo un dinamismo mío, es un dinamismo meramente receptivo como pueden serlo el mirar, el palpar, el escuchar, etc." [44]

La razón también se mueve en la realidad de lo matemático en forma de tanteo. De este modo, nos es dada impresivamente la realidad matemática de un modo que Zubiri denomina: realidad-tanteada. El tanteo es un andar a tientas, palpando la realidad misma. Dice Zubiri (refiriéndose a la razón en general):

Y el tanteo, ya lo vimos, es un modo de intelección de lo real: el tanteo de la realidad nos da la realidad misma en cuanto "realidad-tanteada", esto es, la realidad en modo de lo tanteable. La razón sentiente es en última instancia razón que se mueve en tanteo..."[45]

Conviene precisar más el tipo de afección de lo matemático, porque no parece que sea del mismo tipo que la afección no ya meramente estimúlica, lo cual se da en el animal (que tiene sentir puro) pero no en el hombre (que tiene sentir intelectivo), sino de la afección de realidad estimúlica. Aquí se ve la diferencia entre la impresión sensible y la impresión transcendental; mientras que en impresión sensible tenemos afección de realidad estimúlica y no en todos los casos, en la impresión transcendental, por tener un contenido no sensible, no tenemos afección de realidad estimúlica. La pregunta que tenemos que plantearnos es: ¿toda afección de realidad es estimúlica?, esto es, ¿toda afección de realidad suscita una respuesta en afección? Zubiri dice que no. Esto aclara enormemente la cuestión referida al objeto matemático.

"Y esta realidad aprehendida no sólo no está estimúlicamente aprehendida, sino que su realidad puede no tener carácter de estímulo. Todo estímulo es aprehendido por el hombre como realidad, pero no toda realidad aprehendida es forzosamente estímulo: un paisaje no es necesariamente estímulo, ni lo es tampoco un sonido elemental. Afectados así por lo que es "en propio", la afección misma es afección real".[46]

Así pues, de un espacio de Hilbert, por ejemplo, no tengo afección estimúlica, tampoco tengo afección de realidad estimúlica, sino que tengo meramente afección real. Estoy afectado por el espacio de Hilbert en cuanto es "en propio", "de suyo". Si se admite esta matización zubiriana, ya no tiene sentido preguntarnos ¿cuál es el estímulo físico que me impresiona en el espacio de Hilbert? Insistimos, la realidad aprehendida en el caso del espacio de Hilbert, o de cualquier objeto matemático, no es estímulo, no es realidad estimúlica. Y es que sentir no tiene porqué estar relacionado con un estímulo físico. Con lo que está relacionado el sentir es con una realidad física que nos tiene que ser dada en impresión. El espacio de Hilbert es realidad física, y me afecta realmente pero no estimúlicamente. Pero la cosa es muy distinta.

En Zubiri hay una ampliación del horizonte de lo que se ha entendido en la filosofía clásica por afección. La afección no supone necesariamente un estímulo físico ni materialidad que impresione alguno de mis once sentidos. Lo que sí supone es realidad, del modo que sea, y recordamos que realidad es formalidad física dada en aprehensión primordial (no lo existente fuera de nuestra aprehensión). Humanamente hablando, si algo no es real no puede afectarnos, y, por el contrario, si algo real está presente en nuestra aprehensión necesariamente me afecta. La formalidad de realidad nos es dada, adviene a mi intelección por la aprehensión primordial de realidad (única vía por la que es posible) y yo padezco esta impresión. No es algo que haya sido concebido por mí. Si echamos una mirada comparativa al idealismo de Kant, observamos que, según Zubiri, no es el sujeto el que pone la condición de posibilidad de la sensibilidad sino que es la propia realidad la que se la tiene que dar.

b) Alteridad

La alteridad en la impresión de lo matemático nos presenta aquello que nos impresiona, según una formalidad dada y un contenido postulado. Podríamos pensar (así se ha hecho desde la inteligencia sensible) que nos impresiona una cualidad sensible, y en este sentido el objeto matemático no podría tener el carácter de aquello presente por lo que somos impresionados. Pero, volviendo a la ampliación de horizonte zubiriano, hay que decir que no se trata de nota sensible sino de nota real. Zubiri (desde la inteligencia sentiente), para evitar la reducción de lo real a lo sensible, denomina a todo lo que está presente en la impresión: "nota". Es fundamental, pues, tener en cuenta que nota es todo aquello que está presente en la impresión (gnoto), y no es sinónimo de cualidad sensible, porque hay notas que no son cualidades sensibles. Esta especificación zubiriana permite considerar al objeto matemático, que no es una cualidad sensible, como una nota, en el mismo sentido en que lo es la cualidad sensible, aunque sus contenidos sean distintos. Por ejemplo, el número tres, no es nota de índole cualitativa (es cuantitativa), pero sí es nota real. Y un espacio de Hilbert es nota (sistema de notas) en cuanto algo presente en mi impresión de realidad (no "en y por sí mismo", pero sí "en y por postulación") Nos dice Zubiri:

"...pero la nota no es siempre de índole cualitativa. Si veo tres puntos, "tres" no es una cualidad. Pero es nota... Es verdad que muchísimas veces llamo a las notas cualidades, pero es en sentido lato. En sentido estricto nota no es cualidad, sino algo meramente noto; es pura y simplemente lo presente en mi impresión" [47]

En este texto hay algo sobre lo que queremos llamar la atención. Aquí el número natural "tres" es puesto por Zubiri como ejemplo de algo gnoto, pero como algo dado igual que se nos da, por ejemplo, el color "verde", esto es, sin ser resultado de ninguna operación. ¿Quiere esto decir que los números naturales se nos dan en aprehensión primordial igual que se nos dan las cosas en y por sí mismas?. No es algo desarrollado en Zubiri, pero teniendo en cuenta lo expresado, podemos pensar que este autor se uniría a la famosa afirmación de Kronecker, que él mismo recoge en Inteligencia y Logos (p. 140): "Dios creó el número entero y lo demás lo han creado los hombres". El número entero sería un dato de la aprehensión primordial de realidad tanto en su contenido como en su formalidad. En lo que ya no está de acuerdo Zubiri con Kronecker es en considerar que "por consiguiente construir se reduciría en última instancia a contar lo dado" (ibid). Es toda la diferencia, como veremos, entre la concepción de construcción intuicionista y la de construcción sentiente. La inteligencia sensible intelige apoyada en los sentidos, en cambio la inteligencia sentiente no.

La alteridad además del contenido tiene el momento de formalidad de realidad, como repetimos constantemente, es un momento dado, sentido, es el modo de "quedar" el contenido. El término "quedar", designado por Zubiri para la realidad, es suficientemente expresivo de la receptividad del sujeto frente a la realidad. El "quedar" es un mecanismo receptivo. La formalidad de realidad es el modo de "quedar" el contenido "de suyo", "en propio". El sujeto no produce en absoluto la realidad, le es dada a través del sentir. No debe confundirse formalidad en Zubiri con lo que Kant denominaba forma a priori, ni con la forma tal y como la entiende la Gestalt (psicología de la forma). Zubiri mismo se encarga de hacer netamente la distinción.

"Formalización no es, pues, ni información ni configuración, sino autonomización: es cómo "queda" el contenido. La formalidad no está producida por el sentiente (Kant), ni es configuración primaria (Gestalt). Es pura y simplemente modo de quedar"[48]

La autonomía con la que quedan los objetos matemáticos, en cuanto realizados en la impresión de realidad dada en aprehensión primordial, es lo que ha podido inducir a pensar que son independientes totalmente del sujeto y pertenecen al Mundo de las Ideas (Platón), pero esto tampoco es así en Zubiri. Según este autor son independientes del sujeto, pero es una independencia transcendental no transcendente; se constituyen en la impresión de realidad dada en aprehensión primordial de realidad.

c) Fuerza de imposición.

Este tercer momento es clave y lo veremos más detenidamente en el estudio de la realidad de lo matemático. ¿Cómo se nos impone lo matemático? Que este libro se me impone está claro, lo miro y no puedo dejar de verlo por más que mi voluntad deseara ver otra cosa en su lugar; hay una imposición de su realidad. ¿Ocurre lo mismo con el espacio de Hilbert?, ¿no es una construcción mía y en cuanto tal un acto espontáneo que puedo libremente modificar? Veamos.

Según Zubiri, la construcción matemática es sentiente, y esto quiere decir que hay dos momentos en todo objeto matemático: 1. de espontaneidad (construcción), y 2. de imposición (sentiente). Es decir, la creación de un ente matemático aún siendo el acto de máxima libertad, como analizaremos en el siguiente capítulo, no es totalmente espontáneo. Ni antes ni, por consiguiente, después de su construcción. El hecho es que la creación en su momento de espontaneidad, momento subjetivo, actúa llamando intrínsecamente un momento de objetividad que es el que le va a dar el momento de impresión, de sentido, porque de lo contrario no habría imposición. Si la inteligencia fuese concipiente podría ser totalmente espontanea, de tal modo que no sentiría lo producido por ella, y no recibiría ningún tipo de imposición. Pero no es esto lo que constatamos, ni en general ni en la matemática.

El matemático cuando construye postuladamente en "la" realidad los objetos matemáticos siente que hay propiedades que no son postuladas ni deducidas del sistema y sin embargo, "se le imponen, le llevan, le arrastran" en virtud de las propiedades que tiene por haber sido realizados en la realidad. Hemos elegido libremente unos axiomas, sí pero una vez construidos postuladamente va a aparecer otro que no es subjetivo sino que es objetivo y se nos va a imponer (aunque no son por postulación tampoco son en y por sí mismos, sino por la postulación de los otros caracteres de lo matemático, por eso no son tampoco sensibles). Los objetos matemáticos, en cuanto realizados, tienen propiedades o notas "suyas", "propias" que nos plantean problemas que no tiene solución desde el sistema de axiomas y postulados que han posibilitado su realización. Este es el significado del Teorema de Gödel.

Esta idea de la fuerza de imposición de la realidad matemática es sobradamente apoyada, incluso en el uso de los vocablos, también en la matemática por el denominado método de forzamiento[49]. Es el método usado en 1963, por P.J. Cohen para demostrar la consistencia de la negación de la hipótesis generalizada del continuo y del axioma de elección relativamente al sistema de axiomas de Zermelo-Fraenkel. Este método ha resultado de una fecundidad incluso mayor que la del método de los conjuntos constructibles de Gödel para resolver cuestiones metamatemáticas. Zubiri tenía bien presente este método de forzamiento al referirse a la fuerza de la realidad de lo matemático. En Inteligencia y Logos menciona los dos tipos de propiedades de los conjuntos que distingue Cohen (Cohen) y los interpreta como expresión de la fuerza de realidad,

"Unas, que son específicas, las que responden a los postulados y axiomas operacionales a que acabo de referirme. Otras propiedades son más bien genéricas, en virtud de las cuales forman un conjunto dejando indeterminadas las propiedades específicas, las cuales "forzarán" a las propiedades genéricas a especificarse"[50]

La fuerza de imposición de la realidad tiene tres formas distintas, según las modalizaciones de la inteligencia sentiente: 1. la fuerza irrefragable de realidad (en aprehensión primordial), 2. la fuerza exigencial de lo real (en el logos sentiente), 3 la fuerza coercitiva de lo real (en la razón). En concreto en la matemática, los objetos matemáticos constituidos en la impresión de realidad dada en aprehensión primordial de realidad nos imponen propiedades "de suyo", no postuladas por mí; la realidad de lo matemático aprehendido nos impone no sólo unas notas sino unas exigencias de lo que serían en realidad, su realización constituirán las evidencias; la fuerza coercitiva de la realidad profunda se nos impone de tal modo que tampoco podemos postular arbitrariamente su contenido. Esto lo desarrollaremos más adelante.

La conclusión de este análisis de la estructura de la impresión de lo matemático muestra que existe una matemática sentiente, desde el punto de vista zubiriano, frente a una matemática concipiente.

 

2.3.2 Sentir lo matemático: condición necesaria para la construcción matemática.

Volvemos a retomar la frase de Zubiri: "sin sentir lo matemático, no se puede construir la matemática". ¿A través de qué se nos da el momento de formalidad de realidad o el "de suyo" del objeto matemático en la aprehensión primordial? De nada especial, sino de cualquier cosa sentida. Es idéntico el momento de realidad de esta piedra y del continuo, consiste en el carácter abierto o el "más" de toda cosa real en y por sí misma. La formalidad de realidad de lo aprehendido en y por sí mismo es "más" que lo que es por este determinado contenido, de hecho aunque sus notas concretas varíen sigue siendo "el" mismo, aunque no "lo" mismo. Ese "más" es lo que permite que se postule un libre contenido en ella.

Esquemáticamente:

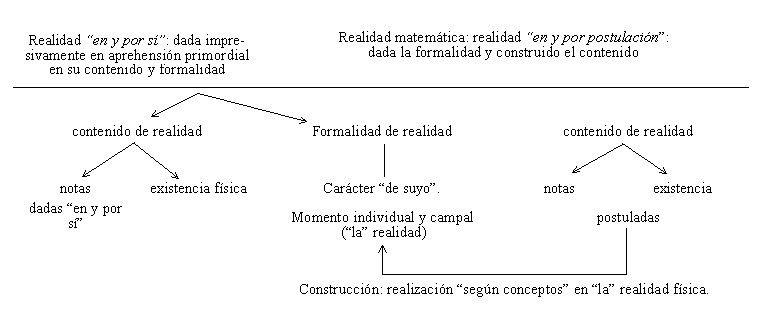
Repetimos, una vez más, dada la importancia de esta cuestión, que de los dos momentos de la aprehensión primordial de las realidades en y por sí mismas el decisivo en la impresión o sentir es el de la formalidad de realidad, y no en su dimensión individual sino en su dimensión campal que es "el ‘de suyo’ autonomizado"[51]. En ella se realiza el contenido construido de los objetos matemáticos. La cuestión sobre la que se apoya todo el peso o la fragilidad (no entramos ahora en ello) de la concepción zubiriana de la naturaleza de la matemática es la siguiente: este momento campal ¿es dado o concebido? Depende de esta respuesta el carácter sentiente o el carácter lógico de la matemática. Zubiri no es ajeno a la gravedad de esta cuestión pues no ahorra todo tipo de explicaciones en la I parte de Inteligencia y Logos, para asentar definitivamente el carácter físico de la realidad campal, y, por tanto, dado en la impresión sensible, por ser la inteligencia sentiente, esto es, que siente las cualidades sensibles y siente "la" realidad.

Sin sentir la realidad o sin que ésta nos sea dada impresivamente no tendríamos juicios de realidad ya sea campal o mundanal, lo único que tendríamos es un conjunto de conceptos de realidad pero de éstos nunca podríamos dar el salto a la realidad. Los juicios nunca nos llevan a la realidad sino que la presuponen, se mueven ya en ella. Esto parece claro en las cosas reales "en y por sí mismas", pero no en las cosas realizadas constructivamente; bien, éstas suponen la postulación, pero ésta sólo es postulación en cuanto fundada en aprehensión primordial. El siguiente texto de Zubiri es explícito:

"Así pues, todo juicio, toda afirmación, lo es de algo real presupuesto como tal a la afirmación, lo es de algo real presupuesto como tal a la afirmación misma. Cuando las cosas son reales en y por sí mismas, aquella presuposición es formalmente la aprehensión primordial de realidad. Cuando las cosas son reales, pero realizadas constructivamente, entonces la presuposición es formalmente postulación. La postulación es posible sólo por estar intrínseca y formalmente fundada en la aprehensión primordial de realidad" [52]

Gráficamente:

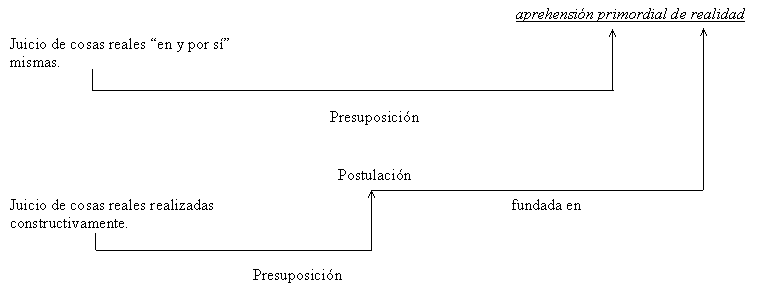
La aprehensión primordial de realidad de las cosas reales "en y por sí mismas" es el supuesto de la postulación de la realidad matemática. Postulamos el "contenido" de la realidad matemática que como tal realidad (formalidad) nos es dada en impresión de realidad por cualquier cosa física (en su momento campal). El contenido del objeto matemático es realidad sentida tan sólo por ser contenido de la impresión de realidad .[53]

Una vez justificada la postura sensista de Zubiri, es preciso señalar el gravísimo error en el que incurriríamos si confundiésemos el sensismo de la matemática con el sensualismo de la matemática. En Inteligencia Concipiente no existe esta distinción entre sensismo y sensualismo porque no se distingue formalidad y contenido. Ahora bien, desde inteligencia sentiente, su diferencia es neta: el sensismo es una postura en la línea de la formalidad de realidad, el sensualismo es una postura, por el contrario, en la línea del contenido de la realidad. Zubiri no afirma de ningún modo que los objetos matemáticos sean sensibles sino, en todo caso, sentibles. El sensualismo es una reducción en el contenido. El contenido de la matemática se reduciría al contenido de las impresiones sensibles (más o menos generalizado, poco importa).

Definimos a continuación la postura sensista de Zubiri al hilo de su oposición a la postura sensualista que nosotros concretamos en:

1. J. S. Mill y

2. Feyerabend.

 

2.3.3 Sensismo de Zubiri frente al sensualismo de J.S. Mill

Mill[54] desde su postura empirista[55] considera que la matemática es una elaboración a partir de los datos de la experiencia. Dice:

"¿Por qué las matemáticas y aún las ramas de las ciencias naturales que por las matemáticas han llegado a ser deductivas, se han considerado por los filósofos como independientes de la experiencia y de la observación y como sistema de verdades necesarias? La respuesta es, creo, que este carácter de necesidad asignado a las verdades de las matemáticas... son una ilusión que no se mantiene sino suponiendo que estas verdades se refieren a objetos y a proposiciones de objetos puramente imaginarios".[56]

Frente a la concepción racionalista de la matemática, Mill opone su concepción empirista de la matemática, según la cual ésta no trata de objetos imaginarios sino que "tiene por objeto las líneas, los ángulos y las figuras, tal como existen"[57], son representaciones de las cosas observables. El sensualismo de Mill le lleva a poner como base de todo nombre abstracto una sensación: "todos los nombres deben serlo de alguna cosa; no hay nombres abstractos. Diez debe significar diez cuerpos, o diez sonidos, o diez pulsaciones"[58] . La suma de 7+5= 12, considera que no es un juicio analítico sino que también es un hecho de experiencia; se trata de agrupaciones de cosas que impresionan los sentidos. Por el método inductivo pasaríamos de las proposiciones individuales de los objetos matemáticos a lo general y abstracto. Resultado de este método son las definiciones y los axiomas. Así dice Mill del axioma que es "una generación de la observación"[59]. Las demostraciones matemáticas tienen carácter deductivo, pero éste se apoya en última instancia en inferencias inductivas.

¿Qué cabe decir de la postura "empirista" de Mill a la luz de la concepción zubiriana de la matemática? Lo analizamos en distintos puntos:

1. Parte de una inteligencia sensible, y esto quiere decir que el objeto adecuado de ésta es lo sensible, las cualidades sentidas; y que todo cuanto intelige tiene un estricto apoyo en los sentidos. Es incorrecto, porque la inteligencia es sentiente y siente lo real aunque no sea sensible.

2. Esta perspectiva le conduce al "sensualismo" en matemáticas, esto es, a la reducción del contenido racional al contenido de las impresiones sensibles. Lo cual, para Zubiri, es absurdo. Y la desviación del sensualismo lo confirma también las distintas geometrías no-euclídeas, hecho éste que a pesar de ser contemporáneo de Mill le pasa desapercibido[60].

3. La concepción que tiene Mill de impresión sensible está viciada con el mismo error que Zubiri atribuye a toda la tradición filosófica: se ha resbalado totalmente sobre el momento de formalidad de realidad sentida y sólo se ha fijado en el momento del contenido de realidad.

Zubiri rechaza, pues, rotundamente el sensualismo. Considera que el contenido de la razón sentiente es irreductible al contenido de las impresiones sensibles. Aplicado al objeto matemático hay que decir que éste no se funda en el contenido de la impresión sensible, ya hemos dicho que es libremente postulado, sí que se funda, por el contrario, en el momento de formalidad de la realidad aprehendida primordialmente.

"Al decir, pues, que la razón no es sólo sensible sino sentiente, no se trata de una reducción sensualista de la afirmación y de la razón. Porque "sensualismo" significa que los contenidos del juicio y de la razón se reducen formalmente a los contenidos de las impresiones sensibles. Y esto es sencillamente absurdo. Es que la filosofía no ha visto en las impresiones sensibles más que su contenido, y ha resbalado sobre su formal momento sentido de realidad: no ha visto la impresión de realidad"[61].

Y tras este alejamiento del sensualismo precisa su postura "sensista",

"Pero queda el momento formal de realidad, la impresión de realidad. Y entonces, reducir el momento de realidad de la afirmación y de la razón a la realidad sentida en impresión, a la impresión de realidad, no es sensualismo. El momento de realidad propio de la afirmación y de la razón es física y numéricamente idéntico al momento de realidad impresivamente aprehendida en aprehensión primordial... La unidad física y formal del momento de realidad como impresión no es por tanto sensualismo. Es más bien, sensismo"[62]

Esta distinción entre "sensismo" y "sensualismo" es fundamental para no interpretar mal el pensamiento de Zubiri. Cuando nos dice que el objeto matemático es sentido defiende un "sensismo" y no un "sensualismo", esto es, hay una reducción de la construcción matemática a lo sentido en la línea de la formalidad de realidad campal que es idéntica, pero ni mucho menos en la línea del contenido. Mas aún, nos dirá Zubiri, que en la línea del contenido no tiene nada que ver la realidad sentida en impresión sensible y la realidad matemática:

"La realidad matemática no es una parte o un momento de la realidad campal; nada tiene que ver con ésta por razón de su contenido. Pero esta nueva realidad, en cuanto realidad no sería postulada si la razón no se moviera ya en la realidad campal en cuanto realidad. Es esta realidad física misma en cuanto realidad la que constituye aquello de lo que se postula el contenido".[63]

A continuación Zubiri señala cómo es esta independencia del contenido de la realidad campal la que nos fuerza a esbozar libremente un sistema de postulados. Estos postulados son el contenido real de la impresión de realidad dada en aprehensión primordial.

"Aquí la realidad campal en cuanto realidad es un sistema de referencia según el cual la realidad misma tiene un contenido formalmente independiente de todo su contenido campal. Y esta independencia es justo un modo referencial, el modo de referirnos a la realidad campal "independientemente". Esta independencia nos fuerza a esbozar un libre sistema de postulados o axiomas(...) Estos postulados son pues la determinación postulada del contenido de la realidad, una realidad numéricamente idéntica a la realidad campal en cuanto realidad"[64].

Según Zubiri, frente a todo sensualismo, la matemática no sale de la experiencia, en el sentido usual de la palabra. El contenido de los objetos matemáticos es independiente del contenido de los objetos que percibimos, ya hemos visto que no hay aprehensión primordial de los objetos matemáticos. Se opone rotundamente a la concepción de Mill que los considera representaciones de los hechos de observación. Zubiri sostiene que el contenido es una libre postulación. Ahora bien, ésta es posible porque nos movemos en la realidad campal sentida. Como ya señalamos sólo porque sentimos esta impresión de realidad podemos construir por postulados y axiomas el contenido.

 

2.3.4 "Ingenuidad" del sensualismo de Feyerabend.

El sensismo de la matemática (y de cualquier intelección racional) defiende que sentimos la formalidad de realidad dada en aprehensión primordial, y, a la vez, exige un aumento del contenido de la construcción matemática respecto del contenido de la aprehensión primordial; y esto en oposición a la reducción del contenido de la realidad profunda al contenido de la realidad campal, a la que nos conduce el sensualismo.

Este apunte crítico nos lleva a considerar a Zubiri un interlocutor válido en un hipotético diálogo con el filósofo de la ciencia Feyerabend a raíz de la polémica establecida con su artículo: "Una lanza por Aristóteles. Anotaciones al postulado del aumento del contenido " Utilizando las expresiones zubirianas podemos ver que este autor identifica el mundo (en el sentido amplio de realidad profunda) con el campo, y en esta reducción consiste toda la ingenuidad del conocimiento matemático, y de la ciencia en general. Según Zubiri:

"Todas las ‘ingenuidades’ de la razón se reducen a una misma cosa: a pensar que el mundo es formalmente idéntico a lo sentido de él, al campo. El campo sería entonces la estructura formal del mundo. Y en esto estriba la ingenuidad. El campo no es de por sí estructura del mundo sino mero sistema de referencia. Y lo es porque el campo es real. Lo que sucede es que es tan sólo campalmente real"[65]

Feyerabend[66], en su crítica a la exigencia de profundidad propugnada por el Racionalismo Crítico de Popper y Lakatos (exigencia que es defendida igualmente por Zubiri), comete el error, desde la perspectiva zubiriana, de reducir el contenido mundanal o realidad profunda al contenido campal. En el artículo mencionado expone los argumentos que Aristóteles presentó contra la búsqueda de una profundidad mayor en la explicación y cuales son sus consecuencias:

"Ir a fundarse más allá de los fenómenos significaría aquí fundarse más allá de las formas que se encuentran en la conciencia y esto equivaldría a pretender fundarse más allá de las formas de la naturaleza, lo que equivaldría a alejarse de ella. Eso vendría a suponer que la Naturaleza no es lo que es y con eso se habría introducido el error"[67]

Considera Feyerabend, que a un aristotélico tiene que parecerle completamente absurda la búsqueda de lo "profundo" tras las percepciones. Todo intento de este tipo supone que el mundo tiene otra forma de la que realmente tiene.

"Se busca detrás del mundo real un segundo mundo oculto, a pesar de que ese mundo real sea completo en sí mismo. Y esa búsqueda se emprende no porque alguna observación del mundo real se haya encontrado con problemas, sino solamente porque se quiere satisfacer un sueño filosófico. Este es el summun de la irracionalidad"[68]

Al planteamiento sensualista que hace Feyerabend en este texto, la crítica de Zubiri (en ese hipotético diálogo) consistirá en defender las siguientes tesis:

1. Que la búsqueda de la profundidad no es un "sueño filosófico" sino, por el contrario, es una necesidad intelectiva sentida. Con sus palabras:

"no se piensa en el allende por un capricho arbitrario. Porque no es que se inteligen las cosas o aspectos que están fuera del campo "además" de haber inteligido las cosas campales. No es, pues, que haya una intelección aquende el campo y además otra allende el campo. Por el contrario se piensa en la realidad allende precisa y formalmente porque las cosas que están en el campo son ellas mismas las que "dan que pensar". Y este dar que pensar es, por un lado estar llevados a inteligir lo allende, pero por otro consisten en estar llevados a lo allende por la fuerza inexorable de la intelección de lo que está aquende"[69] .

2. Que la profundidad no es "un segundo mundo oculto", (con las connotaciones de "misteriosa raíz", y "hondura indiscernible"), como afirma Feyerabend y todas las concepciones positivistas. La aportación de Zubiri a esta cuestión estriba en la diferencia que establece entre realidad campal y realidad mundanal o "trans-campal" o "allende" o "en profundidad" (son sinónimos). Para Zubiri, la matemática (como cualquier otra intelección racional) es una determinada intelección de lo real en profundidad. Lo que no está en el campo es inteligido para poder inteligir mejor lo que está en él... es la intelección en el "por" sentido. Ir a lo allende es ir al fondo de las cosas reales. Y este fondo es justo la razón de ellas. Sólo inteligiendo este fondo habremos inteligido las cosas reales del campo. En las cosas físicas esto está claro, pero ¿cómo se aplica esto a la matemática?

Dice Zubiri, refiriéndose en concreto al espacio, que el espacio perceptivo o campal no es lo mismo que el espacio actualizado en su realidad profunda; la realidad es la misma, su actualización tiene distinto contenido. Este contenido de la realidad profunda del espacio perceptivo o campal es libremente postulado y depende de las distintas geometrías.

"El espacio campal, el espacio perceptivo, es espacio pregeométrico. Pues bien, se postula que este espacio campal tiene en su realidad profunda determinados caracteres intrínsecos sumamente precisos".[70]

Y, un poco más adelante, añade:

"El espacio geométrico es por esto fundamento profundo del espacio pre-geométrico"[71]

El sensualismo que Feyerabend defiende a propósito de Aristóteles se apoya totalmente en el sentido común, que se presenta no como una ilusión sino como algo seguro en el que podemos confiar y que no necesita ser sustituido por un análisis "más profundo". Por tanto, la autoridad o criterio de verdad se reduce a la percepción no distorsionada. Pero según Zubiri la percepción no sólo nos ofrece las cualidades sensibles sino también la formalidad de realidad. La realidad campal es lo sentido de la realidad mundanal, pero queda en pié buscar qué sea la realidad en cuanto realidad, a la que nos vemos lanzados por el campo mismo de la realidad, por ser idéntica la formalidad de realidad en el campo y en el mundo.

En el sensismo no se trata de identidad del contenido mundanal y campal (por ejemplo, que el espacio mundanal tuviese un contenido idéntico al espacio campal) sino de la mismidad de la formalidad de realidad de la realidad mundanal y la realidad campal (siguiendo el ejemplo, que la realidad del espacio geométrico sea la realidad del espacio pre-geométrico o espacio campal). Para Zubiri, en la intelección matemática no hay un aumento de realidad a partir de la dada en la aprehensión primordial —esto es lo que significa el sensismo—, sin embargo, hay un aumento de su contenido en profundidad — y en esto se opone al sensualismo—. De otra manera el esfuerzo de la matemática y de la ciencia sería inútil. Pero, insistimos, el aumento del contenido (que es postulado en la realidad campal) sólo es posible porque sentimos la formalidad de realidad.

"las geometrías son postulación: la intelección de la realidad profunda del espacio es por tanto libre creación"[72]

Así como el sensualismo excluye e imposibilita el racionalismo concipiente en la matemática; el sensismo exige y posibilita el racionalismo sentiente de la matemática.

 

2.4. Intelección constructiva de los conceptos matemáticos

La construcción matemática, nos dice Zubiri, es realización "según conceptos". Y esta realización es una postulación constructiva "según conceptos". El tomar esta expresión aislada puede inducirnos al equívoco de pensar que esta construcción por postulados es la primera construcción que nuestra inteligencia hace; esto sería así en el caso de que dispusiéramos de unos conceptos a priori o los obtuviésemos por mera abstracción de las cosas, pero no es el caso ni de lo uno ni de lo otro. El matemático tendrá que comenzar "haciendo" sus conceptos. Así como Zubiri es explícito en la construcción de los objetos matemáticos, no lo es, sin embargo, en la de los conceptos matemáticos. Es preciso, pues, explicitar en el campo de la matemática, como paso previo a la construcción de los objetos matemáticos, la intelección constructiva de los conceptos matemáticos.

En primer lugar, observamos que el sentido de concepto no tiene en este autor el usual desde la perspectiva de inteligencia concipiente. Una vez más tenemos que recordar la tesis fundamental de Zubiri que afirma que la inteligencia concipiente está constitutivamente fundada en inteligencia sentiente. Hay que situarse, pues, en la perspectiva de inteligencia sentiente para elaborar los conceptos de la Matemática. Los conceptos matemáticos frente a la tradición lógico-formal, nos dice Zubiri, no son conceptos lógicos.

"Son necesarios los conceptos, pero han de ser conceptos de inteligencia sentiente y no conceptos de inteligencia concipiente"[73]

Los referentes de los conceptos sentientes son primariamente "realidades en concepto" a diferencia de los referentes de los conceptos lógicos que son contenidos objetivos. Zubiri lleva a cabo el giro desde la intelección lógica del concepto a la intelección constructiva sentiente del concepto [74].

"Concepto no es algo primariamente lógico sino real: es el ‘qué-concepto’. El concepto envuelve formalmente y físicamente el momento de realidad. El concepto es ‘la’ realidad física misma como si fuera este ‘qué’: concebimos qué sería realmente la cosa, lo que ésta sería en realidad. El concepto es, pues, la realidad terminada en libre qué". [75]

No se trata de "concepto de realidad" sino de "realidad en concepto"’ algo muy distinto. La raíz de esta distinción está en que desde la inteligencia concipiente nos movemos en conceptos mientras que en la inteligencia sentiente siempre nos movemos, como hemos visto, en "la" realidad dada en impresión. Según Zubiri, la cosa aprehendida en aprehensión primordial tiene un qué (al igual que un "esto" de sus notas, y un "cómo" de la configuración de las mismas), pero se da compactamente con las otras dimensiones. Por un movimiento de distanciamiento de la cosa, "en" su realidad campal, desrrealizamos el contenido concreto de la cosa con lo cual la inteligencia permanece en "la" realidad como ámbito de libre creación de lo irreal y puede proyectar en ella un libre qué: es el concepto. El concepto es término irreal: es lo que la cosa "sería" en realidad (dentro del campo de realidad). El movimiento que desrrealiza el "qué" y lo reduce a mero concepto es un movimiento libre y creador. Pero no es un acto de libertad en el vacío sino que está orientado desde la cosa real aprehendida.

El qué reducido a mero concepto es el ‘sería’ y como tal es término de la simple aprehensión, y, según Zubiri, lo es en dos formas:

a) Es un ‘qué’ abstracto.

La desrrealización de la concepción es abstracción. Zubiri distingue abstracción de extracción. Un extracto no es lo mismo que un abstracto. La extracción lleva a cabo una ‘división’ en partes. El resultado, por tanto, es una ‘cosa-extracta’. La abstracción, por el contrario, no divide una parte de otras sino que al inteligir alguna ‘prescinde’ de otras. Es una ‘precisión’, nos dice, según su etimología de prescindimiento. De este movimiento resulta un ‘abstracto’. Este movimiento precisivo es lo esencial de la abstracción.

Zubiri señala que en la abstracción sólo se apunta el aspecto negativo, y no que la abstracción sea un movimiento, esencialmente positivo y creador: "es la creación del ámbito mismo del ‘abs’ como ámbito de irrealidad", quedamos en la formalidad campal de realidad.

"La forma como ‘la’ realidad termina en un ‘qué’ reducido a concepto, es ser ámbito de ‘abs’’. [76]

El movimiento abstractivo es libremente creador. Porque se hace siempre en una dirección que no viene unívocamente-determinada. El abstracto no es "abstracto de realidad" sino "realidad en abstracción".

b) El "qué-concepto" es constructo.

Conceptos abstractos son el "qué" de realidades concretas, por ejemplo: hombre, animal, piedra... Son "precisiones" de realidades individuales existentes "en y por sí". Pero en el caso de la matemática ¿de qué realidades abs-traemos unas notas prescindiendo de otras para formanos los conceptos matemáticos?. Evidentemente no existen tales realidades, más bien, lo que ocurre es que, a falta de éstas, nuestra inteligencia tiene que construir los conceptos matemáticos, aunque sea apoyándose en conceptos abstractos. En efecto, Zubiri señala que además de conceptos abstractos hay conceptos construidos.

"Pero, en segundo lugar, el "qué-concepto" no es sólo abstracto: es también constructo. Empleo aquí este vocablo no para designar el "estado constructo" sino como vulgar sinónimo de algo construido" [77]

Y continúa diciendo que la mayoría de los conceptos científicos y, nosotros pensamos que muy especificamente los conceptos matemáticos, son mera construcción de la inteligencia. Claro está, de una inteligencia que es sentiente. Explícitamente nos dice que la intelección, en general, de los conceptos científicos es una "intelección constructiva". Esta afirmación tiene un gran alcance en la filosofía de la matemática. El qué-concepto, por el carácter sentiente de la inteligencia, es "realidad en construcción".

"La filosofía usual ha pensado sobre todo en que los conceptos son abstractos, que son algo abstraído de las cosas reales. Lo cual es verdad. Pero la verdad es que la mayoría de los conceptos, sobre todo de los conceptos científicos, no son meramente abstraídos sino que están construidos por la propia inteligencia. La intelección de conceptos es en sí misma intelección constructiva. El ‘qué-concepto’ es la realidad en construcción" [78]

Zubiri no es más explícito en este punto, pero está claro que hay una primera dimensión constructiva sentiente de los conceptos matemáticos. Los conceptos matemáticos son conceptos constructos. El matemático no parte de unos conceptos establecidos lógicamente, por el contrario, el matemático hace sus conceptos, esto es, los construye en "la" realidad campal que nos dan las cosas reales concretas, pero desrrealizada del contenido particular que tengan. Esta construcción conceptiva no es absoluta, se opera sobre las notas abstractas. Y esto es, precisamente, lo que diferencia una construcción de conceptos de una construcción de fictos. Según Zubiri, tanto el ficto como el concepto son maneras de construcción, ahora bien, mientras que el ficto es una reconformación de notas separadas de las cosas reales; el concepto es, sin embargo, el resultado de operar sobre notas abstractas o "prescindidas".

"Ya en el ficto asistimos a una primera manera de construcción: la reconformación de las notas en un ficto. Pero aquí la construcción tiene otro aspecto. Porque no opera sobre notas separadas sino sólo sobre notas "prescindidas", sobre notas abstractas. Con lo cual, el resultado ya no es un ficto sino un concepto, un ‘qué’" [79]

En la construcción físico-matemática, la inteligencia parte de un concepto constructo y a partir de él construye un ficto. Se pone de manifiesto que la construcción del ficto y la del concepto no son forzosamente independientes:

"Yo puedo efectivamente construir un ficto al hilo de un concepto constructo: es por ejemplo, el caso de la construcción físico-matemática"[80]

Estamos acostumbrados a ver, nos dice Zubiri, los conceptos organizados como si estuviera ya lógicamente prefijada su organización. Es una vez más la logificación de la intelección. Así nos encontramos la organización de los conceptos según géneros, diferencias y especies. Cualquier determinación, es, sin embargo, una libre construcción.

Zubiri desde la inteligencia sentiente aporta, pues, una nueva concepción de qué sea concepto. Los conceptos no son formas "a priori" del entendimiento como pensara Kant, sino por el contrario, vienen de la realidad libremente acabada en un "qué". Los conceptos no son conceptos de realidad sino la realidad misma hecha concepto, esto es, "realidad en concepto". La realidad sentida es un momento del concepto en cuanto tal. La realidad tiene primacía sobre el concepto.

 

2.5. Postulación constructiva en "la" realidad física.

2.5.1 Construcción libre (postular)

Acabamos de ver que los conceptos matemáticos son conceptos constructos, los obtenemos por intelección constructiva. Ahora bien, con simples conceptos no tenemos matemática, no constituyen el objeto matemático, porque los conceptos expresan lo que lo real "sería", es decir, se inscriben en "la" realidad en cuanto terminaría en un contenido determinado. Ahora bien, la matemática no trata, dice Zubiri, de cosas que "serían" (irreales), sino de cosas que "son" (reales); no trata de "conceptos objetivos" sino de "cosas que son así"

La cuestión es ¿cómo pasamos del "sería" de los conceptos al "es" de los objetos reales? La respuesta de Zubiri es que lo irreal se realiza por postulación constructiva. De este modo los objetos matemáticos son cosas irreales pero realizadas constructivamente.

"A este terminar "determinado", es a lo que de una manera unitaria llamo, con un vocablo tomado de la matemática, postular. Lo irreal, sin dejar de serlo, cobra realidad postulada. Cuando el modo de realización es construcción entonces tenemos la construcción tanto de lo matemático como de lo ficticio. Las afirmaciones de la matemática y de la literatura de ficción, recaen así sobre un irreal realizado por postulación constructiva, sea en forma de construcción según conceptos (matemática), sea en forma de construcción según perceptos y fictos (literatura de ficción)" [81]

En este caso, la construcción ya no concierne a los conceptos,

"no es una construcción "conceptiva" sino que es una realización en "la" realidad física, pero "según conceptos"; dos cosas completamente distintas". [82]

Los postulados postulan el contenido de "la" realidad y no mera verdad. Por ello, nos dice Zubiri, que no se trata de postulación de realidad sino de realidad en postulación. Ahora bien, Zubiri parece que superpone, con cierta ambigüedad, dos planos de la creación del contenido de la realidad matemática, uno sería la creación del contenido de la realidad campal (la intelección del logos sentiente) y otro sería la creación del contenido de la realidad profunda de la realidad campal (la intelección de la razón sentiente). Lo dicho hasta ahora afecta a la construcción postulativa del contenido de la realidad campal. Y por eso las citas son de Inteligencia y Logos. Nada nos dice aquí sobre la postulación del contenido de realidad profunda, sin embargo, en Inteligencia y Razón nos habla de ésta,

"El modo como lo libremente construido dota intelectivamente a la realidad de contenido propio, no consiste ni en modelación ni en homologación: es radical postulación. La realidad profunda se actualiza en lo libremente construido por postulación. Ya lo expliqué en la Segunda Parte. No se postula verdad sino contenido real."[83]

Y vuelve, insistentemente, a decirnos:

"Postulación es el modo como se dota a la realidad profunda de un contenido libremente construido. La realidad se actualiza en mi libre construcción, la cual se convierte así en contenido de lo real; todo lo libre que se quiera, pero siempre contenido de lo real".[84]

La libre creación racional en la matemática es construcción libre (Postular), que apoyándose en la constructividad de lo campal, dota a la realidad profunda de un contenido completamente creado o construido tanto en las notas como en la estructura. Y, en cuanto libre construcción, la construcción matemática (lo mismo se diría de la literatura de ficción) es el acto de máxima libertad, porque no se trata sólo de libertad respecto a las notas de las cosas campales, ni tampoco sólo de libertad respecto al modo de sistematización o de la estructura básica de las notas, sino que, a la vez, es libertad de las notas y de la estructura; por tanto, se apoya en "la" realidad como campo de libertad del contenido de forma total. Si nuestra libre construcción adopta modelos o estructuras básicas de lo campal, lo adopta libremente. Así, nos dice Zubiri, respecto de la libertad de la construcción,

"Libertad no es tan sólo libertad de modificar notas ni de homologar estructuras; aquí libertad es liberación de todo lo campal para construir el contenido de la realidad profunda. "[85]

Al hablar de libertad no se refiere, Zubiri, a que podamos inteligir como se nos antoje, pero sí a que la respuesta determinante de mi intelección a la imposición de lo real en profundidad es necesariamente libre. De lo que se está libre no es de "la" realidad sino de su contenido determinado. La postulación es el modo como lo libremente construido dota intelectivamente de un contenido propio a la realidad. No se postula, por tanto, verdad sino contenido de lo real. Según Zubiri, todo objeto matemático está construido por postulación. Ésta consiste en dar a la realidad profunda un contenido que libremente hemos construido. No se trata de dar realidad a nuestra libre construcción sino, a la inversa, se trata de dar nuestra libre construcción a la realidad, esto es, de dotarla postuladamente de un contenido. La postulación no es de formalidad de realidad (que nos es dada en aprehensión primordial) sino que es del contenido de la realidad.

"Se postula lo que es "suyo" pero no se postula el "de suyo" mismo."[86]

El término "libre construcción" no debe inducirnos al error de pensar que origina una nueva realidad, esto es, que produce algo que no fuera real hasta entonces. En este sentido, conviene recordar que en inteligencia sentiente nos movemos en la línea de la actualidad y no en la línea de la actividad o producción. De este modo hay que entender lo que es realización: es un modo de actualidad y no de producción de realidad. La realidad, primaria y necesariamente dada, se actualiza en el contenido que libremente he construido y, respectivamente, realizo lo postulado constructivamente como contenido suyo. De estos dos momentos, dirá Zubiri, que el segundo se apoya en el primero.

"Esta realización libre no es producción, sino que es una realización tan sólo en la línea de la actualidad. Realización independiente del campo y sin producción: he aquí la libre construcción."[87]

Desde esta concepción de la Trilogía de la intelección hay que entender lo que al parecer dice Zubiri en su curso inédito sobre El Espacio (1973), según la exposición que hace de algunas de las ideas contenidas en el mismo Antonio Ferraz en su artículo El espacio en la metafísica de Zubiri :

" Las estructuras [del espacio] son de tipo operativo. Pero decir que las estructuras que se consideran en el espacio son operacionales podría inducir el error de considerar que las operaciones son operaciones que ‘tolera’ el espacio, y no se trata de eso. Son operaciones que "producen" las estructuras del espacio. Es el matemático quien determina las condiciones iniciales de un espacio. Son operaciones productivas. Sin duda, lo operado, lo producido —hay que decirlo una vez más— no depende en su verdad de la realidad física de su objeto. ¿Son, entonces, irreales las estructuras geométricas?" [88]

Aquí Zubiri no habla de la matemática como realización por postulación constructiva, sino que la construcción matemática la considera como una serie de operaciones productivas. En los mismos términos lo recoge Ignacio Ellacuría en El espacio, lo que nos asegura que, en efecto, es la expresión utilizada por el propio Zubiri.

"¿Qué son entonces las estructuras del espacio? Son de tipo operacional, pero no de operaciones toleradas por el espacio, sino operaciones productivas?" [89]

Lo que en este curso de 1973 debió expresar Zubiri como operación productiva, pensamos que tiene buen cuidado de no utilizarlo de este modo en su Trilogía de la intelección; la razón posiblemente está en la carga de connotaciones del término producir. "Yo pongo", "yo produzco" son términos expresivos que definen el idealismo filosófico, del que Zubiri cada vez está más lejos. Lo que aquí denomina operación productiva en la Trilogía de la intelección lo denomina realización por postulación constructiva. Sin embargo, nos parece una precisión más terminológica que conceptual, porque Zubiri cuando habla en 1973 de "operaciones productivas" no se refiere a una producción "ex nihilo" del sujeto como la creación de una realidad. La operacionalidad productiva sólo puede entenderse desde la irrealización matemática (como constatan tanto Ignacio Ellacuría como Antonio Ferraz). A. Ferraz recoge la siguiente cita textual de Zubiri, haciendo notar, en efecto, su importancia capital,

"...el momento de realidad no solamente es un carácter que tiene cada una de las cosas, sino que es una especie de ámbito en que la inteligencia queda, precisamente porque es más que aquello en que la cosa real consiste; porque excede o transciende físicamente a lo que es cada una de las cosas. La realidad como ámbito es el momento de realidad en cierto modo tomado en su transcendentalidad, respecto de las cosas reales que hay en la realidad"[90]

El ámbito de realidad es el que posibilita la libre construcción que hace la inteligencia de un contenido de "la" realidad en que ya está y se mueve. Esto mismo recoge Ignacio Ellacuría,

"Los objetos matemáticos son determinaciones construidas dentro del momento "físico" de realidad y precisamente por el momento de realidad como ámbito" [91]

En estos términos se expresa, Zubiri, en Inteligencia y Logos. Considera que la inteligencia se mueve en el ámbito de realidad (por la dimensión campal de la formalidad de realidad, que excede de la dimensión individual), esto le permite moverse con libertad respecto al contenido concreto de las cosas reales. En esto consiste la irrealización. La realidad como ámbito es condición de posibilidad para que el matemático construya sus objetos.

Nos encontramos a esta altura con la dificultad de si en las realidades matemáticas, como en las realidades de las ciencias naturales, "lo libremente construido queda realizado en la realidad-fundamento como contenido fundamentante de la cosa campal" Y si es así, ¿de qué realidad campal? , y la dificultad está en que hemos dicho que no hay aprehensión primordial de las realidades matemáticas.

Desde luego, no hay duda de que Zubiri lo aplica igualmente a lo matemático,

"Pero lo libremente construido puede quedar realizado en la ‘realidad-fundamento’ como contenido fundamentante de la cosa campal. Entonces lo libremente construido es contenido ‘fundamental’: es la postulación teorética"[92]

Y es que, a continuación, nos va a poner como ejemplo "especialmente grave y decisivo" de postulación teorética la geometría.

"No es difícil poner algunos ejemplos de postulación especialmente graves y decisivos. Ante todo, la intelección racional de la realidad espacial del campo perceptivo en su realidad profunda: es la geometría". Toda geometría consiste en un libre sistema de postulados (incluyendo en ellos los llamados axiomas). En la geometría se postula libremente que la realidad profunda del espacio campal tiene determinados caracteres precisos: es el espacio geométrico" [93]

En el caso de la geometría, partimos de una realidad campal: el espacio campal o espacio perceptivo (como tal no es un objeto geométrico sino pre-geométrico) y postulamos constructivamente el contenido de su realidad profunda o fundamentante, esto es, el espacio geométrico. Analizamos seguidamente las geometrías como ejemplo crucial de la postulación constructivo-sentiente en la matemática.

 

2.5.2 Las geometrías: postulación constructiva teorética

La creación de las geometrías[94] no euclídeas en el s. XIX tuvo una profunda repercusión en la comprensión de la naturaleza de las matemáticas y su relación con la realidad física. Originó problemas en el área de fundamentación de la matemática, propiciando el abandono de la intuición y su sustitución por el método lógico. La geometría vendría a ser la constitución de sistemas de axiomas y postulados libremente creados, a partir de los cuales se deduciría lógicamente todos los teoremas geométricos, es la postura del logicismo de Russell y del formalismo de Hilbert. Esta es también la concepción del primer Zubiri. Sin embargo, el Teorema de Gödel conmociona estas "escuelas" filosóficas de la matemática, y exige una nueva interpretación. Zubiri ofrece una interpretación constructivo-sentiente de la geometría.

Toda geometría, nos dice el autor, es una libre construcción y postulación teorética. La libre construcción es el acto de máxima libertad, porque no se trata sólo de libertad respecto a las notas de las cosas campales —esto es modelizar—, ni tampoco sólo de libertad respecto al modo de sistematización, o de la estructura básica de las notas, sino que, a la vez, es libertad de las notas y de la estructura, así, pues, es campo de libertad del contenido de forma total. La postulación es el modo cómo lo libremente construido dota intelectivamente de un contenido propio a la realidad. No se postula, por tanto, verdad sino contenido real. La geometría en singular no existe, no es una ciencia de un espacio único, físico o intuitivo. Por el contrario,

"las geometrías son postulación; la intelección de la realidad profunda del espacio es por tanto libre creación"[95]

Las geometrías consisten en un libre sistema de postulados que determinan el contenido de la realidad profunda del espacio campal, esto es, del espacio geométrico.

"El espacio campal, el espacio perceptivo, es espacio pregeométrico. Pues bien, se postula que este espacio campal tiene en su realidad profunda determinados caracteres intrínsecos sumamente precisos" [96]

El espacio pre-geométrico no es idéntico al espacio geométrico, la realidad es la misma, su actualización tiene distinto contenido. En la actualización campal el espacio es el espacio perceptivo, pero la actualización mundanal o realidad-profunda es libre construcción, y según las distintas geometrías tiene diferentes contenidos. El hecho de que existan geometrías con distintos postulados libremente elegidos muestra que al espacio geométrico le compete la posibilidad de distintos contenidos; cada una de estas posibilidades es un espacio determinado. El espacio geométrico es construido libremente dentro del ámbito de realidad.

Esta diversidad de sistemas de postulados, según Zubiri, muestra dos cosas:

1. Que el espacio geométrico y el espacio perceptivo, siendo los dos espacios, son, sin embargo, distintos. El espacio geométrico es fundamento libremente construido del espacio perceptivo.

"no es espacio absoluto —sería absurdo— pero tampoco es aún un espacio geométrico. Por esto lo llamo espacio pre-geométrico. Es un espacio que no posee caracteres rigurosamente concebidos, porque el concebirlos hace ya que este espacio pre-geométrico se torne en espacio geométrico. El espacio geométrico es por esto fundamento profundo del espacio pre-geométrico"[97]

El desarrollo de las matemáticas nos muestra que se han construido varios sistemas de geometría que son incompatibles con la geometría euclídea y en los cuales, por ejemplo, no son adecuadas las proposiciones de que por dos puntos sólo pase una recta, o que la suma de los ángulos de un triángulo es igual a dos rectos. Esto nos muestra que son libre construcción tanto el espacio euclidiano, como el espacio hiperbólico (Lobatchevski y Bolyai) y el espacio elíptico (Riemann).

"La diversidad de postulados muestra, pues, ante todo que ambos espacios son efectivamente espacio, pero que el espacio pre-geométrico es distinto del geométrico. En especial, nos muestra de esta manera que el propio espacio euclidiano no es, como suele decirse tantas veces intuitivo, esto es, nos muestra que el espacio euclidiano es una libre creación de espacio geométrico".[98]

2. Al ser distintos, e incluso independientes, los sistemas de postulados del espacio geométrico, según Zubiri, nos muestran la diversidad de aspectos estructurales de éste, que son incluso separables: conjunción, dirección y distancia.

"Topología, afinidad, métrica, tanto en toda su independencia como en su posible unidad condicional en algunos casos, así como la independencia de las estructuras postulables dentro de cada una de aquellas geometrías, todo ello muestra que la intrínseca inteligibilidad racional de la realidad profunda del espacio acontece en una libre construcción" [99]

La geometría es libre construcción, libre creación, pero no de verdades sino del contenido de la realidad profunda del espacio. Por ello es preciso insistir en la idea de Zubiri de que la construcción de las geometrías es sentiente y no meramente lógica. Zubiri opone su concepción a la meramente logicista que, por ejemplo, representa Hans Hahn, quien nos dice:

"El hecho es que toda geometría tridimensional tanto como multidimensional, euclídea tanto como no-euclídea, arquimediana tanto como no arquimediana, es una construcción lógica" [100]

Zubiri considera el espacio como una construcción, ahora bien una construcción que es sentiente no una construcción que es lógica. No debe inducirnos a error el encontrar en Zubiri expresiones como la que transcribimos a continuación.

"...el espacio intuitivo no es euclidiano, sino que deja abierta la interpretación euclidiana o no euclidiana de su estructura. La geometría euclidiana no es ni más ni menos creación conceptual que todas las geometrías no-euclidianas. Es, a lo sumo, una conceptuación, en cierto modo más ‘natural’[101]

En la Trilogía de la intelección, Zubiri tiene buen cuidado de no utilizar el término "conceptuación" sino el de "realización" "según conceptos", posiblemente para evitar una interpretación logicista como la defendida,por ejemplo, por Hans Hahn y, en general, por los miembros del Círculo de Viena y el Positivismo lógico.

 

2.5.3 Apoyo campal para la libre construcción matemática: la constructividad.

Es importante llamar la atención sobre un texto en el que Zubiri apunta que la constructividad es el aspecto de lo campal en que se apoya la libre construcción, tipo de libre creación racional que se da en la matemática, para dotar de un contenido postulado a la realidad profunda de lo campal. Y lo decimos con esta fuerza porque nos parece un aspecto de una importancia capital y que, sin embargo, como tal, no lo hemos visto mencionado en ningún otro lugar. El texto es el siguiente:

"Recapitulemos lo dicho. Nos preguntábamos cuáles son los modos de libre creación racional. Hemos visto que son especialmente tres. Se apoyan en tres aspectos de lo campal: la experiencia de notas, la estructura, la constructividad. En estos tres aspectos se despliega la creación de carácter libre: experiencia libre, sistematización libre, construcción libre. Por la experiencia libre se dota a la realidad profunda de un contenido modélico. Para la sistematización libre se dota a la realidad profunda de estructura básica. Por la libre construcción se dota a la realidad profunda de contenido completamente creado. (...) Modelizar, homologar, postular: he aquí los tres modos de creación racional"[102]

Esquemáticamente

Aspectos de apoyo campal	Creación de carácter libre	Modo de dotar a la realidad profunda de un contenido
experiencia de notas	experiencia libre	modelizar (contenido de modificar determinada notas campales
estructura	sistemazación libre	homologar (contenido de estructura básica)
constructividad	construcción libre	postular (contenido completamente (construido)

 

¿Qué quiere decir Zubiri con constructividad? ¿significa sólo contenido completamente construido? Nos parece que hay una ambigüedad en este punto. La primera columna nos sugiere que lo campal tiene tres aspectos distintos: notas, estructura y constructividad. Así la constructividad parece un aspecto de la realidad campal. Sin embargo, la tercera columna nos sugiere que constructividad es construcción total de notas y estructura. Desde luego, tiene que ser construcción total, porque cada grado superior, por decirlo así, de libertad supone los anteriores. Así, la libertad de la sistematización libre además de la libertad de la estructura de lo real determinado supone también la libertad de sus notas (que se da en la experiencia libre) para dotar a la realidad profunda de lo real concreto de un contenido libremente creado; su apoyo está en algún tipo de estructura de lo campal, de tal modo que pueda homologarse a la que trata de inteligir la razón. "Lo que hacemos, dice Zubiri, es considerar que la estructura básica de lo real profundo es de la misma índole que la estructura básica de tales o cuales cosas campales"[103] Pues bien, en el grado de máxima libertad, esto es, en la libre construcción, estamos libres tanto de las notas como de las estructuras de todo lo campal, a diferencia de los tipos anteriores que hemos visto que se apoyan en alguna de éstas.

"Pero hay un paso más y muy radical de libertad. Consiste en que el ámbito es campo de libertad para construir completamente su contenido construyendo a la vez notas y estructura básica. Entonces la intelección racional puede dotar a la realidad profunda de este contenido libremente construido" [104]

No hay apoyo en estructura alguna de lo campal para la libre construcción, por eso decimos libertad total del contenido de lo campal (de sus notas y de sus estructuras). ¿Pero en qué nos apoyamos entonces para la libre construcción? Volviendo a la cuestión que nos ocupa, y atendiendo a las propias palabras de Zubiri, ¿qué significa que la constructividad es apoyo campal para crear, en libre construcción por postulación, un contenido a la realidad profunda?. Hemos dicho que esta cuestión no está aparentemente, por lo menos, nada clara en Zubiri porque al encontrarnos textos que indican que la libertad de la construcción es liberación total de lo campal, se nos desdibuja algún posible apoyo en la realidad campal.

"...aquí libertad es liberación de todo lo campal para construir el contenido de la realidad profunda"[105]

Un poco más adelante, nos dice Zubiri,

"...me apoyo en el contenido de lo campal tan sólo para dar el brinco de liberación de dicho contenido. Aunque mi libre construcción adopte modelos o estructuras básicas tomadas de lo campal, sin embargo la libre construcción no está formalmente constituida por esto que adopta; si lo adopta, lo adopta libremente"[106]

Cuando Zubiri explica la libre construcción nada dice de la constructividad y, en cambio, aparece mencionada en la recapitulación que ofrece de todo lo dicho respecto a las tres formas de creación racional. Esto puede resultar desconcertante. Nos vemos impelidos a buscar alguna luz sobre esta cuestión, la construcción libre se apoya en la constructividad, al hilo del análisis que Zubiri hace del término constructividad. Constructividad talitativa de lo real es la estructura de "en"-"de", la unidad de lo real se da "en" las notas, y las notas son notas-"de" la unidad de lo real, son la proyección de ésta. Y la constructividad metafísica de lo real es la estructura de "interioridad-exterioridad". Ninguna cosa real, nos dice Zubiri, es acoplamiento ni conexión externa de notas sino que es constructo.

"Efectivamente, el ser nota-de confiere precisamente al sistema un carácter que, formalmente, yo llamaría constructo. Es constructo, digo, donde constructo significa no que a una nota se le van agregando otras sino que cada nota no es lo que es sino siendo precisa y formalmente de las demás, y refiriéndose a ellas"[107]

Del mismo modo que los objetos matemáticos no son reales "en y por sí mismos", habrá que decir que los objetos matemáticos no son constructos "en y por sí mismos"; esto puede llevarnos a pensar que cada uno de los objetos matemáticos se construye por libre postulación independiente del resto. Y esto no es así. La definición y postulación de cada uno de los objetos matemáticos no es independiente del resto ya definido y postulado, sino que tiene que hacerse desde el conjunto de todos ellos. Por ejemplo, esa figura o ese número sólo son tal cual son a partir del conjunto en que se define. Tiene primacía, pues, el "conjunto total definido y postulado" sobre el objeto particular.

"Porque esas "cosas" no son lo que son por ser definidas y postuladas aisladamente cada una de por sí independientemente de otras, sino por ser cada una de ellas lo que es dentro de la definición y postulado que estructura el conjunto entero a que pertenece. Esto es esencial. Ningún "ente" matemático es lo que es sino dentro de un conjunto total definido y postulado, y sólo por referencia a éste tiene sentido la aprehensión de cada uno de los entes matemáticos en cuestión. Cada cosa no es sino un "aspecto" de esta totalidad, es una realización aspectual de lo definido y postulado" [108]

Entre los objetos matemáticos hay unidad de respectividad porque no se constituyen los objetos matemáticos por mera adición, todo lo contrario. Según Zubiri, cada "cosa" matemática no es "de suyo", es decir, no tiene por sí misma realidad propia; sólo el conjunto entero matemático (campo de números, campo espacial...) es "de suyo". Cada cosa matemática tiene realidad como "nota-de" una unidad, como momento del "de suyo" entero. Sólo el conjunto entero tiene sustantividad. Así pues, podemos decir que el orbe matemático tiene carácter sistemático. El conjunto no es mero conjunto de tal modo que, por ejemplo, las figuras fuesen figuras en un espacio. No. Cada nota tiene una "posición" muy determinada en el conjunto. De este modo por ejemplo, una figura es figura de un espacio. Todo elemento geométrico o numérico es un momento constructo "de" el campo espacial o de un campo numérico. Es lo que Zubiri denomina estado constructo. El campo espacial o el campo de números más que conjunto se ve, pues, que es "unidad posicional y constructa de sus notas": es lo que Zubiri denomina sistema. Por eso continúa diciendo Zubiri:

"El orbe matemático no es una yuxtaposición de entes matemáticos definidos y postulados cada uno en y por sí mismo sino que cada uno de estos entes sólo tiene entidad dentro del conjunto total y como momento de él: así, cada figura es figura de un espacio, etc., cada número pertenece a un campo de números, etc. Sólo de este carácter aspectual recibe su realidad cada "cosa" matemática".[109]

Así llegamos a la conclusión de que la constructividad es la construcción que recae sobre el momento del "de". En los textos publicados de Zubiri no encontramos desarrollado este aspecto de la irrealización del "de" de lo real que es la base de la construcción matemática. En el curso de Zubiri sobre El Espacio aparece tratada (no sabemos con qué extensión) esta cuestión; así lo recogen Ignacio Ellacuría y Antonio Ferraz, en sus citados artículos.

"Esta irrealización [matemática] versa formalmente sobre el "de", en que consiste el carácter de sistema, que es propio de toda cosa real. La matemática, en tanto que es construcción afecta formalmente al "de" según tres momentos característicos: es conjunción según un dentro y un fuera, construida libremente por el sujeto humano, y construida según conceptos"[110]

Y

"Toda nota es nota-de, y como ese "de" es el que expresa la sustantividad real de cada cosa, la irrealización consiste en conservarlo como momento de realidad, pero liberado de aquello que es "de" en lo dado. La ficción y la conceptuación recaen sobre el "de" (...)

¿En qué consiste la irrealización propia del "de" que constituye la realidad matemática? Para Zubiri la respuesta a esta pregunta es sumamente sencilla: las operaciones matemáticas, en general, son "construcciones". La construcción es ante todo "conjunción".... construir es siempre "yo construyo". Los puntos del espacio no están unos junto a otros, sino que yo los pongo. Tienen la unidad que les otorgo."[111]

No podemos pasar por alto el doble sentido con el que Zubiri (también nosotros) utiliza el término "constructividad"; por un lado, tiene el sentido de libre construcción y, por otro lado, tiene este sentido de "estado constructo". En esta acepción segunda, Zubiri apela a la noción gramatical de "constructo" que se da en algunas lenguas semíticas (por ejemplo el árabe y el hebreo), alude a la respectividad interna de las notas de un sistema, es decir, al carácter de estar cada nota "vertida" a las demás, de ser "nota-de". Creemos que no son , sin embargo, independientes estos dos sentidos en Zubiri; más aún, uniéndolos podría decirse que la matemática es construcción constructiva. Con esta luz puede verse la afirmación de Zubiri de que para la libre construcción matemática (lo mismo sería para la literaria) nos apoyamos en la constructividad de lo campal.

Al definir la postura de Zubiri en la filosofía de la matemática como constructivismo sentiente, tenemos en cuenta la constructividad como lo construido y la constructividad como el modo constructo de quedar construido el contenido de "la" realidad. Según nuestra interpretación, lo que hemos denominado constructivismo sentiente encierra las dos dimensiones de la filosofía matemática: la dimensión epistemológica (libre construcción) y la dimensión ontológica (la constructividad).

 

2.5.4 Lo racional de la creación matemática: la unidad coherencial propia.

Hemos hablado de la libre creación del contenido de lo matemático, pero si esto es meramente así, ¿cuál es la diferencia con una pura creación irracional?, lo que nos lleva a preguntarnos ¿en qué consiste lo racional de la creación? A ello responde Zubiri diciendo que lo racional de la creación consiste en la unidad propia de lo creado. Distingue varios tipos de unidad: conceptual, metafórica, etc. La creación matemática tiene la unidad de lo conceptual. Lo racional de la creación es la estructuralidad o unidad fundamental. Al realizar esta unidad creada por nosotros, y por tanto concebida, pasa a ser la estructura real profunda de lo real determinado.

"Lo racional de esta creación consiste en ser creación en y de unidad fundamental’. Al ser realizada, esta unidad creada por mí cobra el carácter de estructura real profunda"[112]

Así el sistema de postulados y axiomas del espacio de Hilbert al realizarlo se torna en un espacio de Hilbert. Su unidad estructural es la razón fundamental. No todos los tipos de estructura tienen el mismo grado de unidad. La estructuralidad de máxima unidad la constituye el sistema constructo, en que cada nota sólo tiene realidad como nota-de las demás.

"Hay un tipo de unidad estructural que desempeña una función decisiva: es la unidad estructural que consiste en ser un sistema "constructo", esto es, un sistema en que cada una de sus notas no tiene realidad propia de nota más que siendo intrínseca y formalmente "de" las demás. El ser sistema constructo es la esencia misma de lo real en cuanto real. De ahí su función radical".[113]

Y en Sobre la esencia, dice Zubiri:

"Esta constructividad intrínseca de la esencia como sistema se expresa en dos momentos: la esencia tiene unas notas en estado constructo, esto es, como "notas-de", y estas notas tienen una unidad que es el momento absoluto "en" ellas. (...) De suerte que la esencia como realidad en sistema es una realidad intrínsecamente construida según dos momentos: el "de" de las notas y el "en" de la unidad’ (...) El "de" está construido según el "en": he aquí la constructividad intrínseca de la realidad esencial"[114]

En el punto anterior hemos señalado que los objetos matemáticos se definen dentro del conjunto de entes matemáticos y sólo como elementos-de ese conjunto. Esta unidad del conjunto es primaria, no es un agregado de elementos, y constituye unidad constructa de notas, que por su carácter constructo son co-herentes entre sí. Ahora bien, ¿cómo constituimos intelectivamente la unidad coherencial propia de un objeto matemático, por ejemplo, el espacio de Hilbert?. Zubiri señala que hay varias formas de constituir la unidad intelectiva estructural de las notas, uno de ellos sería la definición, pero ni mucho menos el único; señala otro modo que es de suma importancia para la matemática y consiste en un sistema de axiomas y postulados.

"Aquel sistema de notas ha de tener intelectivamente una unidad coherencial propia. Y esta unidad puede establecerse de muchas maneras. La unidad intelectiva estructural de las notas puede consistir, por ejemplo, en ser definición. No es necesario sin embargo que sea así. Puede ser un sistema de axiomas y postulados. Este sistema de axiomas y postulados no es un mero sistema de definiciones. Lo único que constituye esta unidad intelectiva en cuanto estructural es ser unidad "constructa".[115]

Zubiri considera que la definición es un logos predicativo, y dado que esta función de predicación no es lo primario sino que antes del juicio predicativo hay un juicio proposicional, que lo considera el logos nominal (y antes que éste tendríamos el juicio posicional, pero no es relevante para esta cuestión). Hay una gran diferencia entre el logos predicativo y el logos proposicional que es preciso tener en cuenta para ver la mayor adecuación de este segundo a la construcción matemática. El juicio proposicional, nos dice Zubiri, es ante-predicativo. Entre los dos términos del juicio, A y B, hay una unidad de complexión AB, es decir, lo que B afirma de A pertenece intrínsecamente a A, se funda en la propia índole constitucional de A en cuanto aprehendida, y , por último, es un momento de la realidad de A. Se afirma la unidad complexiva "AB". "Como afirmación, consiste en poner en "la" realidad la unidad complexiva". Para ilustrar cómo nos parece que se aplica esto a la matemática, pongamos un ejemplo. En todos los libros de geometría elemental se nos enseñaba: " la recta, línea que tiene todos sus puntos en la misma dirección"; no se trata de una predicación o atribución copulativa de algo que es A, no, lo que se pone de la recta es su propia constitución. La diferencia a la que nos referimos entre el juicio proposicional y el juicio predicativo radica en que en éste lo que se predica, B, no se funda en la índole misma de A, sino que meramente "está" en A, pero siendo de algún modo distinto de A; por eso, Zubiri llama a esta unidad del juicio predicativo: unidad de conexión.

"Hay una gran diferencia entre complexión y conexión. La conexión es tanto unión como distinción. Unión y separación son los dos aspectos de la unidad de conexión. Esta conexión puede ser de muy distinto carácter: puede ser necesaria o ser sólo de hecho. Pero siempre se trata de una conexión "derivada" de la realidad de A. En cambio, en la unidad de complexión más que de una "necesidad de A", se trataba de la "índole" misma de A. La complexión es por esto más que necesaria, es en cierto modo constituyente"[116].

Volviendo a nuestro ejemplo, al decir "la recta, línea que tiene todos sus puntos en la misma dirección" se afirma que la recta es la línea que tiene todos sus puntos en la misma dirección por ser recta. Pero si dijéramos "la recta es la línea que tiene todos sus puntos en la misma dirección" no afirmaríamos que la recta consiste en tener todos sus puntos en la misma dirección. En este caso la recta sería de índole independiente a tener todos sus puntos en la misma dirección, y sólo habría unidad conectiva o copulativa. Se ve inmediatamente la conveniencia del logos nominal o proposicional para establecer los postulados matemáticos.

Al logos nominal que afirma las notas de lo real en estado constructo, lo denomina Zubiri logos nominal constructo. Aunque Zubiri no lo dice explícitamente, creemos que este autor está considerando también el logos nominal constructo órganon conceptual adecuado para construir las unidades fundamentales de los sistemas de caracteres postulados de lo real matemático (además de las cosas físicas)

"La unidad coherencial intelectiva de lo real en profundidad es la unidad intelectiva en un logos nominal constructo, esto es, en un logos nominal que afirma las notas en estado constructo. Cuando el logos recae sobre notas presuntivamente últimas e irreductibles, tenemos el logos radical de la realidad profunda. Esta unidad es libremente creada" [117]

Y en Sobre la Esencia dice Zubiri en términos similares:

"He aquí, pues, el órganon conceptual adecuado que buscábamos para nuestro problema: el logos nominal constructo. La esencia no puede conceptuarse ni en función de la sustancia o sujeto absoluto, ni en función de la definición, ni en función relacional, sino en función de la "constructividad" intrínseca. La esencia constitutiva, en efecto, es un sistema de notas, y este sistema no es una concatenación aditiva o flexiva de notas, sino que es un sistema de notas intrínsecamente constructo"[118].

Si creamos a través de un sistema de axiomas y postulados la unidad coherencial ¿cómo podemos pretender que sea unidad real?. En efecto, Zubiri afirma que en cuanto creada es "una unidad coherencial meramente intelectiva".

"La actualización de la realidad profunda física en esta unidad confiere a esta unidad el carácter de contenido de aquella realidad profunda. Y a su vez la unidad coherencial intelectiva se ha realizado en la realidad profunda. En su virtud, la unidad coherencial intelectiva ha cobrado el carácter de unidad coherencial primaria de lo real: es esencial. Esencia es el principio estructural de la sustantividad de lo real...La esencia es lo que en este caso ha buscado la razón". [119]

La unidad primaria o unidad esencial es la unidad coherencial. Ahora bien, podemos pensar que unidad coherencial es lo que lógicamente se denomina consistencia o coherencia lógica. La coherencia es un momento de la realidad física, es la estructura según la cual, cada nota está intrínsecamente vertida a las demás "desde sí misma". "Este ‘desde sí misma’ es, formalmente, la unidad coherencial. Por tanto, la razón formal de la unidad esencial es la coherencia" [120] Y añade Zubiri, que esta versión de las notas "desde sí mismas" a las demás se da "de antemano". Por eso es unidad "primaria".

Por todo lo que llevamos dicho en este punto se pone de manifiesto el cambio de marco conceptual de Zubiri respecto de la tradición filosófica griega. La realidad matemática (como toda realidad) no es sustancia sino sustantividad, no es sujeto sino estructura; y la esencia no es el carácter específico (de la especie) del sujeto, sino la constructividad de la sustantividad, esto es, el sub-sistema de notas constructo que determina la posición de todas las demás notas del sistema. En efecto, el sistema de axiomas y postulados matemáticos definen la constructividad, si un postulado se cambia por otro cambia también el objeto matemático en cuestión. Esto es lo que nos muestra la pluralidad de geometrías no-euclídeas. El sistema de postulados y axiomas tal y como los establece Euclides constituyen el espacio euclideano. La sustitución del axioma de las paralelas por otros axiomas distintos constituye espacios no-euclídeos, puesto que el cambio de un axioma constituyente modifica el sistema entero, precisamente por el carácter constructo en que todas las notas se co-determinan.

La física matemática, aunque no sea a través de axiomas y postulados, describe la realidad de los cuerpos y de sus leyes a través de descripciones también no-predicativas. Éstas son descripciones meramente funcionales, estructurales.

 

2.5.5 ¿Es la matemática una construcción como la literatura de ficción?

La matemática, según hemos visto, es esencialmente libre creación de un contenido fundamental en "la" realidad. Ahora bien, nos preguntamos ¿ esta creación es del mismo tipo que la creación literaria de ficción?. Por ejemplo: El personaje D. Juan Tenorio, ¿es de la misma naturaleza que un espacio no-euclídeo o que un número irracional? Resulta provocativa la respuesta afirmativa a esta pregunta, y sin embargo era la sospecha que ya Weyl reflejaba, en l944, cuando mantenía que "el ‘matematizar’ muy bien pudiera ser una actividad creativa del hombre como el lenguaje o la música, de una originalidad primaria, cuyas decisiones históricas desafíen una racionalización objetiva completa". Pero ¿las semejanza de la matemática con la literatura de ficción es una concesión de la racionalidad a la irracionalidad? Esto parece sugerir la afirmación de Weyl.

Zubiri conceptúa la razón sentiente de modo que permite librarse de las reservas que esta afirmación produciría desde una inteligencia concipiente o lógica, porque sería tanto como afirmar que la matemática es irracional. Desde la inteligencia sentiente, en cambio, la libre creatividad de la matemática no la relega al plano de lo irracional; por el contrario, desde la inteligencia sentiente no sólo la matemática es racional, sino que también la literatura de ficción es incluida en el campo racional. Por otra parte, el ámbito tanto de la matemática como de la literatura de ficción es la realidad.

Tan libre construcción es la matemática como lo es la literatura de ficción y en esto no hay ninguna diferencia entre una y otra. La construcción sentiente, tanto en la matemática como en la literatura de ficción, parte de la realidad dada en impresión de realidad de cualquier cosa determinada, por ejemplo de esta hoja de papel, y se construye el contenido por creación en esa realidad en cuanto ámbito (es decir, liberado de un contenido determinado).

Zubiri establece la diferencia entre matemática y novela de ficción del siguiente modo,

"Es toda la diferencia entre novela y matemática. Ambas son construcciones de realidad pero en la matemática se construye "según conceptos", mientras que en la novela se construye "según fictos y perceptos"[121]

En ninguno de los dos casos, matemática y literatura de ficción, se trata de construcción de objetos ideales —éstos serían resultado de una construcción sensible o conceptiva—, sino de realidad en construcción —es el resultado de construcción sentiente. Se construye el contenido determinado de la formalidad de realidad desrrealizada que nos retiene. Los juicios de la matemática y los juicios de la literatura de ficción juzgan sobre "algo real", y no sobre algo "irreal". En palabras de Zubiri,

"Las afirmaciones de la matemática y de la literatura de ficción, recaen así sobre un irreal pero realizado por postulación constructiva, sea en forma de construcción según conceptos (matemática), sea en forma de construcción según perceptos y fictos (literatura de ficción)".[122]

Como ya vimos, aquí se aplican las consecuencias de la interpretación del teorema de Gödel. Al ser lo novelado y lo matemático construcción en la realidad, es por lo que el objeto, "tiene más propiedades que las formalmente enunciadas en un principio"[123]. Lo mismo ocurre en el ámbito de la literatura de ficción. Así nos dice Zubiri, que podemos discutir, a partir de los rasgos que caracterizan según el autor a un personaje de una novela, si tiene o no otras características; por ejemplo, "si ese personaje de ficción que es Don Juan es o no es un personaje afeminado". También de D. Quijote de la Mancha se ha discutido si realmente estaba loco o no. Recordamos que la realidad es "más" que cualquier contenido determinado y ninguno puede agotarla dado su carácter de apertura y de respectividad en cuanto tal realidad.

Zubiri señala una segunda diferencia fundamental entre la construcción literaria, por ejemplo una novela, y la construcción matemática. En la novela se trata de la creación por la creación, esto es, el contenido libremente construido y realizado en "la" realidad por postulación queda reposando sobre sí mismo; por el contrario, en la matemática, en cuanto postulación teorética, no se trata de crear por crear, sino que el contenido libremente construido se realiza en la "realidad profunda" como contenido "fundamental". Al respecto, hemos visto que la geometría consiste en la construcción del contenido de la realidad profunda del espacio del campo perceptivo.

" Lo libremente construido y realizado por postulación puede quedar reposando sobre sí mismo: es la creación por la creación. Es lo propio, por ejemplo, de una novela. Pero lo libremente construido puede quedar realizado en la "realidad-fundamento" como contenido fundamentante de la cosa campal. Entonces lo libremente construido es contenido "fundamental": es la postulación teorética" [124] .

 

2.6 Intelecciónconstructiva del juicio: realización de "B" en "A"

Desde la inteligencia concipiente, el juicio es una relación de conceptos, por el contrario, desde la inteligencia sentiente, juzgar es realizar [125] un concepto, un ficto o un percepto en la realidad concreta ya aprehendida.

"Juzgar no es pues atribuir un concepto a otro sino que es realizar un concepto, un ficto o un percepto en la cosa real ya aprehendida como real en aprehensión primordial".[126]

En el caso de la matemática, no se parte en el juicio de un concepto o sistema de conceptos sino que se parte de una realidad realizada por postulación constructiva. Juzgar es un acto llevado a cabo sentientemente. Se trata de realizar un concepto (construido libremente) en la realidad postulada (constructivamente). En el juicio matemático se afirma lo que lo real postulado es en realidad, en el campo de otras cosas postuladas.

Los términos ‘A’ y ‘B’ de un juicio no son homogéneos sino que hay entre ellos una diferencia esencial: ‘A’ es una realidad postulada y ‘B’ es algo irreal; en la afirmación se realiza el término irreal ‘B’ en la realidad postulada ‘A’. Esta razón hace irreductible el juicio matemático al juicio lógico, porque en éste sí que son homogéneas las dos variables ‘A’ y ‘B’. Zubiri considera la lógica de la afirmación conectiva de la realización de ‘B’ en ‘A’ fundante de la lógica formal. Y no al contrario como defiende el logicismo, en su intento de deducir la matemática de la lógica.

"La ‘lógica formal’ es el juego de dos variables homogéneas. Mientras que la ‘lógica de la afirmación’ es la intelección de la realización de algo irreal (B) en algo ya real (A). Y esto es lo esencial: la lógica de la intelección afirmativa de lo real. (...) no se trata de invalidar la moderna lógica formal sino de fundarla en la lógica de la afirmación". [127]

 

2.7 Método constructivo-sentiente de la matemática.

Constituye un aspecto muy importante de la aportación zubiriana a la filosofía de la matemática su idea de método desde la perspectiva de inteligencia sentiente o sentir intelectivo frente a la idea de método desde la perspectiva de inteligencia concipiente o sentir puro. La filosofía zubiriana de la matemática desde inteligencia sentiente, el constructivismo sentiente, se opone tajantemente a las "escuelas" concipientes de la matemática: el logicismo y el formalismo, lo hemos visto respecto a su concepción de los conceptos, de los sistemas de axiomas y postulados, y de los juicios. Los conceptos matemáticos son "realidades en construcción", que resultan de la intelección constructivo-sentiente; los sistema de axiomas y postulados matemáticos no son verdades lógicas sino contenido de realidad, son construcciones, llevadas a cabo sentientemente, en la realidad. El juicio no es relación de conceptos (ni analítica ni sintética), es construcción sentiente, y como tal es realización de algo "B" en una realidad postulada "A". Pues bien, para completar esta exposición de la nueva filosofía de la matemática de Zubiri, el constructivismo sentiente, tratamos a continuación el carácter constructivo-sentiente del razonamiento matemático, o la deducción constructivo-sentiente de la matemática frente a la deducción lógica.

 

2.7.1 Método lógico-formal versus método constructivo-sentiente

La razón sentiente, según Zubiri, es marcha en la realidad dada impresivamente. Es un error, propio de la vía concipiente, el considerar la razón como marcha lógica en la verdad. Esto es decisivo en su consideración del método matemático (y en general). La caracterización del método constructivo-sentiente de la Matemática la presenta Zubiri en contraste con la caracterización del método lógico-formal de la Matemática. Así lo reflejamos en nuestra exposición.

La primera diferencia fundamental reside, como ya hemos esbozado, en que el método constructivo, en cuanto sentiente, es vía en la realidad, es un abrirse paso en la realidad, mientras que el método lógico formal es vía en la verdad. El método matemático es vía en la impresión de realidad. No se trata de realidad exterior o "allende" la aprehensión, sino de realidad actualizada en la inteligencia,

"...método es una vía en la realidad. El momento de realidad es decisivo. Ciertamente se trata de realidad actualizada, pero actualizada como realidad. El método es un abrirse paso en la realidad misma hacia su más profunda realidad" [128]

Esto es así en la matemática como en el resto de las ciencias. La diferencia está en que mientras en las ciencias físicas, el método es vía en la realidad dada, en el caso de la matemática, el método es vía en la realidad postulada. El método matemático no es razonamiento lógico; si bien está orientado por el rigor lógico, no se reduce a él, sino que lo fundamental es la aprehensión de la realización de algo "B" en la realidad postulada "A".

"El método [matemático] es vía en la realidad postulada, una vía orientada según el rigor lógico. Pero si este rigor demostrativo, por imposible, no llegara a hacernos aprehender la realidad de A como "siendo" B, no tendríamos matemática" [129]

El método es vía desde la actualización campal de lo real a la actualización mundanal de lo real. Método es ir actualizando la realidad. Es vía del objeto real campal a su fundamento mundanal. Por ejemplo, en el caso de la geometría, el método geométrico es la vía que nos lleva desde la actualización del espacio campal a su actualización en el mundo, esto es, al espacio geométrico (según las distintas geometrías). Es insostenible para Zubiri la concepción usual que consiste en considerar el método matemático, y en general, como un razonamiento demostrativo de un juicio —conclusión— a partir de otros juicios —premisas—, según leyes lógicas.

"Usualmente se entiende por método la vía que conduce de una verdad a otra, entendiendo por verdad un juicio verdadero; por tanto el método sería un razonamiento que lleva de un juicio verdadero a otro. Pero esto me parece insostenible..." [130]

Y un poco más adelante, vuelve a insistir en este error que tiene como raíz la logificación de la intelección, y en nuestro caso de la logificación de la matemática.

"La identificación de método con razonamiento, que ha corrido desde hace siglos por todos los libros de lógica es a mi modo de ver insostenible. Se ha caído en ello precisamente por lo que varias veces he llamado en este estudio "logificación de la intelección". Esto es imposible. Ciertamente el método es vía, y a fuer de tal es una vía que ha de ser recorrida; es un discurrir. Pero es un discurrir en sentido etimológico, es un "dis-currir", no es un "discurso", no es un "discurso" lógico."[131]

La esencia de la lógica es el razonamiento deductivo. No se ocupa de la "verdad real" de sus afirmaciones sino de la verdad "lógica", de la corrección de las deducciones. La lógica es la ciencia que estudia las leyes del razonamiento correcto o válido. Pues bien, la logificación de la matemática ha llevado a la identificación de la matemática con la lógica de tal modo que su método también ha quedado unificado: el razonamiento deductivo. La deducción es el proceso mental por el cual derivamos de modo necesario un enunciado de otros, en virtud de las leyes lógicas. La logificación y formalización de la matemática hacen, pues, de ésta una ciencia formal alejándola totalmente de la realidad y de la experiencia. La demarcación logicista de las ciencias establece que la matemática es ciencia formal, en virtud de su método lógico-deductivo, a diferencia de las ciencias empíricas, que siguen un método inductivo.

La obra de Tarski Introducción a la lógica y a la metodología de las ciencias deductivas es claro exponente de la logificación del método matemático. En una teoría matemática se parte de unos términos primitivos, de axiomas o postulados, y a partir de ellos y de los principios lógicos llegamos a los Teoremas; el proceso llevado a cabo es una demostración, derivación o deducción[132]. Sin embargo, esta concepción es errónea para Zubiri. Primero porque se identifica la naturaleza de la matemática con la lógica. Zubiri, por el contrario, según vimos, considera que la matemática no es ciencia formal sino ciencia de realidad, y esta realidad tiene una formalidad dada y un contenido postulado. Precisamente los postulados postulan los caracteres del contenido de "la" realidad. Por tanto, no se puede hablar de la matemática como ciencia que prescinde del contenido de la realidad; mejor aún, se trata de construir el contenido mundanal de la realidad matemática, esto es, de actualizar la realidad mundanal. Y esto no tiene nada que ver con pasar de un enunciado a otro; es irreductible a un discurso lógico-formal. La lógica no es vía en la realidad y por tanto no puede ser el método de las matemáticas, ni de ningún otro conocimiento; sólo puede ser instrumento o órganon. La matemática es saber real porque la razón sentiente marcha en la realidad.

"El método ciertamente ha de conformarse con las leyes estructurales de la intelección lógica. Pero esta conformidad no es ni puede ser método que conduce a un conocimiento, esto es, a una nueva actualización de lo real. Las leyes lógicas, la lógica entera, es órganon del conocimiento, pero no es método "[133]

La deducción, erróneamente considerada como el método de la matemática, es estructura lógica pero no es método. Ya lo hemos dicho, desde el constructivismo sentiente, método sólo es vía en la realidad y no en la verdad. Hay estructura demostrativa en los juicios matemáticos, "pero, nos dice Zubiri, si este rigor demostrativo, por imposible, no llegara a hacernos aprehender la realidad de A como "siendo" B, no tendríamos matemática" [134] Y es que son dos cosas distintas la estructura lógica del pensar matemático y la actualización de lo real matemático.

"La postulación es un modo de realización del contenido, no es un modo de afirmación. En su virtud cuando lógicamente deduzco consecuencias necesarias (incluso consecuencias necesarias y suficientes) de estos postulados, la conclusión tiene dos momentos esencialmente distintos...[el primero] es el momento según el cual la afirmación es una conclusión necesaria de los axiomas, de lo postulado. Pero no es el momento único, hay otro. Y este momento me es esencial destacarlo enérgicamente. Cuando digo en la conclusión que A es B, no enuncio simplemente la verdad de mi afirmación sino que enuncio una propiedad real del objeto matemático" [135]

El logicismo y formalismo, al considerar la deducción lógica como el método adecuado de la matemática, sólo ha tenido en cuenta el primer momento del método matemático, la intelección verdadera, y ha olvidado el segundo momento, el de "la intelección aprehensiva de la realidad matemática como tal". Frente a esta concepción logicista, Zubiri repite, con enorme insistencia y energía, que si obviamos el momento de realidad e identificamos el método de la matemática con la mera deducción lógica, resultará la matemática como "pura lógica de verdades", pero no como saber real. ¡Pero esto es lo que cuestiona precisamente el Teorema de Gödel! Por eso, según Zubiri, hay que afirmar que, además de deducir consecuencias necesarias de los axiomas y postulados, veo en la realidad que realmente es así.

"No sólo logro determinar deductivamente que lo entendido como A tiene que ser B, sino que logro ver que la realidad misma de A está necesariamente siendo B. Si así no fuera, la matemática sería una pura lógica de verdades. Y esto es imposible porque la matemática es ciencia de realidad" [136]

Zubiri considera que para lograr la actualización de lo real matemático no basta con la deducción lógico-formal sino que se requiere la deducción constructivo-sentiente, esto es, "hacer" la deducción en "la" realidad, sólo en este caso tenemos matemática como conocimiento. Para Zubiri la deducción lógico-formal pertenece a la lógica no a la matemática. El matemático, a diferencia del lógico, no sólo deriva sino que esencialmente obra, realiza, sentientemente, en el campo de la realidad. Transcribimos seguidamente el texto de Zubiri que nos parece clave para definir el método matemático dentro del constructivismo sentiente frente al logicismo y formalismo.

"no basta con deducciones rigurosas sino que es menester "hacer" la deducción operando, transformando, construyendo, etc. "en la realidad matemática". Sólo esto es método matemático; no lo es la deducción lógica. Por tanto la deducción por sí misma no es método sino estructura lógica, y además no es método de lo matemático"[137].

Así pues, la diferencia crucial entre el razonamiento lógico-formal y el método constructivo-sentiente de la matemática está en que el primero sólo considera la necesidad lógica, pero ésta en y por sí misma no es la realidad. El método constructivo-sentiente tiene en cuenta tanto el momento de necesidad lógica como el de aprehensión de realidad,

"Ciertamente, son dos momentos de un mismo acto, de un acto único, pero como momentos son distintos. Y en ellos el momento de necesidad lógica no es el primario porque los postulados a su vez no consisten en afirmaciones lógicas sino en postulaciones de contenido de realidad. Es la realidad, pues, la que tiene la primera y la última palabra en toda intelección matemática". [138]

Además de lo dicho anteriormente sobre la deducción no hay que olvidar que en la matemática hay un tipo especial de inducción matemática. Por ejemplo, Gentzen probará por el método de inducción transfinita la completitud de un sistema formal que contenga la aritmética. Zubiri afirma que en el caso de la inducción, la confusión es de signo inverso al señalado en la deducción. La deducción no es método sino estructura lógica o razonamiento; pues bien, la inducción es método pero no es razonamiento o estructura lógica. Esta puede ser la razón de la reserva con la que es acogida la prueba de Gentzen. De ningún modo podemos decir que haya en la matemática razonamiento inductivo. Para que así fuera tendría que formularse el principio de inducción, y esto no ha sido posible.

"lo menos que haría falta es que se enunciara lo que suele llamarse el principio de inducción. Y esto, de hecho, no ha sido logrado jamás satisfactoriamente, ni siquiera al recurrir al cálculo de probabilidades para excluir los errores azarosos de la experimentación. Por tanto, de hecho no existe un razonamiento inductivo. En cambio, la inducción existe como método estricto y riguroso" [139]

La crítica de la filosofía de la ciencia actual a la inducción es a la consideración de ésta como razonamiento, aspecto que Zubiri critica igualmente, sin embargo, como nos dice, queda en pie la inducción como método. Una filosofía sentiente de la matemática no se ocupa, pues, del razonamiento sino que se ocupa del método, como vía en la realidad.

Zubiri no niega lo que es evidente, y es que en la matemática haya razonamientos deductivos, como hay también juicios y conceptos. Lo que pretende es acentuar la otra dimensión del método matemático que no es la estructura lógica —y que por supuesto tiene en cuenta—, sino que es la aprehensión de realidad postulada. El método es más que la estructura lógica, es la actualización de realidad, y esto es lo esencial. En la matemática, pues, el razonamiento deductivo no es método, porque no es vía en la realidad sino en el pensar, y en cuanto tal no es fuente de verdad real.

"En la matemática tenemos un razonamiento deductivo que por sí mismo no es método, en la inducción tenemos un método que por sí mismo no es razonamiento.

Esto no significa que en la intelección racional no haya razonamientos. Los hay y tiene que haberlos forzosamente, de la misma manera que hay juicios. Pretender lo contrario sería más que una imposibilidad una estupidez. Pero ni los juicios ni los razonamientos son lo que formalmente constituyen método"[140]

Y continúa diciendo que la lógica no es fuente de verdad; puede llevarnos a enunciar nuevas proposiciones, pero nunca a actualizar la realidad matemática ni a descubrir nuevas direcciones de marcha intelectiva en la realidad. El método matemático sí, por ser vía en la realidad postulada.

"El razonamiento es una estructura lógica que el método ha de respetar. Pero esto es cuestión de lógica. Y la lógica por sí misma nunca es, ni pretende ser, fuente de verdad. En cambio el método es esencialmente, cuando menos pretende serlo, fuente de verdad puesto que se mueve en la realidad" [141]

El descubrimiento de nuevas verdades es posible porque el método es constructivo-sentiente, sólo en cuanto sentiente nos movemos en la realidad que aprehendemos en aprehensión primordial de realidad. Volvemos a ver toda la dimensión de la afirmación zubiriana de que es preciso sentir lo matemático para poder construir la matemática. El método matemático no es puramente racional ni puramente empírico (en el sentido usual), y no lo es porque la inteligencia es inteligencia sentiente, y en cuanto tal, razón y sentir están indisolublemente unidos. Esta unidad expresa el termino constructivismo sentiente.

La intelección sentiente de la matemática no coincide totalmente con la intelección lógica. En este punto vemos que Zubiri recurre al Teorema de Gödel para asentar "científicamente" la diferencia fundamental entre el razonamiento lógico-formal y el método matemático. Queda justificado que consideremos el Teorema de Gödel como un factor decisivo en la evolución zubiriana, desde su primera filosofía de la matemática — que defiende el método lógico-deductivo de verdades a priori en la matemática—, a su segunda filosofía de la matemática —que defiende el método constructivo-sentiente como vía en la realidad postulada de la matemática—. En sus palabras,

"...Gödel demostró (como repetidamente he recordado) que lo postulado tiene propiedades que no son deducibles de los postulados ni pueden ser lógicamente refutadas por ellos; es que a mi modo de ver son propiedades reales de la realidad matemática, y su aprehensión independiente de los postulados es un punto en que la aprehensión de la realidad no coincide con la intelección lógica. En todo método matemático hay, pues, un doble momento: el momento de verdad necesaria de una afirmación, y el momento de aprehensión de realidad" [142]

El Teorema de Gödel muestra que la matemática no se reduce a una estructura lógica —un sistema de teoremas y demostraciones lógicamente encadenadas—, sino que la realidad matemática tiene una ‘estructura’ propia translógica. [143]

 

2.7.2 Estructura del método constructivo-sentiente de la matemática.

Los momentos del método de toda intelección racional son: 1. sistema de referencia, 2. esbozo de posibilidades, 3. experiencia: com-probación física. Analizamos seguidamente estos tres momentos en el método constructivo-sentiente de la matemática. En ellos se pone de manifiesto el rechazo zubiriano del logicismo-formalismo, y la conjunción del sentir y del construir. El método matemático recoge los dos momentos: el dado e impuesto, la impresión de realidad, y el momento creador: el aporte de la inteligencia.

 

2.7.2.1 Sistema de referencia

El primer momento del método matemático es el sistema de referencia, en el cual nos apoyamos para crear el esbozo de lo que "podría ser" la realidad profunda o la realidad matemática en su fundamento. El sistema de referencia no son estructuras mentales sino que es la realidad campal. El modo que tiene la matemática de referirse a ella es con total independencia. La matemática es una construcción completamente libre respecto del contenido de la realidad campal (ya lo vimos). El modo de referirse la realidad matemática al contenido de la realidad campal es ‘independientemente’.

"La realidad matemática no es una parte o momento de la realidad campal; nada tiene que ver con ésta por razón de su contenido... Aquí, la realidad campal en cuanto realidad es un sistema de referencia según la cual la realidad misma tiene un contenido formalmente independiente de todo su contenido campal. Y esta independencia es justo un modo referencial, el modo de referirse a la realidad campal ‘independientemente". [144]

El sistema de referencia determina no la constatación de lo que algo sería sino una experiencia. El conocimiento no es un sistema de proposiciones lógicamente determinado; a partir de un sistema de referencia, es una marcha hacia la realidad profunda. Sería una ingenuidad sostener que la construcción racional de la realidad matemática, que es realidad profunda, sea el mismo que el contenido de la realidad campal; por ejemplo, el espacio geométrico nada tiene que ver con el espacio pre-geométrico o perceptual, pero éste es sistema de referencia para la construcción libre de aquél.

 

2.7.2.2 Esbozo de un libre sistema de postulados o axiomas.

El modo de tomar la construcción matemática como sistema de referencia el campo de realidad, pero independientemente de su contenido, nos fuerza a tener que dotarla de un contenido libremente construido por postulados o axiomas — recordemos que éstos postulan contenido de realidad profunda y no verdades lógicas—. Este esbozo de un libre sistema de postulados y axiomas es el segundo momento del método. No es algo caprichoso o arbitrario, por el contrario nos viene impuesto por el momento de realidad del sistema de referencia liberado del contenido concreto, esto es de tomar la realidad campal como ámbito.

"Esta independencia [del contenido de la realidad campal] nos fuerza a esbozar un libre sistema de postulados o axiomas (no necesito entrar ahora en esta distinción). Estos postulados son pues la determinación postulada del contenido de la realidad, una realidad numéricamente idéntica a la realidad campal en cuanto realidad"[145]

Este esbozo libre del sistema de postulados o axiomas, nos dice Zubiri, tiene su momento sentiente, y como tal impuesto y dado, en la sugerencia. El momento campal mismo sugiere cuál puede ser la posibilidad de su fundamento. Esta sugerencia es esbozo cuando es sugerencia de actividad de la intelección sentiente. La intelección, por ser sentiente, sugiere; y, por ser sentiente, sólo conoce esbozando.

"Hay, en efecto, realidades postuladas. Estas realidades no han sido postuladas por una simple ocurrencia sino que han sido postuladas por sugerencia de la realidad campal"[146]

Ahora bien, en la construcción libre de la matemática, el matemático inventa posibilidades nuevas que no le son sugeridas por la realidad campal; a esta observación responde Zubiri que esta ruptura con todo lo campal no hubiera sido posible sin las sugerencias de ésta, es decir, entre las sugerencias de la realidad campal está la de no atenerse a ninguna de ellas[147]. La sugerencia nunca alumbra unívocamente un sistema de posibilidades, de ahí que su constitución siempre sea una construcción libre. Sugerencia y construcción libre son, en este punto, los dos momentos del constructivismo sentiente.

"La posibilidad así alumbrada tiene un contenido propio. Este contenido en cuanto posibilidad es siempre algo construido: es construcción. (No hablo de la construcción en el sentido de la teoría de conjuntos). El esbozo de las posibilidades es siempre y sólo un esbozo construido. Ninguna posibilidad intelectiva en cuanto tal está pura y simplemente dada"[148].

Es preciso aclarar que el estatuto de la posibilidad no es de naturaleza lógica sino de naturaleza real. Las posibilidades son posibilidades reales, es decir, que se constituyen en la intelección del mundo real. Y esto es crucial. Lo posible se inscribe dentro de la realidad, posibilitándola. El "podría ser" es modo de ser fundamento de la cosa real campal.

"... es lo que la realidad ‘podría ser’. Es la posibilidad de lo real. El término del ‘hacia’ es por el momento tan sólo un término posible. Como tal está en la realidad como un ‘podría’ de la realidad misma. Es una posibilidad real. El sería’ es realidad en retracción. El ‘podría ser’ es realidad en fundamentación"[149].

En la afirmación o intelección campal, el concepto era el irreal que se realizaba en la realidad postulada, como nota o propiedad suya; en la intelección racional, el "podría ser" es el irreal que se realiza en la realidad postulada como su fundamento. El ‘podría ser’ es modo de posibilitación, no modo de ser nota sino de ser fundamento. Dice Zubiri,

"La diferencia entre el modo irreal y el modo de posibilitación no es una diferencia entre dos posibilidades, sino la diferencia entre la irrealidad realizada como nota (modo irreal) y la irrealidad realizada como fundamento (posibilitación). Lo irreal realizado como fundamento: he aquí lo verdaderamente posible de la razón, el ‘podría ser’."[150]

Frente a todo logicismo y formalismo, es necesario insistir, por una parte, en que la posibilidad es real y, por otra parte, en que no es anterior a lo real sino que pertenece a la realidad, a la respectividad mundanal. El sistema de posibilidades del conocimiento matemático no son meros sistemas de postulados y axiomas consistentes o no-contradictorios. No se trata de posibilidades lógicas sino de posibilidades reales. Por último, la sugerencia de la realidad campal jamás lanza hacia una sola posibilidad real sino hacia múltiples posibilidades reales. La razón las considera cada una "con" (cum) las demás. "Por esto, dice Zubiri, el término del "hacia" más que una mera posibilidad es co-posibilidad". [151]

Así por ejemplo, los distintos sistemas de axiomas y postulados de las Geometrías no son sólo sistemas lógicos, esto es, meras posibilidades lógicas, en cuanto no-contradictorias. No. Cada geometría es una posibilidad real, y esto porque no es construcción lógica (en el pensamiento) sino que es una construcción sentiente (en la realidad). El sistemas de postulados y axiomas se construye libremente desde la sugerencia del sistema de referencia campal, y constituye el "podría ser" del espacio campal en su realidad profunda. Son realizaciones del fundamento de la realidad campal en la realidad profunda, y en cuanto tales, son irreales realizados como fundamentos. Las distintas geometrías son posibilidades no en el pensamiento no-contradictorio, sino en la realidad dada en aprehensión primordial. El principio real que "hace posibles" las posibilidades de los distintos espacios es la espaciosidad. La espaciosidad no es concepto, ni intuición, ni construcción; es una propiedad real de las cosas que posibilita las libres construcciones de los sistemas espaciales. En palabras de Zubiri (tal y como las recoge Ignacio Ellacuría):

"Todas las distintas estructuras espaciales son posibilidades reales, y lo que "hace posible" esas distintas y opuestas posibilidades reales es justo lo que llamo espaciosidad. En cuanto principio de las posibilidades espaciales es un principio estructural. Las distintas posibilidades forman un todo porque todas ellas son "co-posibles". Y este "cum" es lo que constituye el carácter principial de la espaciosidad. La espaciosidad no sólo permite varias posibilidades estructurales, sino que fuerza a que se realice una de ellas. La unidad de co-posibilidades estructurales del espacio es el sistema de la espaciosidad"[152]

Y, en términos similares (tal y como lo recoge Antonio Ferraz), insistimos en esta concepción zubiriana de la Matemática como irreductible a la Lógica:

"La realidad como ámbito tiene un principio estructural, no causal, que es la espaciosidad. Esta no tiene estructura, pero hace posibles las estructuras. Lo "real" de la posibilidad consiste en que "permite" que haya espacios de una o de otra estructura. Las estructuras son co-posibles. Pero la espaciosidad no sólo "permite" varias posibilidades estructurales, sino que "fuerza" a que se realice una de ellas.(...) Como posibilidad el espacio no podría ser arquimediano si no pudiera ser no-arquimediano" [153]

No entramos a analizar aquí la concepción de espaciosidad de Zubiri, lo haremos en el próximo apartado dedicado al realismo matemático. Aquí basta la idea de la espaciosidad como principio de las cosas que hace "reales" las posibilidades espaciales construidas libremente. Noción que nos permite deslindar la posibilidad lógica de la posibilidad real, cuestión clave en todo constructivismo matemático (en su carácter antiformalista y antilogicista), y particularmente en el constructivismo sentiente de Zubiri.

En este desplazamiento de la posibilidad lógica a la posibilidad real como objeto formal del conocimiento matemático, sin duda ha ejercido una gran influencia el Teorema de Gödel, y en concreto el corolario del Teorema de incompletitud (denominado segundo Teorema de Gödel), que dice, en palabras de Zubiri: "jamás podrá demostrarse positivamente la no contradicción de un verdadero sistema de notas o conceptos objetivos"[154]. La consistencia no puede demostrarse en ningún sistema formal que contenga formalizados todos los modos finitos de prueba. Si la consistencia no puede demostrarse, ¿cómo puede seguir siendo el criterio de validez de las construcciones libres de los sistemas de axiomas y postulados de la matemática?

 

2.7.2.3 Experiencia: Com-probación física de realidad

El tercer momento del método consiste en la probación física de realidad, esto es, en la experiencia. Zubiri hace una división, en toda la intelección racional, entre el modo de experienciación ob-vio y el modo de experienciación viable. Y dentro de esta modalidad, distingue cuatro tipos: el experimento, la compenetración, la comprobación y la conformación. El modo de experiencia de las realidades postuladas, esto es, la realidad matemática y la de literatura de ficción, es la com-probación.

En primer lugar, es preciso aclarar qué es experiencia desde inteligencia sentiente, y, sobre todo, tenemos que distinguir ese concepto de otras dos nociones conceptualizadas en inteligencia concipiente: experiencia como percepción y experiencia como mismidad empírica. Ninguno de estos dos modos concipientes pueden ser método de la matemática.

Experiencia no es sentir

El sensualismo es la postura que identifica la experiencia con la percepción o el sentir. Según Zubiri, ya lo vimos, esto es erróneo; en primer lugar, porque el sensualismo ha resbalado sobre el momento de formalidad de lo sentido y sólo se atiene al momento del contenido, pero no a la impresión de realidad. Y es que el sentir es sentir intelectivo y no puro sentir. En segundo lugar, porque sentir y experiencia no se identifican. La razón de ello es que lo sentido en el sentir es algo dado mientras que en la experiencia lo sentido es algo logrado. No es lo dado la esencia de la experiencia sino, por el contrario, su carácter esencial es el logro. Y esto es fundamental.

"Logrado ciertamente sintiendo, pero logrado. Lo sensible no es sino experienciable, pero no es formalmente experienciado. El momento de logro es esencial a la experiencia"[155]

Experiencia no es empeiría

La otra noción de experiencia, desde inteligencia concipiente, es como empeiría, ésta denominación se debe a Aristóteles. La experiencia sería el modo de sentir una cosa "misma", a través de la reiteración de la percepción. Además de que no sólo percibimos las cualidades sino también la impresión de realidad, el momento experiencial es algo distinto. La diferencia entre empeiría y experiencia está en que ésta es la aprehensión de la cosa en profundidad, es aprehensión como real mundanalmente. Usualmente, se ha contrapuesto profundidad a experiencia; el objeto de experiencia sería la superficialidad de las cosas, mientras que de la profundidad de ellas no habría experiencia sino construcción teórica, o conjeturas. Esta contraposición sólo se da en inteligencia concipiente, no en inteligencia sentiente.

Experiencia en inteligencia sentiente: probación física de realidad.

Experiencia, desde inteligencia sentiente, es un logro de profundización. Y esto es probación física de realidad. Probación es lo que la cosa real es en profundidad. Y es probación porque no se trata de realización de un "sería" en la realidad, como en el logos sentiente, sino de realización de un "podría ser" en la realidad. Es probación de realidad de la cosa como momento del mundo. Esto es aplicable a la matemática, y significa que la prueba matemática no es un momento lógico sino que el momento esencial en esta probación es físico. La probación matemática es probación constructivo-sentiente: hay que hacerla en la realidad. Es una ejercitación física qué discierne cuál sea el fundamento mundanal. Y esto, una vez más, es fundamental en la distinción entre Matemática y Lógica.

"En segundo lugar, es una probación física. No se trata de un pensamiento, o de algo semejante. Se trata de una probación "física". Es algo no pensado sino ejercitado. Es "hacer" la probación. Y este ejercicio tiene un carácter esencial. Es algo ejercitado, pero el ejercicio mismo es modo de intelección de lo real en su carácter mundanal. En cuanto ejercitado, es algo físico, y en cuanto intelectivo es la intelección en un abrirse paso ejercitándose. Este abrirse paso es ese momento intelectivo que llamamos discernimiento. Probación física es, pues, ejercitación discerniente" [156]

La probación no es una constatación como se llevaría a cabo en el campo de la realidad sino posibilitación. La probación recae sobre un allende el campo. La esencia de la experiencia es inteligir lo sentido como momento del mundo (en nuestro caso, de la talidad mundanal) a través del fundamento que hemos esbozado en la razón sentiente. Se prueba la realización de algo irreal, el "podría ser" libremente construido en la realidad campal.

Y según este sentido de probación, está claro que, como afirma Zubiri, "sólo una razón sentiente puede hacer probación"[157] puesto que sólo desde ella estamos atenidos a la realidad, sólo desde ella podemos sentir lo real hacia lo profundo sin salirnos de la realidad. La probación se hace en el campo de la realidad, y lo que se prueba es si la realidad mundanal en cuanto fundamento de la realidad campal se inserta o no en la realidad campal. En la probación no salimos de la realidad dada en aprehensión a la realidad "fuera" de la aprehensión, como zona de cosas distinta a nosotros. Es un proceso que se da en la aprehensión de realidad y nos movemos del mundo, al cual nos remitió el campo mismo por la insuficiencia de su contenido, de nuevo otra vez, al campo para verificar en la experiencia la razón de éste.

La probación no es mero ensayo, como si se tratara de un acto mío. Es una probación real. Es la realidad la que prueba o no en su actualización si se inserta el mundo en el campo. Ante la posibilidad de probación de la realidad quedamos en gran parte como expectantes. El resultado de hacer la probación es la experiencia de lo real campal en su fundamento. La realidad campal queda actualizada no desde otras cosas reales del campo sino desde la realidad mundanal, desde su razón. La probación más que mero ensayo es un "intentum", no ensayamos ir a la realidad porque ya estamos en ella; es "estar-tenso-en"

"Porque no se trata tan sólo de la experiencia como actividad mía de ensayo, sino que se trata sobre todo — y en primera línea— de que en esta inserción se actualiza lo real"[158]

El concepto de experiencia expuesto es común para la matemática y para cualquier otra ciencia. En lo que se distinguen, pues, no es en que en un caso el método sea la experiencia y en otro caso fuera el razonamiento deductivo, sino que su diferencia estriba en el modo de experiencia, porque este concepto, como ya hemos dicho, no es único.

Es errónea la reducción de experiencia a experimento, como hace el positivismo, el neopositivismo lógico, Popper, etc. Y en tal caso, al ser evidente que la matemática no es experimento, se le ha negado la experiencia como método propio. Y es que el modo de experiencia de las realidades matemáticas es la com-probación física. Ahora bien, ¿en qué consiste el modo de experiencia matemática: la comprobación?

Anteriormente hemos considerado los dos momentos que Zubiri atribuye al método matemático: momento de verdad y momento de aprehensión de realidad, pues la comprobación matemática consiste precisamente en la unidad intrínseca de esos dos momentos. Por ello es probación-con. Zubiri especifica que lo que se prueba, por tanto, no es si nuestra afirmación es verdadera o no (sería un logicismo), sino la presencia de la realidad "en" la verdad deducida. Si la verdad deducida "A es B" no nos hiciera aprehender la realidad de A "siendo" B, no tendríamos matemática. En palabras de Zubiri,

"A mi modo de ver, la comprobación no consiste en comprobar si mi afirmación se verifica; esto no necesita ser comprobado en matemáticas. Lo comprobado no es la verdad de mi afirmación sino que es la presencia misma de la realidad aprehendida al hilo de la verdad deducida; es la probación de la realidad al hilo del "cum" de la verdad. No se comprueba la verdad sino que se comprueba la realidad en su verdad: aprehendemos la ‘realidad en verdad’"[159]

En este tercer momento del método matemático: la com-probación de la realidad en su verdad, se toca con el dedo la diferencia entre método constructivo-sentiente de la matemática y método lógico-formal. El método matemático, en cuanto probación de la realidad, es un tipo de experiencia. Tenemos experiencia de lo matemático. Aunque no sentimos el contenido de la realidad postulada de la matemática (no es sensible), su probación la llevamos a cabo sentientemente en la realidad, por ser la inteligencia sentiente. (Recordemos la diferencia entre inteligencia sensible e inteligencia sentiente).

"He aquí lo que paradójicamente, pero muy exactamente, debe llamarse experiencia de lo matemático. Lo matemático es término de una probación física de realidad, es término de experiencia"[160]

 

2.7.3. Fin del paradigma científico y filosófico de la matemática "deductiva"

La logificación del método matemático (método deductivo-a priori) ha tenido una repercusión en la logificación de las ciencias, e incluso de la filosofía, en cuanto que se ha pretendido la aplicación del método matemático en ellas. Es el proceso que Zubiri denomina logificación de la intelección en toda la tradición filosófica europea desde los griegos. Vemos este proceso a grandes líneas y según lo traza el propio Zubiri.

El inicio de esta vía se remonta a los griegos, principalmente con Euclides (357?- 275 a.C), Arquímedes(287?-212) y Apolonio (260?-200?); ya el método de la matemática queda estipulado con gran perfección. La aportación griega consiste en presentar las demostraciones matemáticas como una sucesión necesaria de un paso al siguiente, de tal modo que logre un asentimiento universal. El método es el razonamiento de verdades eternas (no temporales ni espaciales). Esta matemática "deductiva" que ha transcurrido a lo largo de los siglos como paradigma de otros conocimientos sólo en nuestra época va a ser objeto de una grave reflexión filosófica.

Zubiri analiza cómo Aristóteles, que es el creador de la lógica, es quien precisa la idea de conocimiento como de-mostración. Ya no es sólo prueba racional sino la articulación interna del "qué" y del "por-qué" de lo que son las cosas. Sólo hay conocimiento cuando tenemos presente la necesidad de que algo sea de un modo y no de otro. La vía que nos lleva a entender las cosas es el logos; y es la lógica la disciplina que trata la articulación interna de los elementos del logos. Se da el paso para la conversión del método en lógica.

"El problema del método se convierte así en ‘lógica’, en una elaboración de la idea misma del Logos; y teniendo en cuenta que la idea es, según llevamos dicho, la forma de las cosas, aquello que formalmente las constituye, se comprenderá que la lógica estudia lo que formalmente constituye el logos; y en este sentido eminentemente real es la lógica algo formal. De esta suerte, la lógica fue el órgano del saber real, aquello que nos permite conquistar nuevas ideas y, con ello, nuevos rasgos de las cosas"[161]

La demostración "es el descubrimiento mediato de ideas", y por eso la demostración no es un simple logos, sino un sil-logismo, añade Zubiri.

"Saber, entender, es entonces raciocinar, discurrir, argumentar. Algo es verdadero en la medida en que el discurso o raciocinio lo manifiesta como necesariamente verdadero; lo demás es incierto o anticientífico"[162]

Esta vía de identificación de saber y de-mostrar se debió, en gran parte, a lo largo de los siglos al éxito de la matemática como paradigma del saber demostrativo y raciocinante, y hasta la propia filosofía ha sido sometida a la "tiranía de este modelo". La crisis de la "matemática deductiva" pondrá en crisis la noción misma de saber o de inteligencia.

Ahondando en la vía demostrativa del saber cabe decir que anterior a la "lógica de los razonamientos" es la "lógica de los principios". Una cosa se sabe en verdad a partir de sus principios. Para Aristóteles "el principio de los principios" es el nous, porque es quien ilumina al objeto y permite ver al hombre. Considera que hay principios generales que el hombre percibe por el mero hecho de existir y que se refieren a las cosas en cuanto tales, así el principio de contradicción. Estos principios son verdades primeras tanto en el plano lógico como psicológico. Los griegos le dieron el nombre de axiomas, esto es, "dignidades". Son verdades en cierto modo absolutas porque no dependen de ninguna otra verdad para que nuestra mente capte que son tales, son, por tanto, en este sentido, connaturales a la propia mente. "Principios son así principios de que algo sea, en verdad, lo que es"[163].

Este método de saber principial culmina en Descartes y en Leibniz. Saber es partir de principios y desde ellos recomponer lo principiado. Ambos son grandes matemáticos y ésta es la ciencia que toman como modelo de saber por proporcionar certezas a través del método deductivo a priori. Es la obra del racionalismo. Prolongando esta vía de la logificación del saber vamos a desembocar al idealismo alemán de Fichte y Hegel. Saber algo es ver cómo a partir del todo se genera lo que algo es. Esta concepción es sistemática y dialéctica.

Esta línea nos presenta la estructura lógica de las cosas, pero no se trata de esto en el saber real; para Zubiri se trata de aprehender la realidad, que es cosa distinta.

"Saber no es sólo entender lo que de veras es la cosa desde sus principios, sino conquistar realmente la posesión esciente de la realidad; no sólo la "verdad de la realidad", sino también la "realidad de la verdad". "En realidad de verdad" es como las cosas tienen que ser entendidas"[164]

Ante los resultados anteriores, Zubiri antepone a la lógica de principios una lógica de la realidad. Esto es una primera formulación del planteamiento "realista" de Zubiri. En la Trilogía de la intelección afirma que la realidad no es lógica sino translógica, respectiva, y por ello inadecuada para ser captada por un instrumento lógico.

A este resultado hemos llegado en la filosofía de la matemática zubiriana: constructivismo sentiente. La matemática no es solamente estructura lógica sino que es también, y sobre todo, aprehensión de realidad matemática. La matemática no consiste en demostraciones a priori, sino en experiencias, en com-probación física de realidad, en el sentido expuesto. Esta conclusión a la que nos ha conducido el análisis del método matemático creemos que es crucial para asentar la concepción realista que tiene Zubiri del saber. El saber es siempre saber de la realidad, actualización de la realidad. Es así porque la inteligencia no es lógica sino que es sentiente.

La propia matemática pone fin al intento racionalista e idealista de aplicar el método deductivo a otras ciencias o tipos de conocimiento. La matemática pone de manifiesto la esencialidad de la aprehensión de realidad junto con la estructura lógica. Por otra parte, es absurdo querer aplicar a todas las realidades el método matemático. La comprobación es el tipo de experiencia adecuado a las realidades postuladas, por tanto es método de las matemáticas y de la literatura de ficción. Esta conclusión de Zubiri resulta realmente provocativa para la concepción racionalista de la matemática.

"Ciertamente hay realidades postuladas que no son matemáticas: constituyen el ámbito de la realidad de ficción. Pero no necesito insistir en ellas porque a todas luces tienen los dos momentos de coherencia interna de lo fingido, y de aprehensión de su realidad en ficción. Son en este sentido término de com-probación, en la forma explicada" [165]

 

2.7.4 Ceguera del Positivismo Lógico para la marcha creadora de la razón.

A lo largo de la primera mitad del s. XX, la filosofía de la matemática y de la ciencia estuvo dominada por los empiristas lógicos o positivistas lógicos, que tomaron el empirismo clásico y el nuevo instrumento de la lógica simbólica como base para sus análisis de la ciencia. Los filósofos de esta tradición se interesaron principalmente por los problemas más lógicos, en particular, por la estructura lógica de las teorías y las relaciones entre los enunciados. Las cuestiones que no son dóciles al análisis formal, como, por ejemplo, la naturaleza del descubrimiento matemático o científico, fueron dejadas de lado como no filosóficas.

Una teoría central de la filosofía del empirismo lógico es la distinción entre el contexto de descubrimiento y el contexto de justificación. La fuerza de esta distinción está en su opción por ocuparse sólo de cuestiones lógicas y que tales cuestiones sólo surgen después de que ha sido formulada una teoría científica. El descubrimiento matemático o científico se relega a la psicología o sociología[166].

El empirismo lógico identifica racional con lógico, del mismo modo que Popper[167]. El objetivo ideal sería alcanzar un algoritmo para probar la verdad o falsedad de una teoría: la lógica inductiva en el primer caso y la lógica deductiva o "modus tollens" en el segundo caso. Según Brown[168], la irracionalidad del enfoque de la racionalidad del empirismo lógico que identifica racionalidad y computabilidad algorítmica consiste en que su puesta en marcha no requiere la presencia del ser humano. Según este autor, la decisión humana no es equivalente en modo alguno a un mero algorítmo. En vez de afirmar que el proceso del descubrimiento científico es irracional, deberíamos considerar al científico que busca activamente la solución de un problema como un caso paradigmático de pensamiento racional.

Este es el estado actual del empirismo lógico. Es lugar común la crítica de los filósofos de la ciencia a esta concepción. A esta crítica se suma Zubiri, pero clarificando enormemente, desde su concepción de racionalidad sentiente, la deficiencia de la concepción de racionalidad del empirismo lógico y de su objeto de estudio. Según Zubiri, el positivismo lógico considera al conocimiento como un sistema de proposiciones lógicamente determinado. Pero esto es meramente una conceptuación de la intelección campal. Reduce la estructura del conocimiento a la del logos.

"el positivismo lógico sólo es una conceptuación —y no completa— de la intelección campal, pero es ciego para la intelección mundanal, cuyo carácter estructural esencial es la direccionalidad"[169]

Es erróneo reducir la intelección mundanal a la intelección campal. El juicio campal no es conocimiento. La estructura formal del conocimiento no se reduce a la estructura formal de los lógoi, sino que envuelve el momento esencial de una referencia direccional. No basta con enunciados de sentido unívoco. El mundo no tiene una estructura lógica sino una respectividad real. No puede identificarse el conocimiento en cuanto descubridor de nuevas direcciones en su marcha en la realidad profunda con su expresión lógica.

"El positivismo lógico se limita a los enunciados lógicos de esta intelección. Pero estos enunciados son tan sólo su expresión lógica, no constituyen la estructura formal del conocimiento que es marcha intelectiva"[170]

Lo esencial del conocimiento matemático y de cualquiera en general, hemos visto que, según Zubiri, es ser creación o descubrimiento, posible en cuanto que la intelección se mueve en la realidad; es libre creación, y esta dimensión es totalmente apartada —como contexto de descubrimiento— del objetivo del filósofo de la ciencia, por parte de los empiristas lógicos. Estos filósofos sólo se ocupan del contexto de justificación, del producto ya acabado de la investigación científica, son completamente ciegos para la dimensión de libre creación de la razón. Se centran sólo en el momento de estructura lógica, y olvidan el momento de aprehensión de realidad.

"El positivismo lógico es ciego para esta dimensión creadora del conocimiento. Porque crear no es enunciar nuevas proposiciones sino descubrir nuevas direcciones de marcha intelectiva. Por esto es por lo que el estatuto cognoscitivo de la intelección racional no es ser constatación "unívoca" sino dirección "fecunda" hacia lo real mundanal."[171]

En definitiva el error del positivismo lógico es la logificación de la intelección y la idea de una inteligencia concipiente. Es la filosofía de la matemática de la escuela "logicista" de la matemática a la que se opone enérgicamente la concepción zubiriana.

"El conocimiento no es un sistema de conceptos, proposiciones y expresiones. Esto sería un absurdo conceptismo, mejor dicho un logicismo en el fondo meramente formal"[172]

Zubiri corrobora que es necesaria la precisión conceptual y el rigor formal, "es menester la reconquista de la exactitud y de la precisión en los conceptos y en las expresiones". Pero esto no significa que esta analítica de la función lógica, dé la estructura del conocimiento. El conocimiento no es constatación unívoca sino dirección precisa.

La razón sentiente no es logos, es inquiriencia, su modo de inteligir es marchando en búsqueda del contenido profundo, en la realidad misma; es marcha intelectiva; tiene como momento estructural la fecundidad y no como mero resultado

 

 

3. ULTIMIDAD SENTIENTE DE OTROS CONSTRUCTIVISMOS DE LA MATEMATICA

 

Una vez analizado ¿Qué es el constructivismo sentiente de la matemática?, nos proponemos en el presente capítulo poner de manifiesto la ultimidad de la filosofía sentiente de la matemática y su corolario: la filosofía concipiente de la matemática se fundamenta en la filosofía sentiente de la matemática. Las distintas filosofías de la matemática, desde la inteligencia sentiente, no son falsas, ni incompatibles, pero sí unilaterales e insuficientes en la línea de su fundamentación.

Examinamos a continuación, a la luz del constructivismo sentiente, la noción de la construcción matemática según la definen:

1. El constructivismo sensible de Kant.

2. El axiomatismo formalista de Gödel y Cohen.

3. El intuicionismo de Brouwer y Heyting.

 

3.1. Desviación de la construcción sensible de la razón pura en Kant.

La filosofía constructivista de la matemática de Kant tiene una gran actualidad. La limitación de los sistemas formales y lógicos y la irreductibilidad de la Matemática a la Lógica — puestas de relieve por los teoremas de incompletitud de Gödel, indecidibilidad de Church e indefinibilidad de Tarski —, conducen, en numerosos autores (Hintikka, Kitcher, Friedmann, Parsons, etc.), a una consideración nueva de los planteamientos constructivistas kantianos de la matemática. Este interés despertado por Kant ha llevado a los estudiosos a considerar su concepción de la matemática como la primera filosofía de la matemática —frente a la visión ortodoxa que la atribuía a Frege—. Si bien Kant tiene el indiscutible mérito de ser fuente del actual constructivismo de la matemática, esta "vuelta a Kant" no puede ser incondicional, puesto que son graves los problemas que se plantean desde su concepción: ahistoricismo, imposibilidad de explicar la pluralidad de geometrías, finitismo, etc.

Este es el reto actual: pensar sobre la matemática en diálogo con Kant, mas tratando de superar su planteamiento. Y esta tarea la acomete Zubiri de modo sumamente original y fecundo. Parte del constructivismo igual que Kant, pero no sensible sino sentiente. Y esta diferencia es radical. Veremos, pues, a continuación:

1. Las convergencias del constructivismo kantiano y zubiriano.

2. Las divergencias del carácter sensible y el carácter sentiente de los constructivismos de Kant y de Zubiri, respectivamente.

3. Y, por último, mostraremos que el constructivismo sentiente tiene las ventajas del constructivismo sensible, en cuanto constructivismo, y, a la vez, supera las dificultades que éste, en cuanto sensible, tiene planteadas.

Como resultado de nuestro análisis, la filosofía de la matemática de Zubiri se nos presentará como una auténtica alternativa a la filosofía de la matemática kantiana y vendrá a ocupar el puesto que ésta tiene como interlocutor ineludible en cualquier cuestión actual de epistemología y ontología matemática.

 

3.1.1. Kant y Zubiri: coincidencias de la matemática constructiva.

3.1.1.1 La matemática: piedra angular de la unidad de razón y experiencia.

La situación intelectual de Kant y de Zubiri viene definida, en gran parte, por un antagonismo entre racionalismo y empirismo, el cual plantea el problema gnoseológico de qué papel desempeñan en el conocimiento tanto la intuición o sensibilidad como la lógica o pensamiento. Esta cuestión es crucial en la Matemática, de ahí que ésta ocupe un puesto privilegiado en las obras capitales de Kant y de Zubiri. En efecto, la Crítica de la Razón Pura y la Trilogía sobre la intelección son tratados sobre la intelección (Kant identifica intelección con conocimiento) e implícitamente contienen una filosofía de la matemática. Mostrar que esto es así en Zubiri es uno de los objetivos de nuestra tesis. Y en el caso de Kant, ha sido puesto de relieve por numerosos autores, por ejemplo Brunschvicg, quien en Las etapas de la filosofía matemática, nos dice:

"la filosofía matemática ha llegado a ser la piedra angular de la Crítica de la razón pura" [173]

El texto al que alude el autor para asentar esta tesis nos parece que es clave. Kant — en el contexto del problema general de la razón pura: ¿cómo son posibles los juicios sintéticos a priori?— hace la observación de que la matemática torna problemática la validez de la teoría empírica de Hume. Llevada a sus últimas consecuencias afectaría a la certeza de la matemática, porque, según el autor, esta disciplina está formada por juicios del mismo tipo que los juicios de las otras ciencias. Dice Kant:

"David Hume, el filósofo que más penetró en este problema, pero sin ver, ni de lejos, su generalidad y su concreción de forma suficiente, sino quedándose simplemente en la proposición sintética que liga el efecto a su causa (principium causalitatis), creyó mostrar que semejante proposición era totalmente imposible a priori. (...) Si Hume hubiese tenido presente nuestro problema en su universalidad, jamás se le habría ocurrido semejante afirmación, que elimina toda filosofía pura. En efecto, hubiera visto que según su propio razonamiento, tampoco sería posible la matemática pura, ya que ésta contiene ciertamente proposiciones sintéticas a priori. Su sano entendimiento le hubiera prevenido de formular tal aserto"[174]

La Matemática en ambos casos, en Kant y Zubiri, es fuente de sugerencia de una nueva noción de conocimiento, que unifica deducción formal y experiencia, aplicable a todas las ciencias. Tanto uno como otro, pretenden dar una solución gnoseológica que supere el dogmatismo racionalista y el escepticismo empirista. Ni el logicismo-formal, ni el intuicionismo, son adecuados para la intelección matemática, de ahí la aportación constructiva de nuestros filósofos, que viene a "poner fin al antagonismo del concepto y de la intuición". El interés filosófico de la matemática es, pues, de primera magnitud. En palabras de Brunschvicg:

"El prestar atención a la realidad específica del saber matemático da el medio de sustraerse a la estrechez de los prejuicios dogmáticos; pone fin al antagonismo del concepto y de la intuición, que amenazaba agotar a la filosofía en una polémica abstracta y sin salida; y conduce a una solución objetiva y positiva del problema de la verdad"[175]

 

3.1.1.2 El conocimiento matemático: irreductible al razonamiento lógico-formal.

Desde la línea constructivista de la matemática, tanto Kant como Zubiri rechazan el mero logicismo y formalismo de la matemática. La Matemática no se reduce a la Lógica, como pretenden Leibniz (en el contexto de Kant), Frege y Russell (en el contexto de Zubiri). No basta el pensamiento lógico-formal, como tampoco es suficiente la mera intuición, para proporcionarnos el conocimiento matemático. Se precisa las dos componentes. La matemática no es un sistema de conceptos lógicos, sino que para ser conocimiento requiere la unidad de intuición y concepto (en el próximo punto precisaremos la índole de esta unidad en Kant y en Zubiri). Exponemos seguidamente distintos aspectos de esta irreductibilidad de la Matemática a la Lógica.

A diferencia de Leibniz y los logicistas, Kant y Zubiri piensan que los principios lógicos: de identidad y de no-contradicción no tienen la función de fundamentar los juicios constructivos matemáticos, tan sólo tienen una función constrictiva y orientadora. La construcción matemática ha de respetarlos, pero no son fuente de verdad matemática porque no proporcionan un contenido nuevo. Esto lo hemos visto sobradamente en Zubiri. Y en Kant son significativas sus palabras:

"Aunque algunos de los principios supuestos por los geómetras son analíticos y se basan en el principio de contradicción, sólo sirven, al igual que las proposiciones idénticas, como eslabones del método, no como principios. Por ejemplo: a=a, el todo es igual a sí mismo, o bien (a+b) es mayor que a, el todo es mayor que una de sus partes. Sin embargo, estos mismos principios sólo se admiten en matemáticas, a pesar de ser inmediatamente válidos por sus meros conceptos, en cuanto que son susceptibles de representación intuitiva"[176]

Y más adelante, nos dice que si un juicio matemático fuera contradictorio, ciertamente no podría ser verdadero o ser objeto matemático, mas del hecho de que no sea contradictorio no podemos deducir que sea verdadero, pudiera ser que fuera incontradictorio y, no obstante, falso. La consistencia formal no es el criterio de existencia del objeto matemático. Dicho de otra manera, la posibilidad real del objeto matemático no se reduce a la posibilidad lógica de los conceptos. Esta distinción es clave en nuestros dos autores. Nos dice Kant:

"La ausencia de contradicción interna constituye la condición universal —aunque sea únicamente negativa— de todos nuestros juicios... Pero aun en el caso de hallarse exento de contradicción, el juicio puede ligar conceptos de modo distinto al requerido por el objeto... Así, pues, un juicio puede ser falso, o carecer de fundamento, a pesar de estar libre de toda contradicción interna"[177]

Los conceptos matemáticos se obtienen por construcción y no por derivación o deducción lógica. La intelección matemática de los conceptos es constructiva. Recordemos que para Zubiri construir un concepto consiste en proyectar el contenido libremente creado en la impresión de realidad dada primordialmente. Para Kant se trata de proyectarlo "a priori" en la intuición pura, de modo que se materialice en un contenido sensible. Dice Kant:

"En cambio, determinar una intuición a priori en el espacio (figura); dividir el tiempo (duración); conocer simplemente el elemento universal de la síntesis de una misma cosa en el espacio y en el tiempo, así como la magnitud a que ello da lugar en una intuición en general (número); todo esto es tarea de la razón mediante la construcción de conceptos, tarea que calificamos de matemática " [178]

Un ejemplo de construcción de conceptos matemáticos,

"Si se tratara del concepto matemático de triángulo, lo construiría, es decir, lo daría a priori en la intuición, con lo cual lograría un conocimiento sintético y, además, racional"[179]

Y del mismo modo que los conceptos no son elementos lógicos, tampoco los juicios y los razonamientos son una operación mental; no se obtienen por mero análisis de los conceptos o por encadenamiento de juicios, respectivamente, sino por construcción. Lógica y método matemático no se identifican. La demostración lógica no es suficiente como método matemático, es mero organon del conocimiento. El método no es vía en el pensamiento sino en la intuición pura (Kant) o en la realidad dada por la aprehensión primordial (Zubiri). Ya vimos que es así en Zubiri. En cuanto a Kant, nos dice que los juicios y razonamientos matemáticos no son deducciones o derivaciones formales sino procesos de construcción sintética. La construcción, a diferencia de la deducción, aporta algo nuevo en cada paso. Según este filósofo, todos los juicios matemáticos son construcciones sintéticas. En aritmética pone el ejemplo del juicio sintético a priori: "7+5=12"; no es analítico, nos dice, porque el predicado "12" no esta contenido en el sujeto "7+5"; por más vueltas que demos a los conceptos no hallaremos la suma, se requiere la operación de síntesis de los conceptos con la intuición, esto es, la operación de contar. Dice Kant:

"El concepto de suma de 7 y 5 no contiene otra cosa que la unión de ambos números en uno solo, con lo cual no se piensa en absoluto cuál sea ese número único que sintetiza los dos. El concepto de 12 no está todavía pensado en modo alguno al pensar yo simplemente dicha unión de 7 y 5. Puedo analizar mi concepto de esa posible suma el tiempo que quiera, pero no encontraré en tal concepto el 12. Hay que ir más allá de esos conceptos y acudir a la intuición correspondiente a uno de los dos, los cinco dedos de nuestra mano, por ejemplo,... e ir añadiendo sucesivamente al concepto de siete las unidades del cinco dado en la intuición" [180]

En geometría, pone como ejemplo de juicio sintético: "la línea recta es la más corta entre dos puntos". Y aclara que es sintético porque en la cualidad "recta" no entra el concepto cuantitativo "corta", lo cualitativo y lo cuantitativo son dos órdenes distintos. Por tanto, hay que recurrir a la intuición para elaborar la síntesis.[181]

A pesar de estas coincidencias de Kant y Zubiri respecto a sus concepciones constructivistas frente al logicismo y formalismo, ya quedan esbozadas en lo expuesto profundas diferencias, que nos dejan las dudas siguientes: la construcción ¿es sensible o sentiente?, la unidad de intuición y concepto o entre varios conceptos (Sujeto y Predicado) ¿es sintética o de despliegue?, el sentir lo matemático ¿es en la línea de la formalidad o en la línea del contenido?, la base sobre la que se proyecta o aplica el concepto para realizar su construcción ¿es una estructura a priori de la sensibilidad del sujeto transcendental o es una estructura transcendental de la realidad dada en aprehensión primordial? Son cuestiones, a nuestro modo de ver, de suma gravedad porque originan enfoques radicalmente diferentes. Lo analizamos a continuación.

 

3.1.2 Kant y Zubiri: divergencias del constructivismo sensible y el constructivismo sentiente.

3.1.2.1 Intuición y concepto: ¿unidad sensible-sintética o unidad sentiente-de despliegue ?

El propio Zubiri establece diferencias radicales entre su concepción y la kantiana. La raíz de todas ellas está en la distinción entre sensible y sentiente, que más allá de ser caracteres de dos tipos de constructivismos matemáticos, son, en realidad, caracteres de dos concepciones de inteligencia, a saber, inteligencia sensible e inteligencia sentiente. En la "noología" de Zubiri hemos analizado la distinción que hace el autor entre inteligencia sensible o concipiente (legada por la tradición filosófica europea) y la inteligencia sentiente (aportación original suya), ahora nos preguntamos ¿qué papel juega el constructivismo kantiano en esta diferenciación? Para responder tengamos en cuenta lo siguiente:

1. Zubiri cuando afirma que se toca con el dedo toda la diferencia entre inteligencia sensible e inteligencia sentiente, se refiere, como ya pusimos de relieve, al modo de sentir lo matemático.

2. Zubiri expone su concepción de la inteligencia y de la relación entre intuición y concepto en confrontación directa con las ideas de la Crítica de la Razón pura —que tiene como piedra angular la Matemática—.

A la vista de estas dos observaciones, cabe inferir, sin temor a equivocarnos, que el campo de la interpretación matemática y el diálogo con el constructivismo matemático kantiano son dos coordenadas que han trazado un horizonte intelectual preciso, desde el cual Zubiri se esfuerza por dilucidar la clave de la filosofía matemática (y de la filosofía en general), a saber, qué tipo de unidad existe entre sentir e inteligir y, consecuentemente, entre intuición y concepto (exigencia impuesta también por el Teorema de Gödel).

La dificultad de la filosofía matemática de Kant para dar cuenta, por ejemplo, de las geometrías no euclídeas y de la matemática transfinita de Cantor, lleva a Zubiri a replantearse el modo de construcción matemática y el modo supuesto de intelección. En primer lugar, se preguntará Zubiri, ¿cuál es la concepción de la inteligencia que está implícita en la filosofía kantiana de la matemática? Según Kant, el sujeto cognoscente tiene dos facultades: la sensibilidad (receptiva) y el entendimiento (espontánea). La primera aporta intuiciones (que son sólo sensibles) y la segunda produce conceptos. El conocimiento requiere la síntesis de las dos facultades. Zubiri sintetiza la filosofía de Kant en los siguientes términos:

"Siguiendo la línea del intuicionismo y del racionalismo, podría pensarse que intuición y razón son dos "fuentes del conocimiento". En su virtud su unidad consistiría en constituir un solo conocimiento. Es la filosofía de Kant"[182]

Para Kant, sólo la intuición o sólo el concepto no proporcionan conocimiento, es necesario la unidad de intuición y concepto. Es célebre su afirmación de que la intuición por sí misma es "ciega" sin el concepto, y el concepto de por sí es "vacío" sin la intuición. Así pues, la representación del objeto sólo es resultado de la síntesis del concepto y la intuición. El objeto del conocimiento es término de esta síntesis. La intuición nos da multitudes de cualidades sensibles del objeto configuradas espacio-temporalmente. Pero no son "el" objeto mismo. Esta unidad la proporciona el concepto. Kant trata de superar la dualidad intuición y concepto, pero acepta estos términos tal y como le son legados por la tradición racionalista y empirista. Dice:

"...sin sensibilidad ningún objeto nos sería dado y, sin entendimiento, ninguno sería pensado. Los pensamientos sin contenido son vacíos; las intuiciones sin conceptos son ciegas... Ni el entendimiento puede intuir nada, ni los sentidos pueden pensar nada. El conocimiento únicamente puede surgir de la unión de ambos" [183]

Zubiri condensa en una frase la postura de Kant para criticarla a continuación:

"la unidad de intuición y concepto es así ‘unidad sintética’ en el objeto de conocimiento.

¿Es esto así? No lo pienso" [184]

Desde el punto de vista zubiriano, la postura kantiana adolece de una radical insuficiencia, debida al hecho de no comenzar su crítica por el término de "impresión sensible". Tarea que sí acomete Zubiri, y lo hace con tal minuciosidad, según hemos visto, que se asemeja al mejor cirujano sajando los tejidos más delicados. Y, claro está, los resultados "terapéuticos" de esta "operación" (como diría el segundo Wittgenstein) son inmediatos: se disuelven una serie de problemas epistemológicos, por ejemplo, cómo es posible la síntesis entre sentir e inteligir, entre intuición y concepto, etc. No existe, nos dice Zubiri, tal dualidad entre sentidos e inteligir, entre concepto e intuición. La impresión no sólo es sensible (de las cualidades), sino que es también impresión inteligible o transcendental (de la realidad). El análisis zubiriano de la impresión "pone fin", pues, al "cuadro esquizofrénico" (disociación entre sentir e inteligir, entre intuición y concepto... ) que padece la filosofía clásica, y de modo singular la filosofía de la Matemática. Dice Zubiri:

"Como toda la filosofía precedente, Kant recibe sin crítica la idea de impresión sensible como mera afección subjetiva; pero le falta el momento de impresión de realidad. La Crítica no tendría que haber sido ante todo una crítica del conocimiento, sino una crítica de la impresión misma" [185]

El resultado de esta crítica de la impresión, nos dice Zubiri, es constatar que

"Toda intuición humana es intelectiva, y toda intelección humana es sentiente. La unidad de intuición y concepto no es unidad de objeto y cualidad sino unidad de formalidad: unidad de realidad"[186]

Por ser la inteligencia sentiente y el sentir intelectivo,

"...ni la intuición es primariamente ciega, ni el concepto es primariamente vacío"[187]

Insistentemente, Zubiri niega que haya dos fuentes de conocimiento: sentir e inteligir y, enérgicamente, sostiene que la inteligencia es sentiente. La diferencia entre intuición y concepto, no está en la vía de las facultades, sino que está en la vía de los modos de actualización de la realidad. La intuición es el modo de actualización de la aprehensión primordial de realidad, y el concepto es el modo de actualización diferencial o medial de realidad. Entre concepto e intuición hay unidad de intelección y unidad de formalidad de realidad. El hecho de que Kant no haya visto esta unidad esencial se debe a que se ha fijado sólo en la línea del contenido y en ella trata de realizar la síntesis de concepto e intuición. Pero, repetimos, en la intelección no se trata, de modo primario y radical, de la unidad en la línea del contenido sino de la unidad en la línea de la formalidad de realidad. Esto es esencial. Sólo desde este punto de vista puede decir Zubiri que la unidad entre intuición y concepto no es de síntesis (como supone Kant) sino de despliegue. Con sus palabras:

"[la unidad de intuición y concepto] no es ‘unidad de síntesis’ sino ‘unidad de despliegue" [188]

Al ser el concepto mero despliegue de lo intuido, hay que corregir a Kant en dos sentidos: 1. la intuición no es ciega, sino que es ella la que hace vidente al concepto. 2. el concepto no es vacío porque es la realidad aprehendida intuitivamente en forma de "sería".

"Contra lo que Kant pretende, no es el concepto lo que hace vidente a la intuición, sino la intuición la que hace vidente al concepto. Y a su vez, el concepto no es una mera referencia al objeto, sino a la realidad aprehendida en intuición, retraída y desplegada en forma de ‘sería’ "[189]

Así pues, desde el punto de vista de la formalidad de realidad o de los modos de intelección de lo real, no hay contraposición entre intuición y concepto, hay unidad de despliegue. La intuición, de modo radical, se correspondería con lo que Zubiri denomina aprehensión primordial de realidad, y el concepto con la aprehensión diferencial o mediada. La impresión de realidad se nos da en la aprehensión primordial, de ahí que sea la forma suprema de inteligir, ahora bien resulta insuficiente diferencialmente, por esto se despliega en aprehensión diferencial,

"la aprehensión diferencial no sólo está fundada en la aprehensión primordial sino que está formalmente exigida por ésta". [190]

Por esto no hay meramente intuición "y " intelección racional, como si la "y" significara "a la vez", o "unidad sintética", sino que esa diferencia se inscribe en la unidad de actualización o de intelección. En frase lapidaria, al modo como formulara Kant la suya, pero en contraposición a ésta, Zubiri determina la unidad de despliegue, en la línea de la formalidad, entre intuición y concepto, del modo siguiente:

"El concepto es intuición exacta: la intuición es exigencia de concepto, esto es, de despliegue" [191]

Esta aportación zubiriana arroja nueva luz sobre el problema kantiano de la naturaleza de los juicios matemáticos. Kant señala que todos los juicios matemáticos son sintéticos. ¿Es esto así? Lo examinaremos a continuación.

3.1.2.2 "7+5= 12": ¿es un juicio sintético?

Recordemos que "el problema del juicio" constituyó la materia sobre la que versó la tesis doctoral de Zubiri, es una cuestión capital porque refleja la noción de inteligencia, el tipo de relación entre intuición y concepto, y la concepción de verdad, de los que se parte. Veremos que la contraposición entre el constructivismo sentiente de Zubiri y el constructivismo sensible de Kant se hace explícita en la teoría del juicio matemático. Por ello le dedicamos una especial atención.

Hemos visto que la tesis fundamental de la filosofía de la matemática kantiana es que los juicios de la matemática son todos juicios sintéticos a priori. En aritmética pone el ejemplo que ahora nos ocupa: "7 más 5 igual a 12". El predicado no está contenido en el sujeto porque al pensar la unión de 7 más 5 no pensamos el concepto de 12; por tanto, no es analítico sino que es sintético. La síntesis de los dos conceptos la llevamos a cabo en la intuición: contando. Así pues, en el juicio matemático, sintetizamos dos conceptos con base en la intuición. Dice Kant:

"Se podría pensar, de entrada, que la proposición 7+5 = 12 es una simple proposición analítica, que se sigue, de acuerdo con el principio de contradicción, del concepto de suma de siete y cinco"[192]

Esto es lo que han pensado tanto los racionalistas como el propio Hume. Un juicio matemático sería idéntico a un juicio lógico. Sin embargo, continúa diciendo Kant,

"Pero, si se observa más de cerca, se advierte que el concepto de suma de siete y cinco no contiene otra cosa que la unión de ambos números en uno solo, con lo cual no se piensa en absoluto cuál sea ese número que sintetiza los dos. El concepto de doce no está todavía pensado en modo alguno al pensar yo simplemente dicha unión de siete y cinco. Puedo analizar mi concepto de esa posible suma el tiempo que quiera, pero no encontraré en tal concepto el doce".[193]

Kant —después de oponerse a la opinión habitual de que la construcción de un juicio matemático es una operación analítica— ofrece su concepción de la matemática como construcción sensible.

"Hay que ir más allá de esos conceptos y acudir a la intuición correspondiente a uno de los dos, los cinco dedos de una mano, por ejemplo, o bien (como hace Segner en su Aritmética) cinco puntos, e ir añadiendo sucesivamente al concepto de siete las unidades del cinco dado en la intuición. En efecto, tomo primero el número 7 y, acudiendo a la intuición de los dedos de la mano para el concepto de 5, añado al número 7, una a una (según la imagen de la mano), las unidades que previamente he reunido para formar el número 5, y de esta forma veo surgir el número 12. Que 5 tenía que ser añadido a 7 lo hemos pensado en el concepto de suma = 7+5, pero no que tal suma fuera igual a 12". [194]

Y, por último, Kant extrae la conclusión de que los juicios aritméticos (y lo mismo dirá de los juicios geométricos) son siempre sintéticos.

"Por consiguiente, la proposición aritmética es siempre sintética, cosa de la que nos percatamos con mayor claridad cuando tomamos números algo mayores, ya que entonces se pone claramente de manifiesto que, por muchas vueltas que demos a nuestros conceptos, jamás podríamos encontrar la suma mediante un simple análisis de los mismos, sin acudir a la intuición".[195]

¿Es esto así? Según Zubiri, es un planteamiento inadecuado en su mismo punto de partida: inteligencia sensible o concipiente. Presentamos a continuación su crítica a la concepción de juicio sintético en sus dos etapas de filosofía de la matemática: 1. etapa objetivista, y 2. etapa realista.

1. En su etapa objetivista, concretamente en su tesis doctoral, Teoría Fenomenológica del Juicio, el joven Zubiri, critica:

a) la concepción kantiana de juicio

Para Kant juzgar es "subsumir una intuición en un concepto". Se incluye el sujeto en la extensión del predicado. El predicado determina al sujeto. El resultado es una construcción. La radicalización de esta postura la lleva a cabo el neokantismo (Cohen, Natorp). Zubiri considera que el juicio es precisamente lo contrario de esta doctrina: el juicio no puede consistir en que el predicado determine al sujeto, sino, viceversa, que el sujeto se exprese en el predicado.

"Para nosotros todo juicio tiene por supuesto fundamental un objeto, con todas sus determinaciones reales, anterior e independiente, en su contenido, de toda conciencia; el juicio consistiría precisamente en la intención mental de conformarse con ese objeto originariamente dado y no producido. En cambio en el neokantismo ocurre todo lo contrario. El objeto es objeto por su conformidad con las leyes del pensamiento; el juicio es el proceso creador del objeto".[196]

Es un error, para el autor, confundir el sujeto gramatical con el sujeto lógico. En el sujeto lógico, que es el objeto, siempre estará contenido la propiedad enunciada en el predicado; otra cuestión es si en el sujeto gramatical está contenido todo el objeto. Por otra parte, sujeto y predicado no son de la misma naturaleza; el ser del sujeto es real mientras que el ser del predicado es intencional. Por ello, el juicio consiste en ver en el objeto (sujeto lógico) la realidad de lo que en el predicado es intencional. El predicado, pues, no añade nada nuevo al sujeto; si queremos hablar de añadir, es el sujeto quien añade objetividad al predicado.

"La propiedad designada en el predicado no es más que intencional. El juicio tiene por misión afirmar la objetividad de ese predicado en el sujeto" [197]

Según esta concepción del juicio del joven Zubiri, se deduce que todo predicado (intencional) ya está contenido en el sujeto (real), y por tanto, todo juicio es analítico, como vemos a continuación.

b) la clásica división de los juicios en analíticos y sintéticos

El joven Zubiri se pregunta si es correcta esta división de los juicios en analíticos y sintéticos, sobre la que Kant apoya toda su filosofía. Está en desacuerdo con la afirmación kantiana de que sólo lo sensible nos sea dado y que la relación sea producida por el sujeto. Por el contrario, mantiene, al respecto, tres tesis en Teoría Fenomenológica del Juicio :

1. nos es dado tanto lo sensible como lo inteligible;

2. todo juicio, en sentido lógico, es analítico, y

3. toda relación es dada y no producida.

Por tanto, concluye que, desde el punto de vista lógico, es errónea la división de los juicios en analíticos y sintéticos, todos ellos son dados y, en cuanto tales, analíticos. La única diferencia será psicológica y normativa, pero no lógica. El joven Zubiri dice[198]:

"El objeto nos es dado por los sentidos. Sea; pero una vez dado, la conciencia aprehende diversos aspectos o contenidos de él. Los sentidos aprehenden el aspecto sensible; el entendimiento, el aspecto inteligible (...) En rigor, si el juicio quiere ser verdadero, su objeto debe contener el predicado, condición sin la cual el juicio no podría ser válido, y sería arbitrario. En este sentido, todo juicio es analítico, so pena de ser falso"[199]

Kant para distinguir los juicios matemáticos de los juicios lógicos, considera que los primeros no son analíticos sino sintéticos; pues bien, el joven Zubiri le critica el hecho de que no distinga entre el juicio, que siempre es analítico, y la relación de lo juzgado que puede ser analítica o sintética, pero en cualquier caso siempre es dada y no producida. De ahí que Zubiri afirme que los juicios matemáticos son analíticos, como los de cualquier otro tipo; si bien inicialmente hay una creación de los objetos matemáticos, a partir de ellos, se obtienen todos los juicios matemáticos de modo analítico.

"el concepto de síntesis a priori tiene especial aplicación al dominio de las hipótesis y de los postulados. La síntesis, por lo mismo que es a priori crea su propio objeto: tal es el caso de las matemáticas, que crean arbitrariamente su objeto a base de postulados. Pero una vez creado el objeto, la conciencia obtiene todos los juicios analíticamente". [200]

2. En su etapa realista, concretamente en Inteligencia y Logos, el Zubiri maduro plantea en otros términos el problema.

En primer lugar, hay que señalar que Zubiri rechaza tres presupuestos de Kant:

a) la función primaria de la inteligencia no es juzgar, sino que es aprehender impresivamente lo real,

b) la matemática no es un conjunto de juicios, sino de actualizaciones de lo real,

c) los conocimientos matemáticos no son tanto juicios predicativos con la estructura lógica: S es P, cuanto descripciones de carácter funcional[201].

En segundo lugar, hay que precisar que las nociones de "analítico" y "sintético" no son adecuadas para definir las intelecciones campales de la matemática. En la etapa anterior hay un barrunto de lo que nos dirá posteriormente. Ahora, desde inteligencia sentiente, nuestro filósofo defiende que la intelección es noérgica y no noética, esto es, en ella se nos da la realidad con una fuerza de imposición. La realidad misma está presente en la aprehensión primordial. El logos y la razón están determinados por la exigencia de esta realidad aprehendida. Por eso, en el ejemplo de juicio matemático que nos ocupa "7 más 5 igual a 12", nos dice Zubiri que es la aprehensión primordial de "7 más 5" la que determina o exige desde sí misma la realización en ella de la simple aprehensión "12", y no cualquier otra. El concepto clave para entender lo específico del juicio es la evidencia.

"Ver que siete más cinco son doce no es evidencia sino videncia, esto es mera constatación. Sólo el ver que en siete más cinco se realiza no el número 14 sino el 12, porque la actualización de 12 está exigida por la actualización de la suma de 7 más 5, sólo esta visión exigencial, digo, hace que la afirmación sea evidente".[202]

En el primer caso del texto de Zubiri tendríamos una aprehensión primordial de realidad (videncia o mera actualización de lo real en y por sí mismo); en el segundo caso una intelección diferencial o mediada (evidencia o determinación de lo real entre otras cosas del campo). Fijándonos en el segundo caso, en la afirmación se trata de una nueva actualización de la misma realidad dada en la aprehensión primordial de realidad "7+5", pero en su momento campal 12. Entre la primera noción y la segunda hay una fuerza exigencial de lo real o una exigencia evidente de la realización de la simple aprehensión 12 en la cosa, "7+5", ya aprehendida primordialmente. Vemos que "7+5", actualizado en aprehensión primordial, es en realidad 12 . De las simples aprehensiones 12, 14, etc., constatamos que "7+5" realiza la simple aprehensión 12 y no la simple aprehensión 14. Pero entonces no se trata, en la afirmación, de la determinación añadida de 12 sobre 7+5, sino que, por el contrario, es una visión mediada desde "7+5"; es una visión exigida por ésta. Por tanto, según nuestro filósofo, la actualización de la realidad "7+5" es visión exigencial de realización de la simple aprehensión 12.

Recordemos que juzgar, según Zubiri, es afirmar la realización, no la conceptualización, de una simple aprehensión en una cosa real, exigida por ésta misma. La realidad "exige" su determinación diferencial. La exigencia de la intelección de 7+5 constituye la intelección de la realización del 12. Ahora bien, 12 no está contenido en la actualización de 7+5, (en tal caso sería un juicio analítico), tampoco es un mero añadido (en tal caso sería un juicio sintético) que determine lo que es 7+5. Por esto, decíamos que los términos "analítico" y "sintético" no son adecuados para denominar la especificidad de los juicios matemáticos (y del tipo que sean). El juicio no es una aprehensión inmediata y en cuanto tal dada, sino que es una aprehensión mediada, y por consiguiente lograda. La realización de "12" es exigida por la actualización de "5+7". Ex significa hacer salir "desde dentro". Es clara la oposición de ex-igencia y de síntesis. Síntesis significa "añadir enteramente desde fuera". Es la diferencia entre la unidad sintética y la unidad de despliegue, entre intuición y concepto, en el juicio. Si se considera a la cosa real aprehendida "7+5" como un sistema de notas dadas, está claro que ninguna de éstas es "12". Pero es que para Zubiri, además de notas, la cosa real tiene un sistema de exigencias dadas del mismo modo como nos son dadas las notas reales. Por ello 12 está dado en "7+5", no como nota real, sino como exigencia, de ahí que sea término de evidencia.

"La cosa real inteligida no es sólo un sistema de notas sino también un sistema de exigencias. Y el término formal de la evidencia es la discriminación de exigencias, no distinción de notas. Cada cosa y cada aspecto de ella tiene sus propias exigencias articuladas de un modo sumamente preciso" [203].

La realización, nos dice Zubiri:

"Por un lado es un ‘aporte’, por así decirlo, de muchas simples aprehensiones, pero por otro es una "selección" exigencial tanto de las simples aprehensiones que quedan excluidas como de las que quedan incluidas en la intelección. La realización de estas últimas está exigencialmente determinada por la cosa real: es una determinación exigencial intelectiva, que acontece en selección"[204]

En la actualidad diferencial de la realidad, se nos da la impresión de realidad pero no su contenido campal; éste es logrado, mas no como un añadido. El sujeto cognoscente, "arrastrado" por la imposición de la fuerza exigencial de la realidad actualizada, aporta sus simples aprehensiones que la propia realidad selecciona. Más adelante, en el problema de la verdad matemática explicaremos detenidamente la cuestión de la evidencia de los juicios matemático y la de su exactitud. Mencionamos, simplemente de paso, que 7+5=12 es un juicio exacto porque 12 está exigido por 7+5. Por otra parte, el carácter de evidencia no le viene a los juicios matemáticos de que sean síntesis "a priori", como piensa Kant. Los juicios matemáticos no son "a priori", sino que, como ya hemos dicho, son la realización de una simple aprehensión en la impresión de realidad postulada. Todos los juicios encierran evidencia, no sólo los matemáticos, y de este modo todos los juicios están en la línea de la exactitud. Lo explicaremos en el capítulo de la verdad matemática.

 

3.1.3 Ventajas del constructivismo sentiente frente al constructivismo sensible.

El hecho de que en Kant la construcción matemática sea sensible, es fuente de insoslayables dificultades. Así ha tenido que verlo el propio Zubiri al reparar en el modo de "hacer sensiblemente" el objeto matemático. La cuestión que aquí nos planteamos es si el constructivismo sentiente supera la insuficiencia del constructivismo sensible de la matemática. Lo desarrollamos en los siguientes puntos:

1. La descripción que hace Zubiri del carácter sensible de la construcción kantiana (de la cual se apartará totalmente).

2. Las dificultades que conlleva entender de modo sensible el quehacer matemático.

3. Si es satisfactorio sostener dos tipos de "haceres matemáticos", el de Kant y el de Frege, sin una unidad ulterior.

4. Y, por último, se verá si el constructivismo sentiente de Zubiri supera las dificultades del constructivismo sensible, y si es válido como único fundamento del hacer matemático, tanto sensible como no sensible. Los puntos quedarán más bien esbozados, puesto que a lo largo de la tesis lo desarrollaremos de modo más exhaustivo.

 

1. ¿En qué términos se hace cargo Zubiri del modo kantiano de conceptuar el hacer matemático, para tomar distancia del mismo? En la exposición que hace del concepto de filosofía de Kant, — en su obra Cinco lecciones de filosofía —, insiste en el carácter sensible de la construcción recogiendo dos tesis kantianas:

a) Para que el objeto se nos muestre, tiene que aparecer sensitivamente. "No basta que la cosa sea real; es menester que sea sensible". [205] Zubiri constata el reduccionismo kantiano del termino "sentir", e implícitamente manifiesta su ampliación paradigmática (cfr. el punto "el sensismo de la matemática") desde sentir lo sensible (Kant) a sentir lo real. Es la diferencia entre el constructivismo sensible de la matemática y el constructivismo sentiente de la matemática.

b) Para hacer un objeto matemático sensible, tengo que construirlo en las formas a priori de la sensibilidad, espacio y tiempo, esto es en la intuición pura. "Tiempo y espacio son condiciones sensitivas mías que hacen posible que algo se me manifieste sensitivamente"[206]. Zubiri nos dirá, por el contrario, que sentir lo real exige construirlo en la impresión de realidad. Es la diferencia entre el idealismo transcendental del constructivismo sensible y el realismo transcendental del constructivismo sentiente.

En Kant, según la exposición zubiriana:

"Percibir es, por consiguiente, percibir algo como objeto. Y esto no depende de las cosas, sino de mí: la cosa se me manifiesta como objeto solamente si yo la hago, en forma sensitiva, objeto para mí. Este "hacer" sensiblemente objeto de algo es, pues, un hacer único que tiene dos aspectos. Por un lado es un hacer mío de carácter o forma sensible, y ello acontece en forma espacio-temporal, gracias precisamente a que espacio y tiempo son formas a priori de la sensibilidad. El hacer sensiblemente objeto de algo es hacerlo espacio-temporalmente. Pero por otro lado, este hacer es hacer sensiblemente un objeto."[207]

En efecto, el "hacer sensiblemente" el objeto matemático, descrito por Zubiri, responde a los textos kantianos.

"No podemos pensar una línea sin trazarla en el pensamiento, ni un círculo sin describirlo, como tampoco presentar tres dimensiones del espacio sin construir tres líneas perpendiculares a partir del mismo punto" [208]

2. Ahora bien: ¿Cómo nos representamos intuitivamente el espacio n-dimensional? ¿Cómo construimos los números transfinitos de la matemática de Cantor? ¿Cómo, si la construcción es a priori en la intuición pura, podemos construir distintas geometrías que incluso son incompatibles entre sí? ¿Cómo se explica la historicidad de los conceptos matemáticos? Teniendo presente que el paradigma de sentir es "sentir lo sensible", y que el constructivismo sensible es un idealismo transcendental, a nuestro modo de ver, no queda más salida que la de admitir la insolubilidad de estas cuestiones dentro del marco del constructivismo kantiano. Los caracteres que lo definen son: finitismo, ahistoricidad y unicidad. El superar estas limitaciones, determinó a Frege a buscar otro fundamento de la matemática no constructivo, sino lógico.

3. ¿Es satisfactorio, ante la limitación del constructivismo sensible, dividir el quehacer matemático en dos tipos radicalmente distintos?[209]. Ésta es la propuesta de Javier de Lorenzo:

"He tratado, hasta aquí, de mostrar algunos de los elementos de la Filosofía de la Matemática de Kant: problemática de esa Filosofía e intentos de solución de la misma. Y ello a través de unos rasgos que caracterizan un determinado tipo de hacer matemático: el figural-constructivo.

Pero también he indicado la existencia de otra línea, consecuente con la existencia de otro hacer matemático, el existencial-global, el que surge tras la ruptura epistemológica que se produce en el hacer matemático en los entornos de 1827. Otra línea que, entre otros, sistematizará Frege" [210]

El autor reconoce, pues, dos tipos de haceres matemáticos, con dos tipos distintos de fundamentación, a saber: 1. el constructivo-figural (el de Kant), y 2. el conjuntista existencial-global (el de Frege). Ninguno de ellos, nos dice, puede dar cuenta del quehacer total del matemático, pero no por ello debe limitarlo dogmáticamente a su dominio. No hay un fundamento único del quehacer matemático.

"Una vuelta a Kant permite reconocer, claramente, la validez del planteamiento de ambas líneas de pretendido fundamento del hacer matemático en sus campos propios, sin eliminaciones dogmáticas de uno en beneficio del otro.

Permite reconocer, a la vez, que dicho intento de fundamentación definitiva, de una vez para siempre, y en el que coinciden desde Kant a Frege, con Russell, Hilbert, Brouwer..., carece de sentido. Que sólo tiene sentido el intento de caracterizar, no fundamentar, cada una de las formas de la Matemática, cada uno de los aspectos en los que se manifiesta el uso constructivo de la razón pura" [211]

En este planteamiento de Javier de Lorenzo, nos parece que la cuestión de fondo es si el objeto matemático es sensible o lógico. Pues bien, según hemos visto en el texto, frente a las posturas exclusivistas, el autor admite un dominio matemático de objetos sensibles (de la que da cuenta Kant) y otro de objetos lógicos (de la que da cuenta Frege). Pero, aún delimitando los campos constructivo-figural y existencial-global, ¿encuentra cada uno de ellos una fundamentación adecuada en la filosofía de la matemática de Kant y de Frege, respectivamente? Si tenemos en cuenta, por una parte, que el Teorema de Gödel muestra insuficiente la caracterización lógica de la naturaleza matemática, y, por otra parte, que la construcción matemática, según la luz que arroja el análisis zubiriano, no es sintetizar sino más bien desplegar — porque lo que se llama "predicado" viene "exigido desde dentro de lo que se denomina "sujeto"—, entonces la respuesta es negativa.

4. ¿Supera el constructivismo sentiente las dificultades del constructivismo sensible? ¿ puede dar razón del hacer matemática tanto sensible-figurativo como existencial-global? Nos parece que, efectivamente, en el constructivismo sentiente de Zubiri no se plantean las dificultades del constructivismo sensible de Kant y, por otra parte, esta filosofía zubiriana de la matemática vertebra y fundamenta el tipo de "hacer matemático" tanto de Kant como de Frege. Justificamos seguidamente lo expresado.

Recordemos que la construcción sentiente no consiste en "hacer sensible" un contenido de un concepto sino en "hacer sentible", esto es, en proyectar, por postulación constructiva, el sistema de axiomas y postulados libremente creado, en la formalidad de realidad dada impresivamente por la aprehensión primordial. Este carácter permite conservar la ventaja fundamental del constructivismo sensible kantiano: la aplicabilidad de la matemática a la Ciencia de la naturaleza. Lo cual muestra que desde otro marco conceptual distinto al de Kant también es posible dar cuenta de ello y que, por tanto, no hay que aferrarse a los presupuestos kantianos, a fin de conservar esta ventaja del constructivismo sensible, como parece sugerir Javier de Lorenzo en el siguiente texto.

"Una enorme ventaja, la de la epistemología kantiana, concretada a este aspecto [la aplicabilidad de la matemática a la Ciencia de la naturaleza]. Ventaja que, sin embargo, se vuelve radicalmente problemática si se rechaza su punto de partida, el de la constitución del sujeto cognoscente en esas dos facultades así como su rechazo a que pueda alcanzarse el conocimiento en sí de las cosas; si se rechaza su giro copernicano por el que serán las cosas las que se regulen por el conocimiento y no sea el conocimiento el que quede regulado por las cosas" [212]

Zubiri, desde el constructivismo matemático, rechaza uno por uno cada presupuesto kantiano:

1. Que el sujeto cognoscente tenga dos facultades; sólo tiene una: inteligencia sentiente.

2. Que el objeto de la matemática sea ideal; es real, si bien postulada y transcendental, y no "en sí" y transcendente (lo trataremos en el próximo capítulo)

3. Y el giro copernicano: el conocimiento regula las realidades matemáticas; es la realidad actualizada la que nos impone toda el movimiento y la marcha intelectiva.

Precisamente el nuevo marco del sistema zubiriano permite que el constructivismo sentiente explique la aplicabilidad de la matemática a la Ciencia de la naturaleza. La razón de ello estriba en que la libre construcción de la inteligencia matemática sólo es posible por un principio real de las cosas mismas. En el caso de las geometrías, el principio real que permite la libre construcción de los espacios geométricos es la espaciosidad. Ésta es un principio real de las cosas que posibilita tanto la libre construcción del espacio geométrico, como la libre movilidad de los cuerpos que determina el espacio físico. El principio real del espacio físico y del espacio geométrico es el mismo: la espaciosidad. De ahí el isomorfismo entre ambos. Dicho de otro modo, al ser la matemática una construcción en la impresión de realidad, la construcción tiene un momento de fuerza de imposición de la realidad, lo que constriñe a la razón para que no sea arbitraria e infundada y pueda tener aplicación a la realidad.(lo veremos más detalladamente en el capítulo siguiente).

Una vez señalada que la ventaja del constructivismo sensible de Kant la tiene también el constructivismo sentiente de Zubiri, en cuanto que ambos son constructivismos (a diferencia del logicismo de Frege), pasamos a la problemática del constructivismo sensible para esbozar su solución dentro del constructivismo sentiente.

a) Problema del singular y el universal.

En el constructivismo sensible es preciso el recurso a lo que Kant denomina esquema como intermediario entre la intuición y el concepto. La problemática del esquematismo es numerosa. En el constructivismo zubiriano no se trata de homogeneización de los contenidos intuitivo y conceptual, esto es, de dar un contenido intuitivo al concepto, sino que se trata de que el contenido conceptual al realizarlo en la impresión de realidad, queda en formalidad de realidad, o "de suyo". Por tanto el hacer sentiente el concepto no es sino hacerlo realidad (contenido "de suyo"). No sentimos el contenido matemático sensiblemente, pero sentimos que es "de suyo", real. La problemática que se plantea en el constructivismo sensible entre la singularidad del contenido intuitivo sensible y la universalidad del objeto matemático no se plantea en el constructivismo sentiente porque es unidad entre intuición y concepto en la línea de la formalidad, y no es síntesis en la línea del contenido.

b) El problema de la historia en la matemática.

Las definiciones matemáticas, según Kant, nos proporcionan conceptos constructos "acabados". Para Zubiri no. Los juicios matemáticos, según Kant, son necesarios y universales; mientras que para Zubiri dependen de la realidad postulada, si ésta cambia los juicios matemáticos cambian también. El constructivismo sensible de la matemática es ahistórico, no así el constructivismo sentiente que es histórico. El carácter histórico se inscribe en el carácter sentiente de la razón misma. Desarrollaremos este punto en el capítulo de la verdad matemática.

c) El problema de la pluralidad de teorías matemáticas.

El grave problema del constructivismo sensible reside en su idealismo transcendental. Desde éste, el espacio y el tiempo son formas a priori de nuestra sensibilidad, estructuras del sujeto transcendental que hacen posible la experiencia. Pero dado que las estructuras no varían, ¿cómo es posible la pluralidad de geometrías no-euclídeas? No cabe sino responder que son construcciones lógicas, pero no sensibles y, consecuentemente, no son conocimiento de realidad matemática. El constructivismo sensible construye un contenido unívoco no plural, por ejemplo sólo una geometría es válida (para Kant, la geometría euclídea es la estructura del espacio). Sin embargo, la construcción sentiente posibilita la construcción de sistemas de axiomas y postulados alternativos, porque no se apoya en el contenido sino en la formalidad de realidad. El constructivismo sentiente, según analizaremos en el siguiente capítulo, es un realismo transcendental. Las construcciones sentientes de los distintos espacios geométricos son libres construcciones fundadas en la realidad transcendental, en la espaciosidad. No son meras posibilidades lógicas, son posibilidades reales.

d) El problema de los dominios infinitos de funciones matemáticas.

El constructivismo sensible exige la construcción intuitiva-sensible del contenido de los objetos matemáticos. Pero ¿puede representarse intuitivamente el contenido del infinito actual, del continuo, o de cualquier función de dominio infinito? Es evidente que no. El constructivismo sensible es, pues, un finitismo; como lo es también el constructivismo de Brouwer, y el constructivismo ruso, por ejemplo de Markov. Kant concede al infinito actual el estatuto de una Idea; mientras que el infinito potencial es admisible como proceso de construcción iterativa. Esta limitación kantiana lleva a Javier de Lorenzo a reforzar su distinción entre dos tipos de matemáticas: la constructiva -finitista- y la conjuntista-existencial -infinitista.

"...hay dos matemáticas diferentes, una de carácter finitista, figural y constructiva, y otra de carácter existencial, global, infinitista.

Y desde esta posición es desde la que cabe considerar a Kant como uno de los primeros pensadores y sistematizadores de la Matemática finitista, constructiva, mientras que corresponde a Frege, entre otros, la sistematización y problematización del otro tipo de hacer, existencial, global" [213]

Esta división, desde el constructivismo sentiente, creemos que no tiene razón de ser. El constructivismo sentiente, a diferencia del sensible, no requiere sentir el contenido del continuo o infinito actual para poder realizarlo sentientemente en la impresión de realidad. La construcción matemática es un proceso sentiente en la línea de la formalidad, no del contenido. El constructivismo sentiente es, por tanto, un infinitismo (lo desarrollamos en el próximo capítulo). Dice Zubiri:

"Sólo una inteligencia sentiente puede por ejemplo no sentir el contenido de un conjunto continuo, esto es el conjunto de los números irracionales, y sin embargo realizar libremente este contenido (conceptuado sea por meras definiciones, sea por operaciones ejecutadas) de un modo sentiente" [214]

Construir algo sensiblemente es hacerlo espacio-temporal. El infinito actual ¿es espacio temporal? No. Pues no es fenómeno, no se puede construir sensiblemente. Ahora bien, Zubiri considera que construir algo sentientemente es hacerlo real, inscribirlo en la impresión de realidad; la pregunta es distinta: ¿es el infinito actual "de suyo"? Sí, pues es una construcción sentiente. No tenemos impresión sensible porque el contenido no se nos da impresivamente, sino que es construido en la impresión transcendental de la realidad campal. Del infinito actual tenemos impresión transcendental. Su existencia es postulada en "la" realidad. Lo mismo puede decirse del Axioma de elección de Zermelo. Por tanto, el constructivismo sentiente es un enfoque global-existencialista y funcional, del mismo modo como lo es la matemática infinitista-existencial de Frege y Russell[215], y, además, tiene la ventaja, sobre esta concepción logicista, de su conformidad con las exigencias del Teorema de Gödel. La construcción matemática siempre es sentiente, a lo cual puede añadirse en algunos casos el carácter sensible, pero éste no es una condición para todos los objetos matemáticos. De ahí que pueda dar razón de los dos tipos de haceres matemáticos, sea el de Kant o el de Frege.

El análisis anterior, arroja la conclusión de la insuficiencia de la filosofía "concipiente" o "sensible" de la matemática adoptada por Kant (también la de Frege), y apoya la tesis que mantenemos de la fundamentalidad de la filosofía sentiente de la matemática: ésta funda la filosofía intuicionista de la matemática, la filosofía racionalista de la matemática y la filosofía sintética de la matemática. Y, a la vez, arroja luz sobre su relación, que no es de contraposición, sino que podríamos decir, por seguir el paralelismo con los modos de intelección, que hay unidad de despliegue entre las distintas filosofías concipientes de la matemática.

Si la función del filósofo es unificar la realidad y unificar la intelección, allí donde hay ruptura —según el espíritu hegeliano—, Zubiri cumple perfectamente esta misión, en general, y, como acabamos de ver, en la filosofía de la matemática. Si Hegel decía que la filosofía kantiana partía del entendimiento y por eso consideraba los elementos aislados y estancos, y que para superar esta división había que elaborar la filosofía desde la razón absoluta; Zubiri afirma que toda la tradición filosófica se construye desde la dualidad sentidos e inteligencia, y de ahí todas las divisiones epistemológicas u ontológicas, y para su superación hay que partir de la unidad radical de inteligencia sentiente. Mientras que el primero identifica la diversidad y por tanto absolutiza, el segundo unifica pero no identifica: la unidad en el constructivismo sentiente del intuicionismo y del racionalismo está en la línea de la formalidad, pero no en la línea del contenido; y en la línea de la intelección sentiente, pero no en los modos de intelección.

Por último, no podemos pasar por alto la repercusión del análisis de la filosofía matemática en el pensamiento total de Kant y de Zubiri. Ambas filosofías de la matemática están incardinadas y son piedras de toque de sus concepciones filosóficas globales. Entonces, ¿la superioridad del constructivismo sentiente de la matemática no implica la superioridad de la filosofía entera de Zubiri? No estamos diciendo que la filosofía de Kant sea errónea sin más, no es cuestión de error y de verdad, sino de mayor aproximación explicativa, y esto sólo se consigue dando un brinco desde las posibilidades legadas por otros (este sentido da también Zubiri a la historia). Sin el constructivismo sensible de Kant es posible que el constructivismo sentiente de Zubiri no sería. El haber experimentado su choque con la nueva matemática, ha sido fuente de nuevas sugerencias. Así entendemos (Zubiri y nosotros) la dialéctica del pensamiento de la humanidad. Nada se piensa ex nihilo, sino desde las cosas y desde el bagaje cultural de nuestro tiempo. Desde nuestro punto de vista, las sugerencias de la matemática gödeliana y el constructivismo sensible de la matemática de Kant han dado qué pensar a Zubiri, y su respuesta ha sido de gran fecundidad, empezando por su concepción de la matemática.

 

3.1 4 Matemática y Filosofía: ¿Dos usos de la razón o dos órdenes de lo real?

Kant, en la II parte de la Crítica de la Razón Pura, en la "Doctrina transcendental del método", hace una serie de reflexiones en torno a la Matemática y la Filosofía, que nos parece que hay que replantear a la luz del pensamiento de Zubiri. Las cuestiones claves a discutir son: ¿Tiene la razón pura dos usos distintos, a saber, un uso transcendental y un uso constructivo? ¿Corresponde el primero a la Filosofía y el segundo a la Matemática? ¿Procede la Filosofía discursivamente frente a la Matemática que lo hace intuitivamente? ¿Tiene la Filosofía que considerar lo universal en abstracto? ¿Consiste la solidez de la Matemática en sus definiciones, axiomas y demostraciones? ¿Es el método matemático impracticable para la filosofía? ¿Tiene la Filosofía un valor meramente negativo, de tal modo que no amplía nuestro conocimiento?

Todas estas cuestiones podemos sintetizarlas en un problema sumamente actual: la demarcación entre Matemática y Metafísica (en términos más generales, entre Ciencia y Filosofía). La respuesta pende de qué se entienda por metafísica y de qué se considere su objeto. Y esto, a su vez, viene determinado por la noción que se tenga de inteligencia, si es sensible (concipiente) o sentiente. Lo vamos a constatar en la confrontación de Kant y Zubiri. El hecho de que Kant parta de la inteligencia sensible o concipiente le lleva a una concepción concipiente de la metafísica y de su objeto, y, por tanto, a una demarcación concipiente entre Matemática y Metafísica. Por el contrario, Zubiri alumbra, desde la inteligencia sentiente, una concepción sentiente de la metafísica y de su objeto, y, consecuentemente, establece una demarcación sentiente entre Matemática y Metafísica.

3.1.4.1 Kant: uso discursivo (Metafísica) y uso constructivo (Matemática) de la razón

Kant comienza rechazando la distinción habitual entre matemática y filosofía según su objeto o materia. Mientras el objeto de la matemática se consideraba que era la cantidad, el objeto de la metafísica era la cualidad. Esto no es correcto para el autor, porque la filosofía se ocupa también de magnitudes, por ejemplo la totalidad, la infinitud; y, asimismo, las matemáticas pueden ocuparse de cualidades, por ejemplo la continuidad de la extensión. Por tanto, la diferencia hay que buscarla en el modo de tratar la razón el objeto aún cuando sea común. Matemática y Metafísica, dice Kant, son dos usos de la razón pura:

1. El uso derivativo o discursivo de la razón pura, que procede por derivación de meros conceptos, es el conocimiento filosófico. Para Kant, la metafísica (o filosofía) es un conocimiento racional derivado de conceptos. De ahí que sea una disciplina de índole abstracta, sin ningún apoyo empírico ni intuitivo. La metafísica discurre a priori, a través de conceptos abstractos y universales, con lo cual no hay ningún modo de confirmar la realidad de esos conceptos. Con sus palabras:

"la filosofía pura, en cambio, trata de solucionar los problemas de la naturaleza con conceptos discursivos a priori, sin poder hacer intuible a priori, ni, por tanto, confirmar, la realidad de esos conceptos" [216]

2. El uso constructivo de la razón pura, que procede por construcción de conceptos en la intuición pura, es el conocimiento matemático. La matemática es, pues, un conocimiento obtenido por construcción de los conceptos. Ya hemos visto en el análisis de su filosofía matemática, el constructivismo sensible, que el objeto matemático no es mero concepto o producto de la razón, sino que es una construcción de índole sensible, y que construir un concepto significa presentar la intuición a priori que le corresponde. Con este enfoque de la matemática Kant se aparta de la tradición racionalista.

Tanto la noción de metafísica como, consecuentemente, el criterio kantiano de demarcación de la matemática, es propio de la inteligencia sensible o concipiente. Transcribimos un texto básico que pone de manifiesto este punto de partida.

"Sin embargo, por más que en estos casos filosofía y matemáticas tengan un objeto común, su modo de tratarlo mediante la razón es completamente distinto en una y otra ciencia. La primera se atiene sólo a conceptos universales, mientras que la segunda nada puede hacer con el simple concepto, sino que va inmediatamente en pos de la intuición, en la cual considera el concepto en concreto, pero no empíricamente, sino sólo en una intuición que representa a priori, es decir, que ha construido y en la que aquello que se sigue de las condiciones universales de la construcción tiene que ser también universalmente válido respecto del objeto del concepto construido"[217]

Kant recurre al concepto de triángulo para ejemplificar la gran diferencia que existe entre el uso discursivo de la razón, que opera por conceptos, y el uso intuitivo de la misma, que opera por construcción de conceptos; es decir, entre el procedimiento metodológico que sigue el filósofo y el matemático. ¿Qué hace el primero con el triángulo? Se pone a filosofar, esto es, a pensar discursivamente sobre el concepto de triángulo; analiza los conceptos de triángulo, línea recta, de ángulo o de tres. Pero con ello no consigue ampliar el conocimiento más allá de sus definiciones, su esfuerzo es inútil. ¿Y qué hace el matemático con el triángulo? Él no se pone a pensar discursivamente, sino que inmediatamente actúa, construye intuitivamente un triángulo, prolonga un lado del triángulo y comprueba la relación de los ángulos adyacentes, divide el ángulo externo y ve la relación entre un ángulo adyacente externo y uno interno... y así sucesivamente. De este modo, el matemático, que marcha por el seguro camino de la intuición, llega a una solución evidente y universal del problema.

Tras esta caracterización de la matemática y de la metafísica, según los usos que le son propios de la razón, Kant pasa a comparar sus métodos. Le preocupa que la metafísica, deslumbrada por el éxito de las matemáticas, trate de imitar el método de esta ciencia. ¿Es esto posible? De ningún modo, nos dirá el autor. Las matemáticas gozan de un estatuto de certeza, de apodicticidad, que se debe a su peculiar método. Sus definiciones, axiomas y demostraciones no pueden llevarse a cabo en la metafísica. Si la matemática usa el método filosófico, se convierte en "pura palabrería"; y si la filosofía emplea el método matemático genera "castillos de naipes". Dice Kant:

"La solidez de las matemáticas se basa en definiciones, axiomas y demostraciones. Me limitaré a mostrar que ninguno de estos elementos puede ser, en el sentido en que los toman las matemáticas, ni suministrado ni imitado por la filosofía; que, siguiendo su método propio, el geómetra no puede dar lugar en filosofía más que a castillos de naipes; que el filósofo, siguiendo el suyo, no puede producir en matemáticas otra cosa que palabrería. No obstante, la filosofía consiste en conocer sus propios límites"[218]

Kant va a ir examinando cada aspecto del método matemático —definiciones, axiomas, demostraciones— e indica la razón de su impracticabilidad para la filosofía. Veamos.

1. Definiciones. Los únicos conceptos que pueden ser definidos son los matemáticos, porque sus conceptos contienen una síntesis arbitraria que puede construirse a priori. Las definiciones matemáticas, en tanto que construcciones originarias, no contienen ni más ni menos propiedades que lo que encierra el concepto; son, por tanto, completas. Esto nunca ocurre en la filosofía, que más que definir (presentar algo dentro de sus límites) lo que hace es explicar. En la matemática las definiciones son el punto de partida, mientras que en la filosofía es el punto de llegada. (El error de esta interpretación kantiana de los conceptos matemáticos, se pondrá de manifiesto en el capítulo de la historicidad de la verdad matemática)

"En efecto, esta ciencia [la matemática] representa a priori, en la intuición, el objeto que piensa, y es seguro que éste no puede contener ni más ni menos que el concepto, ya que el último ha sido ofrecido por la definición de modo originario, es decir, sin derivar esta definición de otra cosa... las definiciones filosóficas no son más que exposiciones de conceptos dados, mientras que las definiciones matemáticas son construcciones de conceptos producidos originariamente"[219].

2. Axiomas. Kant los define como principios sintéticos a priori inmediatamente ciertos. Esta certeza es debida a su carácter intuitivo. Esto en la matemática es posible, mientras que en la filosofía es imposible porque sus proposiciones son síntesis de meros conceptos, exentas de intuición, y, por tanto, nunca pueden ser inmediatamente ciertas.

"Los principios discursivos son, pues, algo completamente distinto de los intuitivos, es decir, de los axiomas. Los primeros requieren siempre una ulterior deducción; los segundos pueden prescindir totalmente de ella y por eso son evidentes, cualidad que jamás pueden arrogarse los principios filosóficos, por muy ciertos que sean. De ahí que una proposición sintética de la razón pura trascendental se halle a infinita distancia (contra lo que se suele afirmar con obstinación) de una evidencia como la de la proposición "Dos y dos son cuatro’" [220]

Digamos, ahora meramente de paso, que estas afirmaciones de Kant son todas muy cuestionables: ¿son las evidencias matemáticas apodícticas ?, ¿se debe este carácter al método peculiar de la matemática?, ¿carecen de evidencia los juicios metafísicos?, ¿es la certeza de carácter intuitivo?... Responderemos estas cuestiones, desde la perspectiva zubiriana, en el capítulo de la verdad del logos.

3. Demostraciones. Kant reserva el nombre de demostraciones para la matemática, pues es preciso proceder por intuición del objeto, y ésta no se da en las proposiciones filosóficas. Para la filosofía prefiere darle el nombre de pruebas acroamáticas (discursivas), esto es, que se realizan por simples palabras. Es la diferencia entre el método matemático, como vía en la intuición, y el método filosófico, como vía en el pensamiento.[221] Es notoria la concepción concipiente de la metafísica, defendida por el autor. En sus palabras:

"En consecuencia, sólo las matemáticas poseen demostraciones, debido a que su conocimiento no deriva de conceptos, sino de la construcción de los mismos, es decir, de la intuición que puede darse a priori en correspondencia con los conceptos. El mismo procedimiento del álgebra, con sus ecuaciones, a partir de las cuales, por reducción, produce la verdad juntamente con su prueba, aunque no es una construcción geométrica, es una construcción característica por la cual se presentan en la intuición los conceptos a través de signos, especialmente los que se refieren a relaciones de magnitud" [222]

Kant hace la distinción en las proposiciones apodícticas, entre dogmata y mathemata. Las primeras son atribuibles a la filosofía y las segundas sólo a la matemática. Son juicios dogmáticos los formados por meros conceptos, a diferencia de los juicios formados por construcción de conceptos.

"Divido todas las proposiciones apodícticas (tanto las demostrables como las inmediatamente ciertas) en dogmata y mathemata. Una proposición sintética directamente extraída de conceptos es un dogma, mientras que una del mismo tipo, pero formada por construcción de los conceptos, es un mathema. (...) de las dos clases de proposiciones sintéticas a priori sólo pueden llamarse dogmas las pertenecientes al conocimiento filosófico. Difícilmente podría darse este nombre a las proposiciones de la aritmética o de la geometría" [223]

La filosofía, como mera especulación, más que extender nuestro conocimiento (como sí hace la matemática), tiene una función negativa: sirve para evitar errores. Esta es la conclusión a la que quiere llegar Kant.

3.1.4.2 Zubiri: orden transcendental (Metafísica) y orden talitativo (Matemática y Ciencia) de la realidad.

El planteamiento sentiente de Zubiri sobre la metafísica y su demarcación de la matemática (y de la ciencia en general) es muy distinto del planteamiento sensible o concipiente , que acabamos de ver en Kant. La diferencia entre Matemática y metafísica no está, según Zubiri, en dos usos distintos de la razón. Y, además, es un grave error considerar la metafísica como el uso discursivo o derivativo de conceptos de la razón. Dado que la razón es constitutivamente sentiente no puede hablarse de un uso discursivo y un uso intuitivo de la misma. Hay, si se quiere, un uso sentiente, tanto si se trata de la matemática como si se trata de la metafísica. El acto único de la inteligencia sentiente es la impresión de realidad. En ella se mueve siempre la razón. El no haberlo visto así es lo que ha llevado a Kant a abrir un abismo entre Matemática y Metafísica, con unas consecuencias nefastas para ésta. De ahí la importancia en insistir en el carácter sentiente de la razón.

¿Cuál es la demarcación sentiente entre Metafísica y Matemática? Ambas tienen por objeto la realidad dada impresivamente, pero según una dimensión distinta. La Matemática, como el resto de las ciencias, se ocupa de la dimensión talitativa de lo real, mientras que la metafísica se ocupa de la dimensión transcendental de lo real. Ninguna de estas dos dimensiones de la realidad pueden darse independientemente de la otra. Así el carácter transcendental-inespecífico de la realidad no es nada que exista en un orden distinto al talitativo-específico, ni que se "dé" de suyo, sino algo esencialmente fundado en una realidad de determinada talidad y que sólo puede darse en unidad con ésta. Esta unidad del "dato de realidad" queda expresada en lo que Zubiri denomina "impresión de realidad". En Zubiri, la división clásica entre mundo sensible y mundo inteligible no se da porque no hay separación entre sentir e inteligir: la inteligencia es sentiente. Esto es fundamental. Dice Zubiri:

"La cosa real puede considerarse desde dos puntos de vista. Ante todo desde el punto de vista de sus notas reales. Entonces considero la cosa tal y como es. Es el punto de vista de las notas de su talidad, objeto de la ciencia positiva en el más amplio sentido del vocablo. Pero estas notas no sólo son tales como son, sino que por pertenecer "de suyo" a la cosa constituyen lo que ella "de suyo" es, es decir, constituyen "su" realidad ... desde el punto de vista de los caracteres de ‘su’ realidad, tendremos no una ciencia positiva sino una metafísica." [224]

Veamos a continuación las características de estos dos órdenes de la realidad que determinan el objeto de la matemática y de la metafísica.

1. El orden de la talidad: cada cosa es tal o cual determinada. Es el contenido específico de la cosa real. La talidad se puede considerar según dos aspectos: según aquello que ella es en sí misma, y según aquello que transcendentalmente determina. Y esto último lo denomina Zubiri "función transcendental", es la función por la que la talidad determina las propiedades trascendentales de la realidad. La matemática y las ciencias estudian las cosas y sus relaciones desde el punto de vista de sus notas reales, de su talidad.

2. El orden trascendental: la realidad en cuanto realidad. A diferencia de Kant, nuestro autor considera que la transcendentalidad no es un orden separado de conceptos, "más allá" de lo real, sino que, por el contrario, es una dimensión tan física como la talitativa. Tampoco debe entenderse como un orden yuxtapuesto al de la talidad, pues "realidad" es un carácter que trasciende a todos los momentos, modos y diferencias de la talidad de lo real, bien entendido que dentro de la aprehensión de realidad. La trascendentalidad compete en primer lugar al carácter inespecífico de realidad, no a un concepto universal. El trans no es un carácter conceptivo de las cosas reales, sino es un momento físico de las cosas reales en cuanto sentidas en impresión de realidad. Ciertamente, no es lo físico del contenido, mas es lo físico de la formalidad. Por tanto, según Zubiri, el "trans" no es un trans de lo físico, sino lo "físico mismo como ‘trans". La trascendentalidad no es comunidad conceptiva sino comunicación real. Kant, al igual que la filosofía griega y medieval, nos dice Zubiri, parte de una concepción concipiente de la metafísica, se ha fijado en la línea del contenido. De ahí que conceptúe el objeto de la meta-física como lo ultra-físico, o lo transcendente. [225].

Y es que, efectivamente, esto que se ha llamado el orden transcendental, aquello en que la realidad consiste, se piensa que es por lo menos el correlato de un concepto muy abstracto. Ahora bien, esto es falso. No que este concepto no existe —bien entendido. Pero formaliter, el orden transcendental, la función transcendental, no es el correlato de un concepto: es la estructura real de las cosas qua reales. Es precisamente el modo de realidad que su talidad determina en cada una de ellas."[226]

Desde la inteligencia sentiente, el orden transcendental no es lo transcendente, no tiene un carácter a priori, como pretende Kant y en general toda la Filosofía clásica. No es un orden anterior a las cosas que son reales. No hay más realidad, dice Zubiri, que la realidad de cada una de las cosas[227]. Lo transcendental es algo dado en impresión. Esta conceptuación sentiente de lo transcendental (como ya anunciábamos en el capítulo anterior) tiene una honda repercusión en todo el planteamiento que venimos haciendo de la demarcación entre matemática y metafísica. Al ser algo dado en impresión, lo transcendental no está concluso y cerrado, sino que tiene un carácter abierto y dinámico.

"...lo metafísico es el orden de lo real en cuanto real, esto es, el orden de lo transcendental. Ahora bien, lo transcendental no es algo concluso y a priori; es algo dado en impresión (impresión de realidad), y es algo abierto, y abierto dinámicamente. Las verdades metafísicas son sólo estadios de la marcha intelectiva hacia la verdad de la realidad"[228]

El alcance filosófico de considerar que el objeto de la metafísica es algo dado en impresión es enorme; se deja sentir, en primer lugar, en la alteración respecto de la concepción kantiana de cuál es el método metafísico.

Desde la inteligencia sentiente, no hay que temer que la metafísica discurra por un carril generador de extravagancias e ilusiones erróneas, más de lo que pueda ocurrirle a la matemática. La vía metafísica no es el pensamiento, sino la impresión transcendental. No sólo la matemática parte de una intelección constructiva de conceptos, la mayoría de conceptos científicos, según veíamos en el capítulo anterior, son construidos a partir de las notas abstractas de lo empírico. Pero son construcciones en "la" realidad aprehendida. La filosofía, según Zubiri, es ciencia y saber de lo real. El no poder dar definiciones completas en filosofía se debe a la apertura de la realidad y de la intelección (en cuanto actualización de la realidad), lo cual ocurre también en la propia matemática (Teorema de Gödel). Por otra parte, los juicios metafísicos no son menos evidentes y ciertos que los matemáticos. Todo juicio, lo veremos más adelante, es evidente porque la intelección de lo que algo es "en realidad" viene exigido por la realidad aprehendida impresivamente. Y, por último, las demostraciones metafísicas no son un discurrir lógico en los conceptos a priori (ni pura palabrería), sino que son una marcha en la impresión de realidad, en la que si bien la razón crea libremente el contenido profundo de la realidad, sin embargo lo hace desde la fuerza coercitiva con que se le impone la realidad aprehendida sentientemente. El resultado no es, usando una figura kantiana, "sólo un paso ligero cuyas huellas quedan completamente borradas por el tiempo", sino distintos estadios de la marcha de la razón sentiente hacia la verdad de la realidad. La metafísica es ciencia y saber de la realidad en cuanto realidad.

Al estar determinado el orden transcendental por la función transcendental que tienen las talidades, no se puede saber de un modo definitivo, por el contrario la razón tiene epagógicamente que ir descubriendo penosa y largamente a lo largo de la investigación.[229] No existe una metafísica general, sino una metafísica como ciencia y saber del orden transcendental, de carácter intramundana. La función transcendental es, pues, la pieza clave para conceptualizar la demarcación sentiente entre matemática y metafísica. La talidad matemática en función transcendental determina una aspecto de la realidad en cuanto realidad.

"Entonces se preguntará dónde queda la Metafísica general. Yo contestaría que no queda en ninguna parte. Porque la Metafísica general no existe. No existe nada más que la Metafísica como ciencia y como saber del orden transcendental. Y lo que se llama Metafísica general sería el ver la realidad en tanto que procedente de Dios y de una causa primera. Pero esto es una consideración completamente extramundana" [230]

Zubiri lleva a cabo el proceso de la reificación y sensibilización tanto de la matemática como de la metafísica, y esto es sólo posible desde la conceptualización de la inteligencia sentiente. Ni la matemática ni la metafísica son meros sistemas de conceptos: el objeto de ambas es la realidad. La ciencia o el saber siempre es de realidad, la única distinción es en cuanto realidad positiva (atendiendo al contenido real) o en cuanto metafísica (atendiendo a la estructura última de la formalidad de realidad). A este resultado le ha conducido la crítica radical de la dualidad del inteligir y del sentir, esto es, la inteligencia sentiente. Para Zubiri realidad es un concepto de inteligencia sentiente, mientras que para Kant es un concepto de inteligencia concipiente. Estas perspectivas zubiriana y kantiana originan distintas demarcaciones entre matemática y metafísica.

En el capítulo cuarto, dedicado al realismo matemático, nos referiremos al fundamento metafísico de la matemática. El constructivismo sentiente no tiene como fundamento el sujeto transcendental (como el constructivismo sensible) sino la realidad transcendental. De ahí que le denominaremos, desde el punto de vista del objeto, Constructivismo Transcendental. Tenemos impresión de realidad que como tal no es sensible sino, como vimos en el ‘sensismo de la matemática’, es impresión transcendental o impresión intelectiva. Este es el objeto metafísico y la base sobre la que el matemático postula constructivamente sus objetos. La matemática tiene su raíz, pues, en el suelo de la Metafísica. Y viceversa, también los contenidos de la matemática tienen una determinación transcendental.

 

3.2. Necesidad de "realizar" los conceptos objetivos de la construcción axiomática-formalista.

A fin de contextualizar la interesante aportación del constructivismo sentiente de la matemática respecto a la noción "conceptiva" de construcción que manejan tanto Gödel como Cohen —en la axiomatización formalista de la teoría de conjuntos—, presentamos a continuación una breve introducción histórica de la significación matemática de los conjuntos construibles de Gödel y de los conjuntos no-construibles de Cohen.

El problema planteado en la teoría de conjuntos axiomatizada según los axiomas de Zermelo-Fraenkel es si la hipótesis del continuo de Cantor y el axioma de elección de Zermelo son verdaderos o falsos. Pues bien, entre Gödel y Cohen probaron la independencia tanto del axioma de elección como de la hipótesis del continuo respecto de los demás axiomas.

En 1938 Gödel, tomando como base la teoría axiomática de Zermelo-Fraenkel, demostró que si la teoría de conjuntos restringida es consistente, entonces también lo es la teoría de conjuntos típica. El axioma de elección no es más peligroso que los otros axiomas. Y respecto a la hipótesis del continuo de Cantor, Gödel demostró que si la teoría de conjuntos restringida más la hipótesis del continuo implica una contradicción, ésta se dará en la teoría de conjuntos restringida. Así probó la consistencia relativa de la teoría de conjuntos típica respecto a la teoría de conjuntos restringida. La hipótesis del continuo no puede demostrarse que es falsa. Gödel construyó un nuevo modelo para probar la consistencia de la teoría de conjuntos tanto restringida como la típica y no típica. Es el modelo de "conjuntos constructibles". Dentro del campo de los conjuntos constructibles, el axioma de elección y la hipótesis del continuo pueden ser demostradas. En la teoría ordinaria (no necesariamente constructible) de conjuntos no se han demostrado ni el axioma de elección ni la hipótesis del continuo. Cualquiera podría ser aceptado sin generar contradicción a menos que los axiomas "seguros" de la teoría de conjuntos restringida fuesen ya contradictorios. Cualquier contradicción de origen ha de estar ya presente en la teoría de conjuntos constructibles, que es un modelo para la teoría de conjuntos ordinaria.

En 1963 Cohen, discípulo de Gödel, demostró que si a la teoría típica (cantoriana) se le añade la negación de la hipótesis del continuo de Cantor no se genera contradicción. Igualmente, si se añade la negación del axioma de elección es consistente. De este modo la hipótesis del continuo y el axioma de elección no son demostrados como ciertos, por tanto serían falsos. Cohen toma como modelo los conjuntos constructibles de Gödel a los que se añade al menos un conjunto no-constructible. Todo conjunto constructible tiene un carácter específico: los pasos por los cuales ha sido construido. El conjunto no-constructible tiene un carácter genérico, carece de individualidad. Sólo si esto es posible existe esperanza de negar el axioma de elección o la hipótesis del continuo. Podríamos negar el axioma de constructibilidad puesto que Gödel demostró que la constructibilidad implica el axioma de elección y la hipótesis del continuo, esto es el primer paso a fin de negar cualquiera de estas dos proposiciones.

El propio Zubiri, para esclarecer la ultimidad de su noción sentiente de construcción matemática, analiza qué se está entendiendo por construcción en los conjuntos construibles de Gödel y en los conjuntos no-construibles de su discípulo Cohen, y en qué difiere del sentido que tiene en su filosofía de la matemática. Gödel llama construir un conjunto sobre la base de los axiomas de Zermelo-Fraenkel a generarlo a través de la aplicación iterada de ciertas operaciones axiomáticamente definidas. Partiendo de esta noción, Cohen dice que los conjuntos no-construidos son los que sólo tienen propiedades genéricas en virtud de las cuales forman un conjunto, pero carecen de individualidad o especificidad, ahora bien "forzarán" a las propiedades genéricas a especificarse. Zubiri hace la observación de que aunque parezca contradictorio la existencia, según Cohen, de conjuntos no-construibles y su afirmación de que "todo lo matemático es construido", ésta es mera apariencia porque no tienen la misma noción de construcción, y se pregunta ¿qué es en el fondo lo que construyen Gödel y Cohen? A lo cual responde:

"Lo que Gödel y Cohen construyen es en el fondo el concepto objetivo tanto específico como genérico. Pero en cambio la construcción a que yo me refiero consiste en realizar ante mi inteligencia un concepto ya construido objetivamente (tanto si es construible como si no lo es). Y en este sentido la realización misma puede y debe llamarse construcción. Es pues algo muy distinto de la construcción en el sentido de Gödel y Cohen. Tanto los conjuntos construibles como los no-construibles están construidos en el sentido de realizados ante mi inteligencia."[231]

La línea de construcción de los conjuntos matemáticos tanto en Gödel como en Cohen es concipiente. Según vimos en el punto del constructivismo matemático, construcción en sentido concipiente es conceptualizar. Y el resultado de esta construcción en tanto que concipiente es un concepto objetivo. Piensa Zubiri que si esto fuera así, entonces se trataría de lo que el conjunto "sería" y la matemática se ocuparía de conceptos objetivos, pero no de realidades, es decir, de conjuntos que son. Esta construcción conceptiva del axiomatismo formalista de Gödel y Cohen es, por tanto, radicalmente insuficiente. Construir no es sólo crear un contenido intencional e irreal sino que es preciso proyectar este contenido del concepto sobre "la" realidad "según conceptos".

Por el contrario, desde la inteligencia sentiente, construir recordemos que no es conceptualizar sino realizar ante la inteligencia, en la impresión de realidad dada en aprehensión primordial pero liberada de un contenido concreto, un concepto ya construido objetivamente (sea construible o no-construible, esto es, genérico o específico), como su contenido. Se trata de la construcción según conceptos del contenido de la realidad "físicamente" dada. Lo postulado no es la verdad lógica sino, como ya indicamos, es el contenido de la realidad. Es toda la diferencia entre la noción de construcción conceptiva de Gödel y Cohen, y la construcción sentiente de Zubiri. Es muy significativo el texto de Zubiri:

"los conjuntos de Gödel y Cohen están construidos (en mi concepto de construcción) en la realidad física. Entonces la construcción misma no concierne formalmente a los conceptos, no es una construcción "conceptiva" sino que es una realización en ‘la’ realidad física, pero ‘según conceptos; dos cosas completamente distintas."[232]

En definitiva, Zubiri no admite que la conceptuación de la realidad matemática por construcción sea una axiomatismo formalista, pero esto no significa que se posicione en la escuela opuesta a ésta: el intuicionismo sobre todo de Brouwer. Por ello es preciso examinar a continuación su rechazo asimismo del constructivismo intuicionista.

 

3.3. Insuficiencia sentiente del constructivismo intuicionista de Brouwer.

Zubiri centra su estudio sobre todo en el intuicionismo[233] de Brouwer y Heyting, para delimitar su noción de construcción sentiente de la construcción intuicionista, y, a la vez, mostrar su insuficiencia y fundamentarla.

El intuicionismo se presenta como una escuela de filosofía de la matemática contrapuesta a la escuela "logicista" y a la escuela "formalista" , y como tal rechaza la tesis fundamental de éstas: que la matemática se funda en la lógica. Por el contrario, el intuicionismo de Brouwer y Heyting subordinan la lógica a la matemática. Consideran inadecuada la lógica clásica para las construcciones matemáticas; por ejemplo, afirman que el principio lógico del tertio excluso no es adecuado para la demostración matemática, y hacen una crítica del mismo. Heyting, en Intuitionism. An Introduction, pone en boca del personaje IN, en su disputa con interlocutores de otras escuelas de la matemática, la concepción intuicionista:

"IN: Debería usted tener en cuenta cuál era el programa de Brouwer [L.E.J. Brouwer 1907]: consistía en investigar las construcciones mentales matemáticas como tales (...). Y que este punto de vista conduce inmediatamente a rechazar el principio del tercio excluso es algo que como puedo mostrarlo mejor es con un ejemplo"[234]

A pesar de su extensión, reproducimos a continuación este sencillo y claro ejemplo, porque nos permite constatar, por un lado, su rechazo a admitir una prueba matemática que apele al principio lógico del tercio excluso, y, a la vez, el sentido intuicionista de construcción como operación ejecutada. Veamos lo que sigue diciendo IN:

"Comparemos dos definiciones de números naturales, k y l, por ejemplo.

I. k es el mayor número primo tal que k-1 sea también primo, y k =1 en caso de que no exista tal número.

II. l es el mayor número primo tal que l-2 sea también primo, y l =1 en caso de que no exista tal número.

La matemática clásica desdeña completamente la obvia diferencia de carácter entre estas dos definiciones; pues es posible calcular realmente k (k =3), mientras que no tenemos método alguno de calcular l, ya que no se sabe si la sucesión de pares de primos gemelos, p, p +2, es finita o no. De ahí que los intuicionistas rechacen II como definición de un entero: consideran que sólo está bien definido un número entero cuando se da un método para calcularlo; ahora bien, este modo de razonar lleva a rechazar el principio del tercio excluso, ya que si la sucesión de números primos gemelos fuese o finita o infinita, II definiría un entero"[235]

La matemática es concebida por el intuicionismo, no como un sistema de operaciones definidas o de definiciones axiomáticas, sino como un sistema de operaciones ejecutadas, esto es de operaciones compuestas de pasos finitos. No basta con definir, hay que "contar lo dado’, "operar". "Existir" en el sentido de las construcciones mentales matemáticas, tal y como lo entiende Brouwer y Heyting, es sinónimo de "haberse construido".[236] Esto lleva a la consideración de que la matemática no es un saber sino más bien un hacer. Este criterio es el requisito para admitir o rechazar los resultados de la matemática clásica. El primer problema que plantea el constructivismo intuicionista es que su concepción supone la eliminación de una construcción matemática que exija una sucesión infinita de operaciones encadenadas. El constructivismo intuicionista reduce la matemática a una parcela. Precisamente surge en gran parte como una reacción contra la teoría de los números transfinitos de Cantor. Zubiri constata tajantemente este carácter restrictivo del intuicionismo.

"El objeto de la matemática serían, pues los conjuntos finitos como término de operaciones ejecutadas sobre ellos. El intuicionismo es radicalmente un finitismo"[237]

Sin embargo, el infinito actual es base de muchos desarrollos de la matemática moderna, por ejemplo, el análisis infinitesimal, por ello la mayoría de los matemáticos no estaban dispuestos a renunciar a ello y rechazaron la postura intuicionista de Brouwer. Hacemos un inciso para constatar que Zubiri llama la atención sobre este carácter finitista del constructivismo intuicionista, si bien como su objeto de análisis en este momento es ver el carácter de construcción de las operaciones ejecutadas, tiene que apartarlo, como él dice: "Pero no nos ocupemos de este aspecto de la cuestión...". El tema del infinito actual a Zubiri le preocupa, y constata de forma negativa que la postura intuicionista conduce a un finitismo. Esto nos hace pensar que su constructivismo sentiente de la matemática irá más lejos que el intuicionismo, y pretenderá dar cuenta del infinito actual como una construcción sentiente. También nosotros dejamos pendiente para más adelante, el análisis de si el constructivismo sentiente es un infinitismo. Pero nos interesaba, como hace Zubiri, apuntar en este contexto el problema del infinito actual, para ver una de las objeciones matemáticas al intuicionismo.

Además, desde el punto de vista filosófico, esta conceptuación intuicionista es insostenible, para Zubiri, por dos razones que analizaremos: 1. Los conjuntos a pesar de ser finitos no son intuitivos, y 2. La construcción por operaciones ejecutadas es insuficiente.

"ni los conjuntos — por finitos que sean— son formalmente intuitivos, ni las operaciones ejecutadas sobre ellos constituyen lo radical de lo que yo entiendo por construcción matemática"[238]

1. ¿Por qué dice Zubiri que el conjunto finito de Brouwer no es intuitivo? La intuición nos da de forma inmediata, directa y unitaria (son los caracteres de la intelección intuitiva) no un conjunto sino que primariamente nos da una unidad de momentos. Por tanto, la intuición nos da "diversidad de momentos", no así un "conjunto de elementos", como supone Brouwer. El conjunto no es un "dato", es una construcción ulterior a la intuición de la diversidad. En palabras de Zubiri:

"Porque la intuición no da sino ‘diversidad de momentos’, pero jamás nos da ‘conjunto de elementos’. Para tener un conjunto es necesario un acto ulterior de intelección que haga de los momentos elementos. Hace falta pues una construcción" [239]

Construimos el conjunto aislando los momentos de la intuición y constituyéndolos en elementos, y se lo aplicamos a la diversidad de lo dado. De ahí que Zubiri, con su agudo sentido crítico, diga que no es exacta la denominación de intuicionismo referida a la matemática de Brouwer.

"El llamado conjunto finito, presuntamente dado en la intuición, no es sino la aplicación del conjunto ya construido intelectivamente a la diversidad de lo dado. Esta aplicación es justo una postulación: se postula que lo dado se resuelve en un conjunto. Por consiguiente, en estricto rigor no puede llamarse intuicionismo a la matemática de Brouwer. El conjunto de Brouwer no es intuitivo; es el contenido objetivo de un concepto de conjunto que se "aplica" a lo intuitivo"[240]

En este sentido esta postura se aproxima a la construcción kantiana. De hecho, Kant es un antecedente del intuicionismo. Lo que Brouwer toma como intuición es una construcción, y esto confirma la tesis de Zubiri de que el objeto matemático del mismo modo que no es concepto, no es tampoco intuición, sino que es construcción sentiente.

2. Una vez asentado que la noción de conjunto de Brouwer no es intuitiva sino que es una construcción, nos planeamos la segunda cuestión pendiente: ¿Por qué la construcción del conjunto no es radicalmente un sistema de operaciones ejecutadas? Cierto que Brouwer considera las operaciones ejecutadas como el modo de construcción apropiado para obtener la matemática libre de paradojas. Zubiri muestra la insuficiencia de la construcción de las operaciones ejecutadas para fundamentar la matemática. Y esto es así porque partimos del conjunto finito como contenido de conceptos objetivos. Por ello, las operaciones ejecutadas sobre este contenido son todo lo ejecutadas que queramos, pero igualmente conceptivas en cuanto que no salimos del concepto objetivo del que partimos. De este modo la matemática no sería ciencia de realidad, sino que se movería en el plano de los conceptos. Transcribimos seguidamente un texto de Zubiri de una importancia capital.

"Finitos o no, los conjuntos de que se ocupa la matemática de Brouwer y las operaciones sobre ellos ejecutadas son conjuntos y operaciones conceptivas. Y por esto no son suficientes, a mi modo de ver, para fundamentar lo matemático: la matemática no trata de ‘conceptos objetivos’ sino de ‘cosas que son así’. Lo que yo entiendo por construcción es algo distinto.’"[241]

Este texto nos parece revelador de lo que constituye el nervio de nuestra tesis: la fundamentación de lo matemático constituye un auténtico problema para Zubiri. Él mismo ha experienciado la insuficiencia del constructivismo intuicionista para acometer esta tarea, lo mismo que la del axiomatismo formalista. Zubiri va a tratar de colmar el vacío que existe en la fundamentación matemática. Su diálogo con las distintas escuelas de la fundamentación de la matemática, le permite concluir que la raíz de la insuficiencia de todo intento de fundamentación de lo matemático está en la vía conceptiva emprendida y que sólo puede conducir a una matemática de "conceptos objetivos", pero no a una matemática de "entes matemáticos". Para ello hay que marchar por otra vía sentiente. Por ella nos echa a andar su constructivismo sentiente.

En efecto, Zubiri constata que tanto la matemática de Brouwer como la matemática de Gödel y de Cohen, son construcción concipiente de la matemática,

"Lo que yo entiendo por construcción es algo distinto. Ciertamente no es una construcción de conceptos objetivos por mera definición, pero tampoco es una serie de operaciones ejecutadas en el sentido de Brouwer, porque estas operaciones de Brouwer repito son operaciones sobre conceptos objetivos. Y en este punto la matemática de Brouwer no difiere de la de Gödel y Cohen" [242]

Zubiri ofrece claramente su constructivismo sentiente como una filosofía de la matemática radical en contraposición al conceptismo del intuicionismo de Brouwer (antes lo hemos visto respecto del axiomatismo formalista). Nos dice el autor:

"A lo que yo me refiero es a que construir no es ejecutar operaciones objetivas sino proyectar ante mi inteligencia ese contenido objetivo en "la" realidad física. Y esta realidad no está dada en intuición sino en aprehensión primordial de realidad; está dada impresivamente. Como esta realidad no tiene contenido determinado yo puedo proyectar libremente sobre ella el contenido de lo objetivamente construido operacionalmente. Esta proyección y no la operación es la construcción matemática"[243]

Desde la inteligencia sentiente, el resultado del análisis zubiriano de la concepción intuicionista de Brouwer es que su noción de conjunto finito no es intuitiva sino que se debe a una doble postulación: 1. la posibilidad de aplicar lo dado en la intuición a un conjunto de elementos. 2. la proyección en "la" realidad como contenido suyo del conjunto construido operacionalmente. Esto sólo es posible en inteligencia sentiente. Una vez más es preciso colocarse en la vía de intelección sentiente para fundamentar las distintas escuelas de filosofía de la matemática, abandonando la vía sensible o conceptiva.

 

3.3.1 Intuición: dimensión noética de la aprehensión primordial de realidad.

Como el término de aprehensión primordial de realidad es una aportación original de Zubiri, es fácil que nuestras mentes traten de asimilarlo al término tradicional en la filosofía de intuición. ¿Es correcta la ecuación entre intuición y aprehensión primordial de realidad? La cuestión es clave para evitar equívocos y precisar claramente la postura constructivista de Zubiri en la matemática. Nuestro autor repara en ello y llama enérgicamente la atención sobre la distinción que a su modo de ver existe entre ambos términos: intuición y aprehensión primordial. Su postura no es un intuicionismo sino que es un inteleccionismo sentiente o un sensismo intelectivo (usamos en esta ocasión esta expresión en lugar de constructivismo sentiente para hacer hincapié en el momento primario de aprehensión primordial de realidad sin la cual no se puede construir el objeto matemático). El objeto matemático es aprehendido en aprehensión primordial de realidad. En palabras de Zubiri:

"El objeto matemático no es intuido sino que es aprehendido en aprehensión primordial"[244].

Lo específico de la intuición no hay que buscarlo en la línea del objeto, puesto que autores como Ockam y Kant consideran que lo intuible es lo singular, mientras que Platón, Leibniz y Husserl piensan que hay intuición de lo no-sensible. Lo decisivo para caracterizar la intuición está, según Zubiri, en el modo de presencia del objeto. La intuición es la presencia de algo real a la intelección de modo inmediato, directo y unitario. Pues bien, estas notas de lo presente en la intuición las tiene también lo presente en la aprehensión primordial de realidad:

"En ella la formalidad de realidad está aprehendida directamente, no a través de representaciones o cosas semejantes. Está aprehendida inmediatamente, no en virtud de otros aspectos aprehensivos o de razonamientos del orden que fuere. Está aprehendida unitariamente"[245]

A pesar de estas notas comunes, según Zubiri, intuición y aprehensión primordial de realidad son cosas distintas. La aprehensión es un físico "estar" "con" la cosa y "en" la cosa, y en la que la cosa está "quedando" en la intelección. Este carácter físico de la aprehensión se opone al carácter intencional de la intuición. La aprehensión primordial frente a la intuición sugiere un carácter "táctil" más que "visual", y una asimilación más que una distancia; desde esta perspectiva, incluso lo visto tiene que ser aprehendido. La aprehensión es ergon o noergia. Por esto el noema y noesis, no son momentos intelectivos primarios. Dice Zubiri:

"La intuición no es sino dimensión noética de la aprehensión primordial de realidad. La aprehensión primordial de realidad es pues en sí misma mucho más que intuición: es una aprehensión noérgica. No es un ver sino un aprehender en impresión de realidad"[246]

El error de identificar la aprehensión primordial con la intuición está en tomar la aprehensión primordial como mero acto de conciencia; si así fuera, la aprehensión primordial sería la conciencia inmediata y directa de algo, esto es, intuición. Pero esto es equívoco ya que no se trata en la aprehensión de mera conciencia. La impresión no tiene que ver en primer lugar con la unidad noético-noemática sino que es un acto de aprehensión, y Zubiri lo denomina una noergia, un érgon[247].

Hecha esta distinción vemos que la realidad física está presente en la intelección por el acto de aprehensión primordial de realidad y no por la intuición, que no es sino su aspecto noético (un darse cuenta). Por ello dice Zubiri que el objeto matemático no es intuido sino aprehendido en la aprehensión primordial. En ésta se nos da la realidad en la cual construimos sentientemente el contenido matemático. Es la intelección sentiente y no la intuición el fundamento de la matemática. Por ello, frente al intuicionismo denominamos la aportación de Zubiri: inteleccionismo sentiente (en el momento radical y posibilitante de la construcción matemática) como vía última de fundamentación de la matemática.

Para concluir nuestro capítulo sobre la ultimidad del constructivismo sentiente sobre otros constructivismos y, por tanto, la radicalidad de la filosofía de la matemática de Zubiri y su carácter fundante de lo matemático, transcribimos a continuación un texto, a nuestro modo de ver, revelador de la conciencia que tiene nuestro filósofo de aportar una nuevo fundamento de lo matemático: la construcción sentiente, y de su carácter radical respecto de los otros modos "conceptivos" de entender la construcción matemática,

"Pues bien, construir es otra cosa; es crear, es proyectar libremente en "la" realidad física un contenido según conceptos. Postular es postular realidad. Sin esta construcción y postulación radical y primaria serían imposibles tanto los axiomas de Zermelo-Fraenkel y los conjuntos des Cohen como el intuicionismo de Brouwer.

La construcción matemática es siempre por tanto un acto de inteligencia sentiente"[248]

A este resultado hemos llegamos: intuicionismo y el axiomatismo formalista tienen en común que son filosofías "conceptivas" de la matemática y por tanto son insuficientes como fundamentación de la misma. Ambas precisan ser incardinadas en un fundamento común: la inteligencia sentiente, y ser desarrollos dentro de una filosofía sentiente de la matemática. En la línea de la formalidad no se oponen como sí ocurre desde la línea del contenido. Los contenidos de los conceptos matemáticos se han podido obtener por distintas vías (según las distintas "escuelas" de filosofía de la matemática: por construcción sensible, por intuición, por definición, por ejecución, etc.), sea como sea, estos conceptos no son el objeto matemático, porque si así fuera no tendríamos ciencia de realidad sino un mero sistema de conceptos. La construcción sentiente consiste, por el contrario, en realizar el contenido "según conceptos" en la formalidad de realidad impresivamente dada en aprehensión primordial. Es toda la diferencia entre una construcción sentiente y la meramente concipiente.

La firmeza con la que Zubiri expone el fundamento constructivo-sentiente de la matemática, es fruto de un profundo esfuerzo sostenido durante todo su discurrir filosófico. Desde que el Zubiri de la Teoría Fenomenológica del Juicio (1921) expresara el interés filosófico de la matemática y la tarea filosófica de fundamentar la matemática e interpretar sus resultados, hasta que el Zubiri de Inteligencia y Logos (1982) presenta una original fundamentación y concepción de la matemática, han pasado casi sesenta años. La firmeza de sus convicciones es el resultado de una búsqueda denodada.

---

NOTAS

[1] Método como vía en la realidad dada y no en la verdad.^

[2] Sin embargo, no tomamos la fenomenología como constitución de la objetividad, tal como la presenta su fundador Husserl, y que vemos que configura el momento en que Zubiri presenta su tesis doctoral T.F.J., sino que el término fenomenología es entendido como descripción de la realidad en su actualidad en la Inteligencia sentiente. El pensamiento original de Zubiri es netamente metafísico.^

[3] I.R, p. 183^

[4] T.F.J p. 48^

[5] I.R, p.94^

[6] Estas ideas están expuestas en el capítulo anterior, a él nos remitimos.^

[7] IS, p 224^

[8] "Respectividad de lo real", p.25^

[9] Cf. IR p. 315.^

[10] Cf. IS p.13^

[11] Respectividad de lo real, 25^

[12] Es una interpretación del texto de Zubiri I.S 65-67 llevado al campo de la matemática.^

[13] IS p. 87^

[14] IL p.137^

[15] Ante la pluralidad de términos ("constructismo", "construccionismo", "construccionalismo") para designar las corrientes filosóficas "en las que la noción de construcción —y la correlativa de ‘constitución’— desempeña un papel importante", hemos elegido la denominación de "constructivismo", siguiendo el criterio de Ferrater Mora, quien nos dice: "El término ‘constructivismo’ es preferible a ‘construccionismo’ y a ‘construccionalismo’, por derivar naturalmente del adjetivo ‘constructivo’, correspondiente al nombre ‘construcción’" (Diccionario de Filosofía). Zubiri utiliza la expresión "intelección constructiva" (IL p.104).^

[16] Cf. Kant, Crítica de la Razón Pura, B 741.^

[17] J. de Lorenzo, (1992), p. 163.^

[18] Como dice Camino Cañón (1993, p. 253): " La consideración de los objetos matemáticos como construcciones, dará lugar a una manera de hacer matemáticas denominada "constructivismo", aunque propiamente hablando, deberemos hablar de ‘constructivismos’".^

[19] I.L p.143^

[20] Por ello aunque en alguna ocasión digamos solamente construcción hay que entenderla como construcción sentiente. Es la inteligencia sentiente la que construye de un modo sentiente.^

[21] J. de Lorenzo (1974), p. 3, 356-57.^

[22] IL p.131.^

[23] I.L p.145^

[24] H.D p.192^

[25] En su obra Hombre y Dios, p. 204, dice Zubiri: "Donación-entrega es la estructura metafísica de la causalidad interpersonal entre Dios y el hombre en la tensión teologal de su vida". Creemos que es también la estructura de la causalidad respectiva entre la realidad y la inteligencia sentiente, en la tensión intelectiva del hombre.^

[26] IL p.95^

[27] I.L p.145^

[28] IL 145, el subrayado es nuestro.^

[29] IL p.249, el subrayado es nuestro.^

[30] Véase EDR.^

[31] IL p.134^

[32] IL p.265 subrayado nuestro^

[33] IL p.144 subrayado nuestro^

[34] IL p. 50^

[35] IS p.12. (subrayado nuestro)^

[36] IR p.87 (subrayado nuestro)^

[37] IL p.145 (subrayado nuestro)^

[38] IL p. 50 (subrayado nuestro)^

[39] IL p.51 (subrayado nuestro)^

[40] IL p.52 (subrayado nuestro)^

[41] IL p.143 (subrayado nuestro)^

[42] IL p.145^

[43] IS p.31-32^

[44] IL p.122 subrayado nuestro^

[45] IR p.272 subrayado nuestro^

[46] IS p.60-61^

[47] IS p.33 subrayado nuestro^

[48] IS p.45^

[49] En inglés: forcing.^

[50] IL p.137^

[51] IL p.133 ^

[52] IL p.132 subrayado nuestro^

[53] Cfr. IR p.86.^

[54] Véase libro II del Sistema de Lógica^

[55] Seguidores actuales son los filósofos de la matemática Ph. Kitcher, M. Kline, R.L. Wilder.^

[56] J.S. Mill (1843) II, v, 1 A system of Logic. New York: Longmans (1936), trad. esp. Sistema de lógica inductiva y deductiva. D. Jorro, (ed) Madrid, 1917. Trad. cast. E. Ovejero.^

[57] Ibid II, v, 1.^

[58] Ibid, II, v. 2.^

[59] Ibid, II, v. 4^

[60] Véase C. Cañón, (1993) p. 188.^

[61] IR p.88-9^

[62] IR p.89^

[63] IR p.251^

[64] IR p.251^

[65] IR p.212^

[66] Véase Feyerabend, "Una lanza por Aristóteles. Anotaciones al postulado del aumento del contenido", en Progreso y racionalidad en la ciencia.^

[67] Ibid. p.141.^

[68] Ibid, p.142^

[69] IR.p.42^

[70] IR p.130.^

[71] IR p.131^

[72] IR p.131^

[73] IS ,p.87^

[74] Zubiri nos dice que es la propia evolución de la ciencia, que comenzó con Einstein y llega a su grado máximo con la mecánica cuántica, la que nos lleva a la subordinación de la teoría a la experiencia. Ambos momentos se pertenecen, de ahí la creación de conceptos experimentales, traducibles en experiencias conceptuales. Zubiri entiende por conceptos experimentales, no aquellos que están de acuerdo con la experiencia, como si la experiencia fuera algo exterior a ellos y se limitara a sugerirlos, aprobarlos o rechazarlos: "en el concepto experimental, la experiencia es ella misma un momento del concepto en cuanto tal". En la nueva física, los conceptos son la experiencia misma hecha concepto. El sentido del concepto físico es ser en sí mismo una experiencia virtual. Recíprocamente, la experiencia tiene en sí una estructura conceptual (cfr. NHD 331). Veremos que la experiencia, tal como la entiende Zubiri, es también método de la matemática, y en este sentido lo dicho de la física tiene su aplicación a la matemática. ^

[75] IL p.101^

[76] IL p.103^

[77] IL p.104^

[78] IL p.104 subrayado nuestro^

[79] IL p.104^

[80] IL p.104^

[81] IL p.131, subrayado nuestro^

[82] IL p.138^

[83] IR p.129^

[84] IR p.130^

[85] IR p.128^

[86] IR p.130^

[87] IR p.128^

[88] A. Ferraz, El espacio en la metafísica de Zubiri, p. 79^

[89] I.Ellacuría, El espacio, p. 482^

[90] A. Ferraz, art. cit. p. 81^

[91] I. Ellacuría, art. cit. p. 484^

[92] IR p.130^

[93] IR p.130^

[94] Hasta 1800 aproximadamente el espacio matemático era una idealización del espacio físico. La geometría euclídea se mostraba evidente y de ahí los intentos en fundamentar otra áreas de la matemática (álgebra, la aritmética y el análisis) en ella. En la filosofía, Kant consagró el carácter absoluto de la geometría euclideana. El espacio es una forma "a priori" de la sensibilidad del sujeto y sus caracteres son inmutables. Sin embargo, el V Postulado de la geometría euclidea no gozó nunca del carácter autoevidente de los demás postulados. Se trató de demostrar que se derivaba del resto de axiomas o de sustituirlo por otro axioma más adecuado. En 1759 D´Alembert llamó a este problema: " el escándalo de los elementos de la geometría" Después del esfuerzo de grandes matemáticos, Gauss, Lobatchevsky y Bolyai concluyeron que el axioma de las paralelas no puede deducirse del resto, era independiente y cambiando éste por otro resultarían geometrías no-euclideas. Esto supuso una auténtica conmoción. El filósofo más profundo de la geometría fue Riemann, en 1854 pronunció la conferencia " Sobre las hipótesis en que se funda la geometría" que se publicó en 1868. Riemann estudió la cuestión de la certeza del conocimiento del espacio físico. Uno de sus objetivos era mostrar que los axiomas de Euclides no eran autoevidentes sino empíricos.^

[95] IR p.131^

[96] IR p.130^

[97] IR p.131^

[98] IR p.131^

[99] IR p.131.^

[100] "Geometría e intuición", 1954, en Matemáticas en el mundo moderno Kline, p. 212.^

[101] "El concepto descriptivo del tiempo" (1974-5) p.16 ^

[102] IR p.132-3^

[103] IR p.125^

[104] IR p.127^

[105] IR p.128^

[106] IR p.129^

[107] EDR p.36^

[108] IL p.326^

[109] IL p.326-7^

[110] I. Ellacuría, art. cit. p.483^

[111] A. Ferraz, art. cit. p.82^

[112] IR 113^

[113] IR 113^

[114] SE 356 ^

[115] IR p.113^

[116] IL p.161 ^

[117] IR p.114^

[118] SE p.355-356^

[119] IR p.114^

[120] SE p.320^

[121] IL p.130^

[122] IL p.131^

[123] IL p.129^

[124] IR p.130^

[125] En el juicio, realizar es proyectar o aplicar una simple aprehensión (percepto, ficto o concepto) en "la" realidad de la cosa ya aprehendida. De este modo, ésta queda actualizada campalmente, no sólo como real sino en su contenido "en realidad".^

[126] IL p.149^

[127] IL p.164-5^

[128] IR p.205^

[129] IR. p.254^

[130] IR p.206^

[131] IR p.207^

[132] Cfr. Tarski, opus cit. p. 149 ss.^

[133] IR p.207^

[134] IR p. 254^

[135] IR p.252^

[136] IR p.253^

[137] IR p.208, subrayado nuestro.^

[138] IR p.253^

[139] IR p.208^

[140] IR p.209^

[141] IR p.209^

[142] IR p.253^

[143] Cfr. IL p.328^

[144] IR p. 251^

[145] IR p. 251^

[146] IR p.251^

[147] Cfr. IR p.148^

[148] IR 220-1^

[149] IR p.141^

[150] IR p.141^

[151] IR p.144^

[152] I. Ellacuría, El Espacio, p.483^

[153] A. Ferraz, El espacio en la metafísica de Zubiri. p.82-3^

[154] SE p.66^

[155] IR p.224^

[156] IR p.226-7^

[157] IR p.227^

[158] IR p.227^

[159] IR, p.253-4^

[160] IR p.254^

[161] NHD p.68^

[162] Ibid, p.69^

[163] Ibid, p.71^

[164] Ibid, p.74^

[165] IR p.254^

[166] Desde los años treinta el panorama viene determinado por la discusión crítica entre el Falsacionismo de Popper y el Empirismo Lógico. Desde los años 60, los métodos y conclusiones del empirismo lógico y del falsacionismo han sido objeto de ataque sostenido por varios autores de antecedentes filosóficos diversos: Hanson, Polanyi, Toulmin, Kuhn, Feyerabend. En contraste con el empirismo lógico, el rasgo más destacado del nuevo enfoque es el rechazo de la lógica formal como herramienta principal del análisis de la ciencia, y su sustitución por la confianza en el estudio de la historia de la ciencia. Lakatos buscó establecer una posición intermedia: quiso trasladar a un terreno objetivo las visiones histórico-científicas de Kuhn.^

[167] Popper también identifica lo lógico con lo racional y niega de este modo que el descubrimiento científico sea racional. "No hay un método lógico para tener nuevas ideas, o una reconstrucción lógica de este proceso. Cada descubrimiento contiene un elemento irracional", o una "intuición creativa".^

[168] véase Brown, La nueva filosofía de la ciencia^

[169] IR p.216^

[170] IR p.216^

[171] IR p.216^

[172] IR p.214-5^

[173] Brunschvicg, o.c., p.287^

[174] Crítica de la Razón pura, B 19-20^

[175] Brunschvicg, o.c p.601.^

[176] Crítica de la Razón pura, B 16-7^

[177] Ibid, B 189-190^

[178] Ibib, B 752^

[179] Ibid, B, 750^

[180] Ibid, B 15 ^

[181] Ibid, B 16^

[182] I.L p.247^

[183] Kant, o.c. B 75-6^

[184] I.L p.248^

[185] IL p.249^

[186] IL p.249^

[187] IL p. 249^

[188] IL p.250^

[189] IL p.251^

[190] Ibid. p.247^

[191] Ibid p.251^

[192] Crítica de la Razón pura, B 15^

[193] Ibid, B 15^

[194] Ibid, B 15-6^

[195] Ibid, B 16^

[196] TFJ p.166^

[197] TFJ p.167^

[198] El Zubiri maduro no hará la distinción entre sentidos y entendimiento.^

[199] TFJ p.187^

[200] TFJ p.188^

[201] Véase en el punto 3 del capítulo I, la superación de la descripción predicativa por la descripción funcional.^

[202] IL p.221^

[203] IL p.247^

[204] IL p.218^

[205] C.l.f. p. 87^

[206] C.l.f. p. 87^

[207] C.l.f. p. 89^

[208] Crítica de la Razón Pura, B 154-5^

[209] Zubiri, en "la idea de naturaleza: la nueva física" (1934), recogido en Naturaleza, Historia, Dios , pp. 293- 353, se plantea el problema de la unidad de la física: la del macrocosmos (continuista) y la del microcosmos (discontinuista). Afirma al respecto: "No puede haber dos físicas, porque hay una sola Naturaleza, la cual, o da saltos, o no los da" (p. 299). Y un poco más adelante: "En la crisis que a la nueva física se plantea, cualquiera que sea su solución, no se trata de un problema interno a la física ni de un problema de lógica o teoría del conocimiento físico: se trata, en última instancia, de un problema de ontología de la Naturaleza". (p. 351). A Zubiri no le resulta satisfactorio ningún tipo de solución dualista y busca una ultimidad en la nociones de las ciencias que permita dar razón de todo cuanto hay en ellas. Paralelamente, en el campo matemático, el problema está en determinar cuál es la naturaleza de la realidad matemática, porque no puede ser que unos objetos sean sensibles y otros lógicos. Sospechamos que este sería el objeto de reflexión que haría Zubiri en la intervención que tuvo en el año 1946, en la Universidad de Princeton, de la cual sólo parece que se conserva el título: "le reel et les mathematiques: un probleme de philosophie".^

[210] J. de Lorenzo, 1992, pp.176-7^

[211] Ibid, p. 177^

[212] Ibid, p. 176^

[213] J. de Lorenzo, o.c p.167^

[214] IL p.143^

[215] En el concepto de función (c. I, punto 3), indicamos que Russell posiblemente influye en Zubiri. Ambos tienen un enfoque funcional de la Matemática.^

[216] Crítica de la Razón Pura, B 753^

[217] Ibid, B 743-4^

[218] Ibid B 754-5^

[219] Ibid B 757-8^

[220] Ibid p.761^

[221] Cfr. Crítica de la Razón pura, B 763^

[222] Ibid. B 762^

[223] Ibid B 764^

[224] SH p.153-4^

[225] IS pp.129-30^

[226] EDR pp.243-4^

[227] Cfr. EDR 244^

[228] IR p.284^

[229] EDR p.244^

[230] EDR pp.244-5^

[231] IL p.137^

[232] IL p.138^

[233] El intuicionismo, que se inspira en Kant, se presenta en la actualidad como: a) Semi-intuicionismo de la escuela de París: R. Baire, E. Borel, J. Hadamard, H. Lebesgue, y H. Poincaré. Se limitan a criticar el logicismo, cantorismo y formalismo, pero sin elaborar una construcción de las matemáticas. b) Intuicionismo radical de Brouwer y Heyting.^

[234] Heyting, Introducción al intuicionismo, trad. cast., 1976, p. 13^

[235] Ibid, pp. 13-4^

[236] Ibid, p.14^

[237] IL p.140^

[238] Ibid. p.140^

[239] Ibid. p.140^

[240] Ibid p.141^

[241] Ibid pp.141-2^

[242] IL p.142^

[243] IL p.142^

[244] IL p.142^

[245] IS pp.64-5^

[246] IL p.242^

[247] Cfr. I.S p.67^

[248] IL p.143^